Экспериментальная проверка распределения Максвелла

Границы применимости распределения Максвелла

При достаточно низких температурах классическое приближение при описании газов непригодно, т.е. для них становятся существенными квантовые эффекты. Оценим эти температуры для различных газов.

По законам квантовой механики любая физическая система, в частности частица, не может находиться в состояниях, в которых координаты её центра инерции и импульс одновременно принимают вполне определённые, точные значения – принцип неопределённости Гейзенберга.

Выделим в газе маленький кубик со сторонами , , 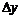, 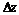на который в среднем приходится одна частица. Исходя из принципа неопределённости (без учёта численных коэффициентов порядка единицы), можно заключить, что если выполнены условия » 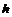, » 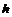, » 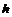, то движение частицы в этом кубике можно рассматривать классически. Здесь 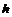– постоянная Планка 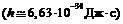. Действительно, согласно принципу неопределённости Гейзенберга, произведение квантовых неопределённостей координаты и импульса частицы порядка 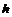, а потому при соблюдении указанных условий эти неопределённости существенной роли не играют.

Отсюда » , где – объём кубика, – некоторый средний импульс, характеризующий движение частиц газа. Или «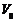, «, «, где – концентрация частиц. Запишем в виде: «, где 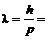– длина волны де-Бройля (микрочастицы можно рассматривать как волны с определённой длиной).

Если взять для оценки , то последнее условие примет вид:

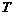» , где – температура вырождения газа.

Следовательно, классический способ рассмотрения применим при температурах, значительно превышающих температуру вырождения.

Газы ниже температуры вырождения называются вырожденными. К ним классический способ рассмотрения не применим.

Для обычных атомных и молекулярных газов близка к абсолютному нулю (например, для температура вырождения ~ ). Для всех остальных газов (за исключением водорода) ещё ниже, чем для гелия. Поэтому к таким газам в температурной области их существования (до температуры сжижения) практически всегда применимо классическое рассмотрение.

Для электронного газа в металлах ~ , т.е. функция распределения Максвелла неприменима.

Таким образом, для реальных газов вследствие того, что массы частиц достаточно большие, квантовые эффекты начинают сказываться лишь при очень низких температурах. Если рассматривать электронный газ в металле, то квантовые эффекты уже существенны при комнатной температуре. Поэтому электронный газ мы описываем только с помощью квантовой механики, а реальные газы описываем классически (для комнатных температур, например), тогда можно разделить пространственные и импульсные координаты частиц.

 

 

Экспериментальная проверка распределения Максвелла

 

В ряде способов проверки закона распределения Максвелла используются молекулярные пучки, которые получают путём выделения в вакуумной камере пучка молекул, испаряющихся из нагреваемого вещества. Наличие высокого вакуума в камере необходимо для предотвращения столкновений между молекулами исследуемого вещества и воздуха. Рассмотрим два таких способа.

Первый опыт по непосредственному измерению скоростей молекул осуществил в 1920 г. немецкий физик О. Штерн. Два коаксиальных цилиндра радиусами R и r приводились во вращение с одинаковой угловой скоростью w вокруг вертикальной оси, на которой находилась платиновая

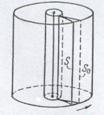
нить, покрытая слоем серебра (рис.). При нагревании нити электрическим током серебро испарялось, и его атомы летели во все стороны. Узкая продольная щель во внутреннем цилиндре позволяла узкому пучку атомов (молекулярному пучку) выйти в пространство между цилиндрами, где, как и во всём приборе, был создан вакуум. При неподвижных цилиндрах атомы серебра оседали по линии S 0. При вращении цилиндров след атомов должен был сместиться против направления вращения цилиндров, так как за время прохождения атомом серебра (скорость ) отрезка цилиндры поворачивались на угол , определяемый соотношением .

 

Оказалось, что смещение действительно имеет место, причём след расплывается. Это объясняется тем, что атомы имеют разные скорости.

Более точно закон распределения был проверен в опыте Ламмерта (1929г.), в котором молекулярный пучок пропускался через два вращающихся диска с радиальными щелями, смещёнными друг относительно друга на некоторый угол (рис.).

 

 

При угловой скорости 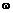диски повернутся на угол в течение времени . Поэтому через обе щели пройдут молекулы со скоростями , где – расстояние между дисками. Из-за конечной ширины щелей прибор выделяет молекулы, скорости которых лежат в пределах некоторого интервала .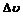

Меняя скорость вращения дисков 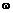, можно выделять из пучка молекулы, обладающие различными значениями скорости. Улавливая затем эти молекулы в течение определённого времени, можно определить их относительное количество в пучке. Так, в случае исследования пучка атомов легкоплавкого металла, газ из которых образован в камере при нагревании в результате испарения, эти атомы можно осаждать на экран и по толщине осаждённого слоя судить об их числе.

После пересчёта распределения скоростей в молекулярном пучке на распределение скоростей в изотропных условиях получают ступенчатую

гистограмму, которая при уменьшении величины интервалов 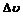стремится к некоторой плавной кривой (рис.). Эта кривая является изображением теоретически полученной Максвеллом функции распределения молекул по скоростям.

 

В другом методе измерения скоростей используется эффект Допплера. Когда молекула, в состоянии покоя излучающая свет некоторой частоты , движется в направлении к наблюдателю с относительной скоростью , частота света, принимаемого наблюдателем, равна , т.е. смещена в сторону высоких частот. При движении молекулы в противоположном направлении соответствующий коэффициент равен .

Эксперименты с газоразрядными источниками света показывают, что в спектре излучения светящегося газа присутствует не только основная частота , но и все другие частоты, получающиеся из вследствие эффекта Допплера, вызванного движением молекул. При этом интенсивность излучения на определённой частоте пропорциональна числу молекул, имеющих одно и то же значение компоненты скорости в направлении к наблюдателю. Поэтому каждая спектральная линия имеет конечную ширину, а распределение интенсивности в пределах одной линии непосредственно иллюстрирует максвеллово распределение.

 

Рассеяние атмосферы планет

 

Потенциальная энергия частицы в поле тяготения планеты:

.

Тогда , где – радиус планеты.

При концентрация .

Формула получена в предположении равновесного состояния атмосферы планеты и, в соответствии с ней, так как 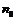имеет конечное значение, то и 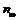будет иметь конечное значение. Но это невозможно, поскольку общее количество молекул в атмосфере планеты конечно, а объём пространства, окружающего её, бесконечно велик. Т.о. равновесие возможно только при , т.е. при полном отсутствии атмосферы.

Поскольку в конечном счёте все системы стремятся к равновесному состоянию, атмосфера планет постепенно рассеивается (очень длительный процесс).

У некоторых из небесных тел, например, у Луны, атмосфера полностью исчезла, другие, например Марс, имеют очень разреженную атмосферу. Т.е. атмосфера Марса находится близко к достижению равновесного состояния. У Венеры атмосфера очень плотная и, следовательно, находится в начале пути к равновесному состоянию.

 

Скорость звука в газах

 

В механике выводится следующая формула для скорости распространения звука в газах:

,

где – плотность газа.

Колебания плотности и связанные с ними колебания температуры в звуковой волне происходят настолько быстро, а теплопроводность газа настолько мала, что для таких процессов теплообмен не играет никакой роли. Разности температур между сжатиями (сгущениями) и разрежениями газа в звуковой волне не успевают выравниваться за период, так что распространение звука можно считать адиабатическим процессом.

Уравнение адиабаты:

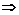
или , т.е.

, тогда .

Таким образом, – формула Лапласа.

По этой формуле при Т =273 К скорость звука в воздухе 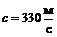, что совпадает с экспериментом.

Скорость звука в газах растёт с ростом температуры и давления, кроме того, в некоторых случаях она зависит от частоты звуковой волны.

Скорость звука в газах меньше, чем в жидкостях, а в жидкостях меньше, как правило, чем в твёрдых телах, поэтому при сжижении газа она возрастает.

 

Уравнение Бернулли

 

Обобщим уравнение Бернулли на движение сжимаемых жидкостей. Газ можно считать частным случаем сжимаемой жидкости.

Будем рассматривать адиабатическое ламинарное течение жидкости (по отношению к любой движущейся части жидкости окружающая жидкость играет роль адиабатической оболочки).

Запишем уравнение Бернулли: ,

где – полная энергия единицы массы жидкости (удельная энергия).

С учётом сжимаемости жидкости (газа) в выражение для должна входить удельная внутренняя энергия :

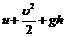
Тогда .

По определению, энтальпия 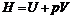, поэтому – удельная энтальпия (так как величина равна удельному объёму жидкости).

Таким образом, можно записать уравнение Бернулли в форме:

.

Если течение происходит в горизонтальном направлении, то величина остаётся постоянной, т.е.

При медленных течениях можно пренебречь кинетической энергией, тогда 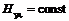, т.е. энтальпия вдоль линии тока остаётся постоянной.

Вычислим скорость истечения сжатого газа из баллона через малое отверстие или сопло (рис.):

Величиной можно пренебречь. Тогда

Если газ – идеальный, то .

Следовательно, .

Выразив из уравнения адиабаты ,

получаем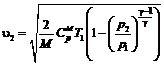

Максимальная скорость достигается при истечении в вакуум :

.

Поэтому в ракетной технике выгодно применять горючее с малой молярной массой, обладающее большой теплотой сгорания (чтобы температура была возможно выше).