Вектор, виды векторов. Операции над векторами. Системы векторов. Линейная независимость векторов. Базис. Скалярное произведение векторов и его свойства. N -мерное линейное векторное пространство. Линейные операторы. Матрицы. Операции над матрицами. Определители и их свойства. Ранг матрицы. Обратная матрица. Комплексные числа и многочлены. Собственные числа и векторы линейных операторов и матриц. Евклидово пространство. Квадратичные формы.
Тема 12. Элементы аналитической геометрии на прямой, плоскости и в трехмерном пространстве.
Уравнение линии. Прямая линия на плоскости и в пространстве: формы записи уравнений прямой. Уравнение плоскости. Угол между двумя прямыми, прямой и плоскостью, двумя плоскостями. Условия параллельности и перпендикулярности прямых, прямой и плоскости, плоскостей. Расстояние от точки до прямой. Линии второго порядка: эллипс, гипербола, парабола. Их канонические уравнения и графики.
Тема 13. Системы линейных алгебраических уравнений.
Решение системы уравнений. Векторная запись системы линейных алгебраических уравнений. Критерий совместности и число решений. Методы решения системы линейных алгебраических уравнений: метод Гаусса, формулы Крамера.
Тема 14. Основы математического программирования.
Системы линейных неравенств. Линейные задачи оптимизации. Основные определения и задачи линейного программирования. Симплексный метод. Теория двойственности. Дискретное программирование: постановка задачи и метод решения. Динамическое программирование: постановка задачи и метод решения. Нелинейное программирование: общая постановка задачи, классификация задач, метод множителей Лагранжа, поиск решения при безусловной оптимизации.
Раздел III. Теория вероятностей
Тема 15. События и их вероятности.
Сущность и условия применимости теории вероятностей. Основные понятия теории вероятностей: случайные события и их классификация, различные определения вероятности случайного события. Вероятностное пространство. Элементы комбинаторики. Основные теоремы о сложении и умножении вероятностей. Гипотезы. Формула полной вероятности и формула Байеса. Серии испытаний: схема и формула Бернулли, формула Пуассона. Простейший поток событий.
Тема 16. Случайные величины и способы их описания.
Дискретные случайные величины. Закон распределения. Числовые характеристики (математическое ожидание, дисперсия и среднее квадратическое отклонение). Непрерывные случайные величины. Функция и плотность распределения, их свойства. Числовые характеристики и их свойства. Модели законов распределения вероятностей случайных величин, наиболее употребляемые в социально-экономических приложениях. Закон распределения вероятностей для функций от известных случайных величин.
Тема 17. Закон больших чисел.
Локальная и интегральная теоремы Лапласа. Неравенство Чебышева. Закон больших чисел и его следствие. Особая роль нормального распределения: центральная предельная теорема.
Тема 18. Цепи Маркова.
Понятие цепи Маркова. Характеристики цепи Маркова. Использование цепей Маркова в моделировании социально-экономических процессов.
Тема 19. Элементы математической статистики.
Генеральная и выборочная совокупности, их среднее и дисперсия. Статистическое оценивание. Элементы дисперсионного анализа. Проверка статистических гипотез. Статистические методы обработки экспериментальных данных.
КОНТРОЛЬНАЯ РАБОТА
Вариант контрольной работы по математике содержит 11 заданий. Номера задач своего варианта контрольной работы студент должен выбирать последовательно в соответствии с буквами своих фамилии, имени и отчества согласно таблице выбора варианта, приведенной ниже:
Таблица выбора варианта
| Буквы фамилии, имени, отчества | Номера задач варианта контрольной работы | ||||||||||
| А, Б, В | |||||||||||
| Г, Д, Е, Ё | |||||||||||
| Ж, З, И, Й | |||||||||||
| К | |||||||||||
| Л, М | |||||||||||
| Н, О | |||||||||||
| П, Р | |||||||||||
| С, Т, У | |||||||||||
| Ф, Х, Ц, Ч | |||||||||||
| Ш, Щ, Ы, Ь, Ъ, Э, Ю, Я |
Например, студент Ильин Петр Алексеевич. Первая буква – “И”. Смотрим строку таблицы для буквы “И”. В столбце “1” для этой строки стоит число “3”, значит в первом задании студент П.А. Ильин должен решить задачу № 3. Вторая буква – “Л”. Смотрим строку таблицы для буквы “Л”. На пересечении столбца “2” и этой строки стоит число “15”, значит номер задачи из второго задания, соответствующий варианту данного студента – № 15 и т.д.
В результате выбора получим, что вариант контрольной работы студента Ильина П.А. содержит следующие номера задач: 3, 15, 30, 33, 46, 57, 62, 78, 89, 91, 105.
Варианты контрольной работы
Задание 1. Заданы два множества А и В (см. табл. 1). Определить множества А Υ В; А I В; А \ В; В \ А.
Т а б л и ц а 1
| Номер задачи | Множество А | Множество В |
| {1; 5; 7; 11} | {5; 9; 11; 15} | |
| {1; 3; 5; 7; 11} | {3; 5; 9} | |
| {2; 4; 6; 8} | {1; 2; 3; 4} | |
| {2; 6; 10; 14} | {4; 6; 10; 12} | |
| {0; 4; 8; 12} | {4; 8; 12; 16} | |
| {1; 3; 7; 9} | {3; 5; 9; 15; 23} | |
| {2; 4; 8; 12} | {4; 6; 8} | |
| {1; 5; 9; 11} | {2; 3; 4; 5; 6} | |
| {2; 4; 8; 16} | {3; 4; 8; 10; 20} | |
| {1; 3; 6; 10} | {3; 4; 5; 6} |
Задание 2. По данным промежуткам X Υ Y; X I Y; X и Y (см. табл. 2) определить X \ Y; Y \ X.
Т а б л и ц а 2
| Номер задачи | Х | Y |
| (0; 2) | [1; 4] | |
| (0; 3) | (3; 5) | |
| (0; 3) | (1; 4] | |
| [0; 2) | [1; +) | |
| [2; +) | (1; 5] | |
| (-3; -1] | [-2; 1) | |
| [-4; -1) | (-; -2] | |
| (-; 0] | (-1; +) | |
| [-1; 1] | (0; 10) | |
| (-2; 2] | [-2; 3] |
Задание 3. Решить, пользуясь формулами Крамера и методом Гаусса, систему линейных алгебраических уравнений (см. табл. 3):
Т а б л и ц а 3
| Номер задания | Система уравнений | Номер задания | Система уравнений |
 
|  
| ||
 
|  
| ||
 
|  
| ||
 
|  
| ||
 
|  
|
Задание 4. Даны координаты вершин треугольника АВС (см. табл. 4). Найти: а) длину стороны АВ; б) внутренний угол А в радианах с точностью до двух знаков после запятой; в) уравнения медианы СМ и высоты СК; г) площадь треугольника. Сделать чертеж.
Т а б л и ц а 4
| Номер задачи | А | В | С |
| (-8; - 3) | (4; -12) | (8; 10) | |
| (-5; 7) | (7; -2) | (11; 20) | |
| (-12; -1) | (0; -10) | (4; 12) | |
| (-10; 9) | (2; 0) | (6; 22) | |
| (0; 2) | (12; -7) | (16; 15) | |
| (-9; 6) | (3; -3) | (7; 19) | |
| (1; 0) | (13; -9) | (17; 13) | |
| (-4; 10) | (8; 1) | (12; 23) | |
| (2; 5) | (14; -4) | (18; 18) | |
| (-1; 4) | (11; -5) | (15; 17) |
Задание 5. Найти  (см. табл. 5) при различных заданных в таблице значениях а.
(см. табл. 5) при различных заданных в таблице значениях а.
Т а б л и ц а 5
| Номер задачи | y | a |

| 2; 3; ∞ | |

| 0; 2; ∞ | |

| 3; -3; ∞ | |

| -3; -2; ∞ | |

| 2; 4; ∞ | |

| 2; 5; ∞ | |

| 1; -4; ∞ | |

| 5; -5; ∞ | |

| -2; 1; ∞ | |

| -2; -1; ∞ |
Задание 6. Исследовать функцию y = f(x) (см. табл. 6) и построить ее график.
Т а б л и ц а 6
| Номер задачи | f(x) |

| |

| |

| |
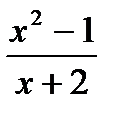
| |
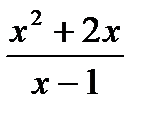
| |

| |

| |

| |

| |

|
Задание 7. Вычислить следующие интегралы (см. табл. 7). Для неопределенных интегралов результаты проверить дифференцированием.
Т а б л и ц а 7
| Номер задачи | А | Б | В |

| 
| 
| |

| 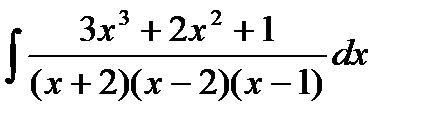
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 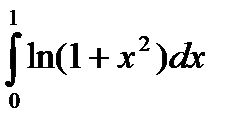
| |

| 
| 
|
Задание 8. Найти общее решение дифференциального уравнения и его частное решение (решение задачи Коши), удовлетворяющее начальному условию y ( x 0) = y 0(см. табл. 8).
Т а б л и ц а 8
| Номер задачи | Уравнение | x 0 | y 0 |

| 0,5p | ||

| |||

| |||

| -1 | 1,5 | |

| |||

| |||

| |||

| 1,2 | ||

| |||

| p | p |
Задание 9. В следующих задачах (см. табл. 9) вычислить площадь фигуры, ограниченной линиями y=f 1(x) и y=f 2(x). Сделать чертеж.
Т а б л и ц а 9
| Номер задачи | y =f 1(x) | y = f 2(x) |
| y = 4 – x 2 | y = x 2 – 2 x | |
| y = 2 x – x 2 + 3 | y = x 2 – 4 x + 3 | |
| y = 0,25 x 2 | y = 3 x – 0,25 x 2 | |
| y = x 2 – 2 x + 2 | y = 6 x – x 2 + 12 | |
| xy = 2 | x + 2 y = 5 | |
| xy = 8 | x + y – 9 = 0 | |
| y 2 = x + 4 | y = x – 2 | |
| xy = 5 | x + y = 6 | |
| xy = -2 | y = x – 3 | |
| y = (x + 1)2 | y 2 = x + 1 |
Задание 10. В следующих задачах (см. табл. 10) найти вероятность события методами комбинаторики.
Т а б л и ц а 10
| Номер задачи | Условие задачи |
| Из урны, содержащей 3 красных, 4 синих и 2 зеленых шара, берут наугад 2 шара. Какова вероятность того, что взятые шары окажутся одного цвета? | |
| Из колоды в 32 карты наугад берут три карты. Найти вероятность того, что не менее двух карт будут иметь одинаковую масть | |
| Брошены 3 игральные кости. Найти вероятность того, что 2 очка не выпадут ни на одной кости | |
| В урне лежат 8 занумерованных шаров. Наугад берут 4 шара. Найти вероятность того, что среди взятых шаров 3 будут иметь четные номера | |
| Из колоды в 52 карты наугад берут 4 карты. Какова вероятность того, что среди взятых карт окажется не менее двух тузов? | |
| В лотерее разыгрывается 30 билетов, среди которых 3 выигрышных. Какова вероятность получить более одного выигрышного билета, взяв наудачу 4 билета? | |
| Имеются 4 ящика, в которые наугад бросают шарики. Всего шариков 4. Какова вероятность того, что все шарики окажутся в одном ящике? | |
| 6 студентов условились ехать в одном электропоезде, но не договорились о вагоне. Какова вероятность того, что все поедут в одном вагоне, если в поезде 10 вагонов? | |
| Из партии в 100 деталей, содержащих 5% брака, берут для проверки 5 деталей. Партия принимается, если среди проверяемых деталей окажется не более одной бракованной. Найти вероятность приема партии | |
| Из ящика, в котором лежат 3 красных, 5 зеленых и 5 синих шаров, наугад берут 3 шара. Какова вероятность того, что взятые шары не будут одного цвета? |
Задание 11. Найти вероятность заданного события (см. табл. 11).
Т а б л и ц а 11
| Номер задачи | Условие задачи |
| Пассажир может обратиться за получением билета в одну из трех касс. Вероятности обращения в каждую кассу зависят | |
| от их местоположения и равны соответственно 0,7, 0,5 и 0,3. Вероятность того, что к моменту прихода пассажира имеющиеся в кассе билеты будут распроданы, равны: для первой кассы – 0,6, для второй – 0,2 и для третьей – 0,2. Пассажир подошел к одной из касс и приобрел билет. Найти вероятность того, что это была первая касса | |
| Имеется три ящика с подарочными наборами двух типов. В первом из них 15 наборов первого типа и 5 наборов второго типа, во втором – по десять наборов каждого типа, а в третьем – все 20 наборов – первого типа. Из наугад выбранного ящика извлекается один набор. Он оказался первого типа. Какова вероятность того, что этот набор извлечен из третьего ящика? | |
| В коробке находится 6 новых и 4 старых (игранных) теннисных мяча. Из ящика наугад вынимают два мяча, которыми играют, после чего их возвращают обратно в коробку. Через некоторое время из коробки вновь наугад берут для игры два мяча. Какова вероятность того, что оба мяча окажутся новыми (неигранными)? | |
| В экзаменационной программе 40 вопросов. Из них составлены билеты, в каждом из которых – два вопроса. Студент знает ответы на 30 вопросов. Найти вероятность того, что он сдаст экзамен, если для этого достаточно ответить на оба вопроса своего билета или на один вопрос билета и на один дополнительный вопрос из экзаменационной программы по выбору преподавателя | |
| На сборочном конвейере проходят сборку три изделия. К очередному перерыву в работе конвейера каждое из этих изделий может быть снято с конвейера с одинаковой вероятностью 0,4, и с вероятностью 0,5 на конвейер может поступить на сборку новое изделие. Найти вероятность того, что после перерыва на конвейере по-прежнему будет три изделия | |
| Прибор состоит из двух элементов, исправность каждого из которых необходима для работы прибора в целом. Вероятность выхода из строя первого элемента равна 0,8, а второго – 0,9. При включении прибора он вышел из строя. Найти вероятность того, что при этом вышел из строя только первый элемент | |
| У рыбака есть три излюбленных места для ловли рыбы, которые он посещает с одинаковой вероятностью. Если он закидывает удочку на первом месте, вероятность поймать рыбу равна 0,6, на втором – 0,4, а на третьем – 0,7. Известно, что, придя на рыбалку, он трижды забрасывал удочку и поймал только одну рыбу. Найти вероятность того, что он удил рыбу на первом месте | |
| В магазин “Фрукты” груши поставляют три агрофирмы в соотношении 5:8:7. Среди продукции первой фирмы стандарт составляет 90%, второй – 85%, а третьей – 75%. Найти вероятность того, что стандартная груша, приобретенная покупателем, поступила от третьей фирмы | |
| Три стрелка одновременно выстрелили по мишени. При этом две пули попали в мишень. Найти вероятность того, что третий стрелок попал в мишень, если известно, что вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,6, 0,5 и 0,4 | |
| Страховая компания разделяет застрахованных на три группы: малого, среднего и большого риска. Среди ее клиентов 50% принадлежат к группе малого риска, 30% – к группе среднего риска и 20% – к группе большого риска. Возникновение страхового случая (необходимости выплатить страховое возмещение) наступает для группы малого риска с вероятностью 0,01, для группы среднего риска – с вероятностью 0,03 и для группы большого риска – с вероятностью 0,08. Какова вероятность того, что застрахованный, получивший страховое возмещение, относится к группе малого риска? |