1. Пусть  — решение дифференциального уравнения
— решение дифференциального уравнения  . Показать, что введение новой искомой функции
. Показать, что введение новой искомой функции  приводит к дифференциальному уравнению, допускающему понижение порядка.
приводит к дифференциальному уравнению, допускающему понижение порядка.
2. Написать уравнение линии, на которой могут находиться точки перегиба графиков решений уравнения  .
.
3. Написать уравнение линии, на которой могут находиться точки графиков решений уравнения  , соответствующие максимумам и минимумам. Как отличить максимум от минимума?
, соответствующие максимумам и минимумам. Как отличить максимум от минимума?
4. Линейное дифференциальное уравнение останется линейным при замене независимой переменной  , где функция
, где функция  произвольная, но дифференцируемая достаточное число раз: Доказать это утверждение для линейного дифференциального уравнения второго порядка.
произвольная, но дифференцируемая достаточное число раз: Доказать это утверждение для линейного дифференциального уравнения второго порядка.
5. Доказать, что линейное дифференциальное уравнение остается линейный при преобразовании искомой функции
 .
.
Здесь 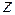 — новая искомая функция,
— новая искомая функция,  и
и  — произвольные, но достаточное число раз дифференцируемые функции.
— произвольные, но достаточное число раз дифференцируемые функции.
6. Составить общее.решение уравнения  , если известно ненулевое частное решение
, если известно ненулевое частное решение  этого уравнения.
этого уравнения.
7. Показать, что произвольные дважды дифференцируемые функции  и
и  являются решениями линейного дифференциального уравнения.
являются решениями линейного дифференциального уравнения.

8. Составить однородное линейное дифференциальное уравнение второго порядка, имеющее решения  ,
,  .
.
Показать, что функции  и
и 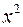 линейно -независимы в интервале
линейно -независимы в интервале  .
.
Убедиться в том, что определитель Вронского для этих функций равен нулю в точке 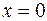 . Почему это не противоречит необходимому условию линейной независимости системы решений линейного однородного дифференциального уравнения?
. Почему это не противоречит необходимому условию линейной независимости системы решений линейного однородного дифференциального уравнения?
9. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка, если известны три линейно-независимые частные его решения  ,
,  и
и 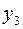 .
.
10. Доказать, что для того чтобы любое решение линейного однородного дифференциального уравнения с постоянными коэффициентами удовлетворяло условию  , необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные действительные части.
, необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные действительные части.
Расчетные задания
Задача 1. Найти общий интеграл дифференциального уравнения. (Ответ представить в виде  .)
.)
1.1.  1.2.
1.2. 
1.3.  1.4.
1.4. 
1.5.  1.6.
1.6. 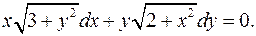
1.7. 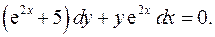 1.8.
1.8. 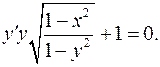
1.9.  1.10.
1.10. 
1.11.  1.12.
1.12. 
1.13.  1.14.
1.14. 
1.15.  1.16.
1.16. 
1.17.  1.18.
1.18. 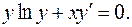
1.19. 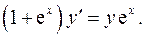 1.20.
1.20. 
1.21. 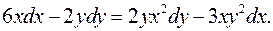 1.22.
1.22. 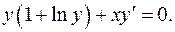
1.23.  1.24.
1.24. 
1.25.  1.26.
1.26. 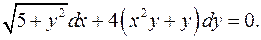
1.27. 
 1.28.
1.28. 
1.29.  1.30.
1.30. 
1.31. 
Задача 2. Найти общий интеграл дифференциального уравнения.
2.1.  2.2.
2.2. 
2.3.  2.4.
2.4. 
2.5.  2.6.
2.6. 
2.7.  2.8.
2.8. 
2.9.  2.10.
2.10. 
2.11.  2.12.
2.12. 
2.13.  2.14.
2.14. 
2.15.  2.16.
2.16. 
2.17.  2.18.
2.18. 
2.19. 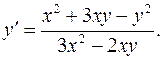 2.20.
2.20. 
2.21.  2.22.
2.22. 
2.23.  2.24.
2.24. 
2.25.  2.26.
2.26. 
2.27. 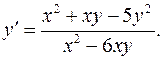 2.28.
2.28. 
2.29.  2.30.
2.30. 
2.31. 
Задача 3. Найти общий интеграл дифференциального уравнения.
3.1. 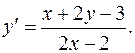 3.2.
3.2. 
3.3.  3.4.
3.4. 
3.5.  3.6.
3.6. 
3.7.  3.8.
3.8. 
3.9.  3.10.
3.10. 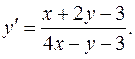
3.11.  3.12.
3.12. 
3.13.  3.14.
3.14. 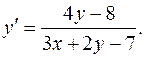
3.15.  3.16.
3.16. 
3.17. 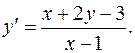 3.18.
3.18. 
3.19.  3.20.
3.20. 
3.21.  3.22.
3.22. 
3.23.  3.24.
3.24. 
3.25.  3.26.
3.26. 
3.27.  3.28.
3.28. 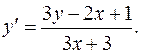
3.29.  3.30.
3.30. 
3.31. 
Задача 4. Найти решение задачи Коши.
4.1.  4.2.
4.2. 
4.3.  4.4.
4.4. 
4.5.  4.6.
4.6. 
4.7.  4.8.
4.8. 
4.9.  4.10.
4.10. 
4.11.  4.12.
4.12. 
4.13.  4.14.
4.14. 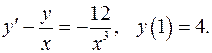
4.15.  4.16.
4.16. 
4.17.  4.18.
4.18. 
4.19.  4.20.
4.20. 
4.21.  4.22.
4.22. 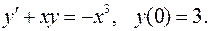
4.23.  4.24.
4.24. 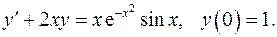
4.25.  4.26.
4.26. 
4.27.  4.28.
4.28. 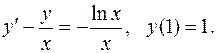
4.29.  4.30.
4.30. 
4.31. 
Задача 5. Решить задачу Коши.
5.1. 
5.2. 
5.3. 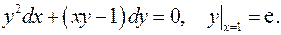
5.4. 
5.5. 
5.6. 
5.7. 
5.8. 
5.9. 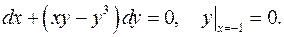
5.10. 
5.11. 
5.12. 
5.13. 
5.14. 
5.15. 
5.16. 
5.17. 
5.18. 
5.19. 
5.20. 
5.21. 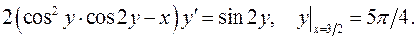
5.22. 
5.23. 
5.24. 
5.25. 
5.26. 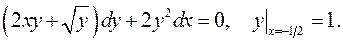
5.27. 
5.28. 
5.29. 
5.30. 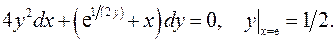
5.31. 
Задача 6. Найти решение задачи Коши.
6.1. 
6.2. 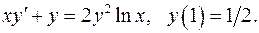
6.3. 
6.4. 
6.5. 
6.6. 
6.7. 
6.8. 
6.9. 
6.10. 
6.11. 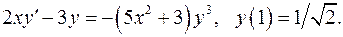
6.12. 
6.13. 
6.14. 
6.15. 
6.16. 
6.17. 
6.18. 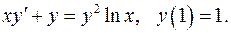
6.19. 
6.20. 
6.21. 
6.22. 
6.23. 
6.24. 
6.25. 
6.26. 
6.27. 
6.28. 
6.29. 
6.30. 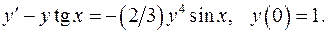
6.31. 
Задача 7. Найти общий интеграл дифференциального уравнения.
7.1. 
7.2. 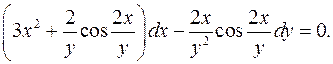
7.3. 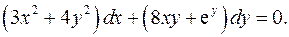
7.4. 
7.5. 
7.6. 
7.7. 
7.8. 
7.9. 
7.10. 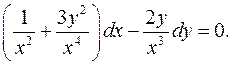
7.11. 
7.12. 
7.13.  7.14.
7.14. 
7.15.  7.16.
7.16. 
7.17. 
7.18.  7.19.
7.19. 
7.20. 
7.21. 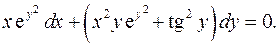
7.22. 
7.23. 
7.24. 
7.25. 
7.26. 
7.27. 
7.28. 
7.29. 
7.30. 
7.31. 
Задача 8. Для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через точку 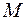 .
.
8.1.  8.2.
8.2. 
8.3.  8.4.
8.4. 
8.5. 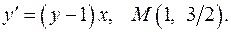 8.6.
8.6. 
8.7. 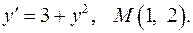 8.8.
8.8. 
8.9.  8.10.
8.10. 
8.11.  8.12.
8.12. 
8.13.  8.14.
8.14. 
8.15.  8.16.
8.16. 
8.17.  8.18.
8.18. 
8.19. 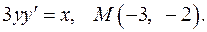 8.20.
8.20. 
8.21.  8.22.
8.22. 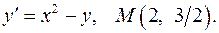
8.23. 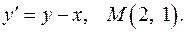 8.24.
8.24. 
8.25.  8.26.
8.26. 
8.27.  8.28.
8.28. 
8.29.  8.30.
8.30. 
8.31. 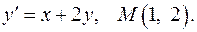
Задача 9. Найти линию, проходящую через точку 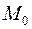 и обладающую тем свойством, что в любой ее точке
и обладающую тем свойством, что в любой ее точке 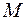 нормальный вектор
нормальный вектор  с концом на оси
с концом на оси  имеет длину, равную
имеет длину, равную 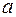 , и образует острый угол с положительным направлением оси
, и образует острый угол с положительным направлением оси  .
.
9.1.  9.2.
9.2. 
9.3.  9.4.
9.4. 
9.5. 
Найти линию, проходящую через точку 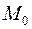 , если отрезок любой ее касательной между точкой касания и осью
, если отрезок любой ее касательной между точкой касания и осью  делится в точке пересечения с осью абсцисс в отношении
делится в точке пересечения с осью абсцисс в отношении  (считая от оси
(считая от оси  ).
).
9.6.  9.7.
9.7. 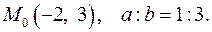
9.8.  9.9.
9.9. 
9.10. 
Найти линию, проходящую через точку 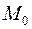 , если отрезок любой ее касательной между точкой касания и осью
, если отрезок любой ее касательной между точкой касания и осью  делится в точке пересечения с осью абсцисс в отношении
делится в точке пересечения с осью абсцисс в отношении  (считая от оси
(считая от оси  ).
).
9.11. 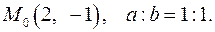 9.12.
9.12. 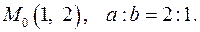
9.13.  9.14.
9.14. 
9.15. 
Найти линию, проходящую через точку 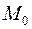 , если отрезок любой ее касательной, заключенный между осями координат, делится в точке касания в отношении
, если отрезок любой ее касательной, заключенный между осями координат, делится в точке касания в отношении  (считая от оси
(считая от оси  ).
).
9.16.  9.17.
9.17. 
9.18.  9.19.
9.19. 
9.20. 
Найти линию, проходящую через точку 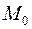 и обладающую тем свойством, что в любой ее точке
и обладающую тем свойством, что в любой ее точке 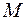 касательный вектор
касательный вектор  с концом на оси
с концом на оси 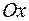 имеет проекцию на ось
имеет проекцию на ось 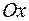 , обратно пропорциональную абсциссе точки
, обратно пропорциональную абсциссе точки 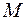 . Коэффициент пропорциональности равен
. Коэффициент пропорциональности равен 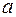 .
.
9.21.  9.22.
9.22. 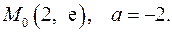
9.23.  9.24.
9.24. 
9.25. 
Найти линию, проходящую через точку 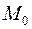 и обладающую тем свойством, что в любой ее точке
и обладающую тем свойством, что в любой ее точке 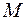 касательный вектор
касательный вектор  с концом на оси
с концом на оси  имеет проекцию на ось
имеет проекцию на ось  , равную
, равную 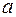 .
.
9.26.  9.27.
9.27. 
9.28.  9.29.
9.29. 
9.30.  9.31.
9.31. 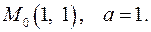
Задача 10. Найти общее решение дифференциального уравнения.
10.1. 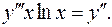 10.2.
10.2. 
10.3.  10.4.
10.4. 
10.5.  10.6.
10.6. 
10.7.  10.8.
10.8. 
10.9.  10.10.
10.10. 
10.11. 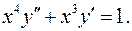 10.12.
10.12. 
10.13. 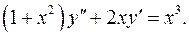 10.14.
10.14. 
10.15.  10.16.
10.16. 
10.17. 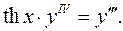 10.18.
10.18. 
10.19.  10.20.
10.20. 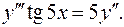
10.21.  10.22.
10.22. 
10.23.  10.24.
10.24. 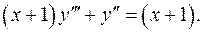
10.25.  10.26.
10.26. 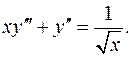
10.27.  10.28.
10.28. 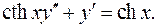
10.29.  10.30.
10.30. 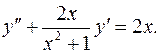
10.31. 
Задача 11. Найти решение задачи Коши.
11.1. 
11.2. 
11.3. 
11.4. 
11.5. 
11.6. 
11.7. 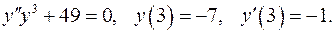
11.8. 
11.9. 
11.10. 
11.11. 
11.12. 
11.13. 
11.14. 
11.15. 
11.16. 
11.17. 
11.18. 
11.19. 
11.20. 
11.21. 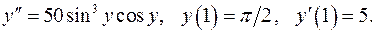
11.22. 
11.23. 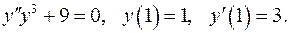
11.24. 
11.25. 
11.26. 
11.27. 
11.28. 
11.29. 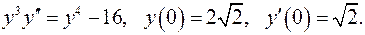
11.30. 
11.31. 
Задача 12. Найти общее решение дифференциального уравнения.
12.1.  12.2.
12.2. 
12.3.  12.4.
12.4. 
12.5.  12.6.
12.6. 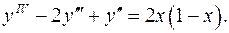
12.7. 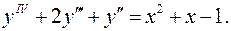 12.8.
12.8. 
12.9.  12.10.
12.10. 
12.11. 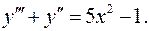 12.12.
12.12. 
12.13.  12.14.
12.14. 
12.15.  12.16.
12.16. 
12.17. 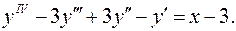 12.18.
12.18. 
12.19. 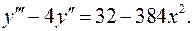 12.20.
12.20. 
12.21.  12.22.
12.22. 
12.23.  12.24.
12.24. 
12.25.  12.26.
12.26. 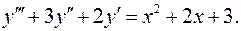
12.27.  12.28.
12.28. 
12.29. 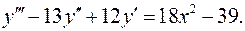 12.30.
12.30. 
12.31. 
Задача 13. Найти общее решение дифференциального уравнения.
13.1. 
13.2. 
13.3. 
13.4. 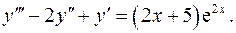
13.5. 
13.6. 
13.7. 
13.8. 
13.9. 
13.10. 
13.11. 
13.12. 
13.13. 
13.14. 
13.15. 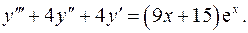
13.16. 
13.17. 
13.18. 
13.19. 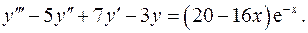
13.20. 
13.21. 
13.22. 
13.23. 
13.24. 
13.25. 
13.26. 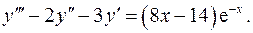
13.27. 
13.28. 
13.29. 
13.30. 
13.31. 
Задача 14. Найти общее решение дифференциального уравнения.
14.1. 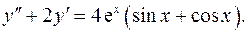 14.2.
14.2. 
14.3.  14.4.
14.4. 
14.5. 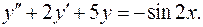 14.6.
14.6. 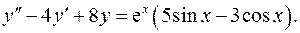
14.7.  14.8.
14.8. 
14.9.  14.10.
14.10. 
14.11.  14.12.
14.12. 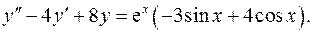
14.13.  14.14.
14.14. 
14.15.  14.16.
14.16. 
14.17.  14.18.
14.18. 
14.19.  14.20.
14.20. 
14.21.  14.22.
14.22. 
14.23.  14.24.
14.24. 
14.25.  14.26.
14.26. 
14.27.  14.28.
14.28. 
14.29.  14.30.
14.30. 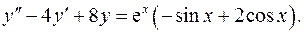
14.31. 
Задача 15. Найти общее решение дифференциального уравнения.
15.1. 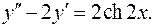
15.2. 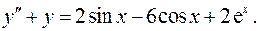
15.3. 
15.4. 
15.5. 
15.6. 
15.7. 
15.8. 
15.9. 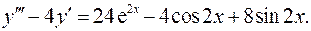
15.10. 
15.11. 
15.12. 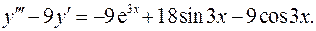
15.13. 
15.14. 
15.15. 
15.16. 
15.17. 
15.18. 
15.19. 
15.20. 
15.21. 
15.22. 
15.23. 
15.24. 
15.25. 
15.26. 
15.27. 
15.28. 
15.29. 
15.30. 
15.31. 
Задача 16. Найти решение задачи Коши.
16.1. 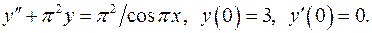
16.2. 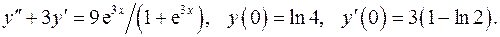
16.3. 
16.4. 
16.5. 
16.6. 
16.7. 
16.8. 
16.9. 
16.10. 
16.11. 
16.12. 
16.13. 
16.14. 
16.15. 
16.16. 
16.17. 
16.18. 
16.19. 
16.20. 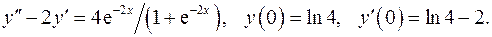
16.21. 
16.22. 
16.23. 
16.24. 
16.25. 
16.26. 
16.27. 
16.28. 
16.29. 
16.30. 
16.31. 
VI. РЯДЫ
Теоретические вопросы
1. Сходимость и сумма ряда. Необходимое условие сходимости ряда.
2. Теоремы сравнения.
3. Признаки Даламбера и Коши.
4. Интегральный признак сходимости ряда.
5. Теорема Лейбница. Оценка остатка знакочередующегося ряда.
6. Теорема о сходимости абсолютно сходящегося ряда. Свойства абсолютно сходящегося ряда.
7. Понятие равномерной сходимости.
8. Теорема о непрерывности суммы функционального ряда.
9. Теоремы о почленном интегрировании и почленном дифференцировании функционального ряда.
10. Теорема Абеля. Интервал и радиус сходимости степенного ряда.
11. Теорема о равномерной сходимости степенного ряда. Непрерывность суммы ряда.
12. Почленное интегрирование и дифференцирование степенных рядов.
13. Разложение функции в степенной ряд. Ряд Тейлора.
14. Разложение по степеням  бинома
бинома 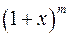 .
.
15. Условие разложимости функции в ряд Тейлора.
16. Разложение по степеням  функций
функций  ,
,  ,
,  ,
,  .
.