КРАТКИЙ КУРС ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ
«Элементы высшей математики»
Комбинаторика
Вопросы для изучения:
1. Правила суммы и произведения.
2. Факториал.
3. Размещения.
4. Перестановки.
5. Сочетания.
Правила суммы и произведения
При практической работе c реальным множеством, состоящим из набора элементов, которые могут быть как уникальными, так и повторяющимися, постоянно требуется отбирать отдельные элементы или группы элементов, организованные по какому-то критерию.
Рассмотрим пример: из 10 студентов надо выбрать трех для назначения в дежурство. Сколькими способами это можно сделать?
Поскольку выбор произволен, то первым дежурным можно назначить любого, т.е. число способов выбора, очевидно, 
вариантов. Но после того как выбран первый дежурный, второй выбирается уже из оставшихся 9 человек. Следовательно, число способов выбора второго дежурного 
вариантов. Ясно, что третий дежурный выбирается 
способами.
Таким образом, при произвольном последовательном выборе общее число способов выбора равно:
Указанный пример иллюстрирует следующее:
Правило произведения. Если объект 
можно выбрать из данного множества 
способами, объект 
– 
способами и так до k -го выбора, то все k выборов вместе могут быть выполнены 
способами.
Усложним пример. Пусть из контингента в 6 лейтенантов и 10 солдат надо выбрать усиленный патруль из 6 человек: трех офицеров и трех солдат.
Из предыдущего примера уже известно, что трех солдат можно выбрать m = 720 способами. Точно так же трех офицеров из шести выбираем 
способами. Ясно, что выборы солдат и офицеров не могут быть выполнены одновременно (сразу из множества в 16 человек), т.е. правило умножения для обобщения применить нельзя. Следовательно, общее число способов выбора равно 
.
Этот пример иллюстрирует следующее:
Правило суммы. Если два действия взаимно исключают друг друга, причем одно из них можно выполнить m способами, а другое – n способами, то выбрать либо первое, либо второе действие можно m + n способами.
Правило сложения легко обобщается на любое конечное число действий.
Представленные здесь правила умножения и суммы широко используются в комбинаторных и вероятностных задачах.
Факториал
Понятие факториала введем для множества 
неотрицательных чисел.
Факториалом целого положительного числа n называют произведение 
. Обозначение: n!. Чтение: «n факториал». Пример: 
Свойства факториала:
· Принимается: 
и 
.
· Факториал можно расчленить. К примеру,
· 
; 
; 
; 
.
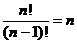Размещения
Пусть имеется некоторое множество, содержащее конечное число членов. Например, множество учебных групп факультета, множество книг на полке, множество населенных пунктов области или, например, множество целых положительных чисел, меньших 10, и т.д. Все элементы такого множества можно пронумеровать, т.е. каждому элементу множества поставить в соответствие одно из чисел: 1, 2, 3, 4, …, n; в результате получается некоторая последовательность элементов данного множества, которые обычно записывают в виде 
.Такие «занумерованные» множества будем называть упорядоченными. Таким образом, упорядоченное множество представим в виде некоторой последовательности, что будет использовано в дальнейшем. Очевидно, если в упорядоченном множестве поменять местами хотя бы два его элемента, то получим новое упорядоченное множество, которому будет соответствовать новая последовательность элементов данного множества.
Определение. Размещением из n элементов по m называется любое упорядоченное подмножество из m элементов множества, состоящего из n различных элементов.
Пример. Пусть имеется множество, содержащее четыре буквы: 
. Запишем все возможные размещения из четырех указанных букв по две. Таких размещений 12:
AB, AC, AD, BC, BD, CD, BA, CA, DA, CB, DB, DC.
Заметим, что размещения отличаются порядком входящих в них элементов и их составом. Размещения AB и BA содержат одинаковые буквы, но порядок их расположения различен. Поэтому эти размещения считаются разными.
На практике чаще представляет интерес количество размещений, а не их конкретный вид. Число размещений из n элементов по m будем обозначать символом 
, где 
.
Формула для определения числа размещений из n элементов по m имеет вид:
.
Достаточно часто удобно использовать иную формулу:
Таким образом, для приведенного выше примера:
Рассмотрим теперь размещения с повторениями.
Пусть имеется два числа {4; 5}. Из них можно составить 8 трехзначных чисел: 444, 544, 454, 445, 554, 545, 455, 555, что и иллюстрирует размещение из двух элементов по три с повторениями.
Определение. Размещения из n элементов, в каждое из которых входит m элементов, причем один элемент может повторяться в каждом размещении любое количество раз, но не более m раз, называются размещениями из n элементов по m с повторениями.
Формула для расчета:
Так, для примера, 
.
Перестановки
Рассмотрим теперь отдельно случай, когда m = n. Соответствующие этому случаю размещения называются перестановками.
Определение. Перестановкой из n элементов называется любое упорядоченное множество, в которое входят по одному разу все n различных элементов данного множества.
Пример. Пусть имеются цифры 3, 5, 7. Этому множеству цифр соответствует 6 перестановок: 357, 375, 537, 573, 753, 735.
Число перестановок n различных элементов будем обозначать символом 
.
Формула: число перестановок n различных элементов равно:
Так как перестановки являются частным случаем размещений, то при n = m имеем: 
Рассмотрим теперь случай с повторениями. Если каждый элемент множества {4; 5} взять по два раза, получим числа: 4455, 5544, 5454, 4545, 4554, 5445.
Определение. Перестановки из n объектов, в каждую из которых входят 
одинаковых объектов одного типа, 
– второго типа и т.д. до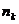 
– k- го типа, называются перестановками из n элементов с повторениями.
Число всех таких перестановок с повторениями:
.
Так, для примера, 
.
Сочетания
Если два различных размещения состоят из одинаковых элементов некоторого множества, то они обязательно отличаются порядком входящих в них элементов. Часто возникает необходимость не учитывать порядок элементов, входящих в размещение. В этом случае все m! размещения, которые состоят из одних и тех же m элементов, считаются неразличимыми.
Предположим, что из чисел 3, 5, 7 необходимо составить различные произведения двух чисел. Таких произведений только три, а именно: 3 ´ 5 = 15; 3 ´ 7 = 21; 5 ´ 7 = 35. Это объясняется тем, что произведения вида 3 ´ 5 и 5 ´ 3 совпадают, так как порядок сомножителей, входящих в произведение, не учитывается. Если требуется из указанных цифр составить двузначные числа, то таких чисел уже шесть. Запишем эти числа: 35, 53, 37, 73, 57, 75. Как видно, здесь уже пришлось учитывать порядок цифр, т.е. получим размещения.
Определение. Сочетанием из n элементов по m называется любое подмножество из m элементов, которые принадлежат множеству, состоящему из n различных элементов.
Пример. Пусть имеется множество, содержащее четыре буквы: { A, B, C, D }. Запишем все возможные сочетания из указанных букв по три. Таких сочетаний будет четыре: ABC, ACD, ABD, BCD. Здесь в число сочетаний не включены, например, ACB и BCA, так как эти последовательности букв не отличаются от последовательности ABC, поскольку порядок элементов в сочетаниях не учитывается.
Число сочетаний из n разных элементов по m будем обозначать символом 
, где .
Прежде чем привести общую формулу для определения числа сочетаний, решим следующую задачу. Необходимо выбрать 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Из смысла задачи следует, что порядок выбора книг не играет роли. Здесь важен только их состав. Как известно из предыдущего, число размещений из 10 по 4 равно 
. Пусть теперь выбраны 4 книги из 10. Число возможных выборов, где не учитывается порядок выбранных книг, равно 
. Однако каждому из этих сочетаний (выборов) будут соответствовать 
= 24 перестановки выбранных книг. Тогда выбор 4 книг из 10 с учетом их порядка по правилу умножения возможен 
способами. С другой стороны, число указанных способов – это число размещений 
. Таким образом, 
, откуда имеем 
. То есть число возможных способов выбора равно 210. Следовательно, число сочетаний из n элементов по m равно:
.
Следствие. Число сочетаний из n элементов по n – m равно числу сочетаний из n элементов по m, т.е.
.
Еще раз подчеркнем разницу между размещениями и сочетаниями: в размещениях учитывается порядок входящих в них элементов, а в сочетаниях – не учитывается. При решении задач это не следует забывать. Кроме того, следует иметь в виду, что использование правила умножения приводит к необходимости учитывать порядок элементов при выборе их из какого-либо множества.
Приведем два свойства числа сочетаний, которые могут быть полезными при решении комбинаторных задач.
· Имеет место равенство (правило Паскаля):
· Имеет место равенство:
.
Рассмотрим теперь задачу с повторениями.
Определение. Сочетаниями из n объектов называются соединения, содержащие m объектов (без учета порядка следования), причем любой объект может входить в соединение любое число раз, но не более m раз.
Таким образом, если имеется по m одинаковых предметов каждого из n различных типов, то число способов, которыми можно выбрать m из этих 
предметов определится формулой:
Пример. Сколькими способами можно выбрать четыре монеты из четырех пятирублевых и четырех рублевых монет?
Это – задача о числе сочетаний из двух по четыре с повторениями. Следовательно,
,
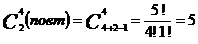то есть число таких выборов – пять.
Примеры решения задач