Лекция 2.
МАТРИЦЫ.
Основные понятия.
Матрицей размера m 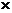 n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
Матрица обозначается заглавными буквами латинского алфавита, например: A, B, C,…, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: aij, где i – номер строки, j – номер столбца.
Пример: a).  ,
,
или, в сокращенной записи, A=(aij); i=1,2,…,m; j=1,2,…,n
b). B= 
в). C= 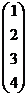 - матрица-столбец (вектор-столбец)
- матрица-столбец (вектор-столбец)
г). D=(1 2 3)= 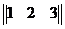 - матрица-строка (вектор-строка)
- матрица-строка (вектор-строка)
д). H=  =
=  =
= 
Если колличество строк матрицы равно колличеству столбцов, то матрица называется квадратной.
Элементы матрицы aij, у которых номер столбца равен номеру строки (i=j), называются диагональными и образуют главную диагональ матрицы.
Пример: Для квадратной матрицы главную диагональ образуют
элементы a11, a22, …, ann.
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.
Пример: A=  - диагональная матрица третьего порядка.
- диагональная матрица третьего порядка.
Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-го порядка, она обозначается буквой E.
Пример: Е=  - единичная матрица третьего порядка.
- единичная матрица третьего порядка.
Матрица любого размера называется нулевой, или нуль-матрицей, если все её элементы равны нулю.
Пример: 
Операции над матрицами.
1. Умножение матрицы на число. Произведением матрицы А на число l называется матрица В=lА, элементы которой bij=lаij для i=1,2,…,m; j=1,2,…,n.
Пример: Если А=  , то 5А=
, то 5А= 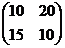 .
.
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Пример:  .
.
2. Сложение матриц. Матрицы одного типа можно складывать по следующему принципу:
А=  , В=
, В= 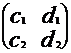 , А+В=
, А+В=  ,
,
т.е. матрицы складываются поэлементно.
Пример: А= 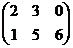 , В=
, В=  , С=А+В=
, С=А+В= 
3. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц 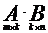 называется такая матрица
называется такая матрица  , каждый элемент которой сij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.
, каждый элемент которой сij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.
Пример: Вычислить произведение матриц А×В, где А=  , В=
, В= 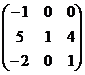 .
.
1. Найдем размер матрицы-произведения (если умножение матриц возможно): 
2. Вычислим элементы матрицы-произведения С, умножая элементы каждой строки матрицы А на соответствующие элементы столбцов матрицы В следующим образом: С= 
Получаем С= 
Примечание. В общем случае умножение матриц не обладает переместительным законом: А×В¹В×А
Пример: а).Найдем произведение В×А матриц из предыдущего примера
 , число столбцов матрицы В не равно числу строк матрицы А, Þ произведение матриц не существует.
, число столбцов матрицы В не равно числу строк матрицы А, Þ произведение матриц не существует.
б). А=  , В=
, В= 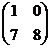
А×В=  ×
× 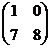 =
= 
В×А= 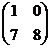 ×
×  =
= 
А×В¹ В×А
Но существует два исключения:
1. Умножение на единичную матрицу обладает переместительным законом: А×Е=Е×А=А, где Е= 
Пример: А=  , Е=
, Е=  ,
,
А×Е=  ×
×  =
= 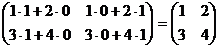 =А
=А
Е×А=  ×
×  =
=  =А
=А
2. Произведение взаимно-обратных матриц подчиняется переместительному закону: В×В-1=В-1×В=Е
4. Возведение в степень. целой положительной степенью Аm (m>0) квадратной матрицы А называется произведение m матриц, равных А, т.е. Аm= 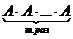 .
.
Примечание. Операция возведения в степень определена только для квадратных матриц.
Пример: А=  , А2=
, А2=  ×
×  =
=  .
.
5. Транспонирование матрицы – переход от матрицы А к матрице А’, в которой строки и столбцы поменялись местами.
Пример: А= 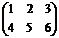 , А’=
, А’=  .
.
Обратная матрица.
Для каждого числа а¹0 существует обратное число а-1 такое, что произведение а×а-1=1. Для квадратных матриц вводится аналогичное понятие.
1. Матрица А-1 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как слева, так и справа получается единичная матрица:
А-1×А=А×А-1=Е
2. Найти матрицу обратную данной.
Пусть дана матрица В=  .
.
Соответствующий этой матрице определитель (детерминант) имеет вид:
D=det B=  .
.
Если det B=0, то обратная матрица не существует. И наоборот, если обратная матрица не существует, то det B=0.
Если det B¹0, то обратная матрица находится по формуле:
В-1= 
где Аij – алгебраические дополнения элементов аij матрицы В.
Пример: В= 
D=detB=  =0+11+6=17¹0
=0+11+6=17¹0
A11=  =-4, A21=
=-4, A21=  =-1, A31=
=-1, A31=  =4,
=4,
A12= 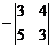 =11, A22=
=11, A22=  =-10,,A32=-
=-10,,A32=-  =6,
=6,
A13=  =3, A23=
=3, A23=  =5, A33=
=5, A33=  =-3.
=-3.
В-1=  =
= 
Это и есть матрица, обратная данной.
Ранг матрицы.
В матрице А размером m 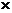 n вычеркиванием каких-либо строк и столбцов можно вычленить квадратные матрицы k -го порядка, где k £min(m,n). Определители таких подматриц называются минорами k-го порядка.
n вычеркиванием каких-либо строк и столбцов можно вычленить квадратные матрицы k -го порядка, где k £min(m,n). Определители таких подматриц называются минорами k-го порядка.
Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.
Ранг матрицы обозначается rang A или r(A).
Пример: Вычислить ранг матрицы А= 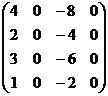 .
.
Матрица А имеет четвертый порядок, поэтому r (А)£4.
Однако 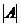 =0, т.к. матрица А содержит нулевой столбец, поэтому r (А)£3. Все подматрицы третьего порядка тоже содержат нулевой столбец поэтому имеют нулевые определители, значит r (А)£2. Все подматрицы второго порядка либо имеют нулевой столбец (второй и четвертый), либо имеют пропорциональные столбцы (первый и третий), поэтому тоже имеют нулевые определители; таким образом r (А)£1. Поскольку матрица А имеет ненулевые элементы, то r (А)=1.
=0, т.к. матрица А содержит нулевой столбец, поэтому r (А)£3. Все подматрицы третьего порядка тоже содержат нулевой столбец поэтому имеют нулевые определители, значит r (А)£2. Все подматрицы второго порядка либо имеют нулевой столбец (второй и четвертый), либо имеют пропорциональные столбцы (первый и третий), поэтому тоже имеют нулевые определители; таким образом r (А)£1. Поскольку матрица А имеет ненулевые элементы, то r (А)=1.
Решение систем линейных уравнений
Матричным способом.
Пример: Решить систему уравнений  .
.
В=  , С=
, С=  , X=
, X=  .
.
Тогда система в матричной форме имеет вид
В×X=C
Умножим обе части этого равенства с левой стороны на В-1
В-1×В×X= В-1×C
E×X= В-1×C
X= В-1×C –
решение в матричной форме.
Таким образом, для решения системы уравнений в матричной форме 1). Находим матрицу, обратную матрице системы.
2). Для получения ответа в обычной форме выполняем умножение матриц в правой части решения.
1). D= 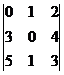 =0+6+20-0-0-9=17
=0+6+20-0-0-9=17
А11=  =-4, А21=-
=-4, А21=-  =-1, А31=
=-1, А31=  =4,
=4,
А12= 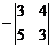 =11,А22=
=11,А22=  =-10, А32=
=-10, А32=  =6,
=6,
А13=  =3, А23=
=3, А23=  =5, А33=
=5, А33=  =-3
=-3
В-1= 
2). X= В-1×C=  ×
×  =
= 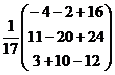 =
=  =
= 
Ответ: x=  , y=
, y=  , z=
, z=  .
.