ДМ. Лекция
Тема «Комбинаторика»
Комбинаторика – раздел дискретной математики, который посвящен решению задач пересчета и перечисления элементов множества (обычно конечного), обладающих заданным набором свойств.
Если требуется найти число элементов, принадлежащих данному множеству и обладающих заданными свойствами, то это задача пересчета. Если необходимо выделить все элементы множества, удовлетворяющие заданным свойствам, то это задача перечисления.
Решение многих комбинаторных задач основано на следующих двух правилах.
Правила суммы и произведения
Пусть Х – конечное множество такое, что | X | = n. Тогда говорят, что объект х из Х может быть выбран n способами. Пусть Х1, …, Хn – попарно непересекающиеся множества, то есть Хi ∩ Xj = Æ при любых i ≠ j. Тогда, очевидно, выполняется равенство 
.
В комбинаторике этот факт называется правилом суммы. Для n = 2 оно формулируется следующим образом: « Если объект x может быть выбран m способами, а объект y – другими n способами, то выбор “либо x, либо y ” может быть осуществлен m + n способами ».
Другим часто применяемым в комбинаторике правилом является правило произведения. Сформулируем и докажем частный случай этого правила для кортежа длины 2: « Если объект x может быть выбран m способами и после каждого из таких выборов объект y в свою очередь может быть выбран n способами, то выбор упорядоченной пары (x, y) может быть осуществлен m ∙ n способами ».
Доказательство
В общем случае правило произведенияформулируется следующим образом: « Если объект x1 может быть выбран n1 способами, после чего объект x2 может быть выбран n2 способами и для любого i, где 2 ≤ i ≤ m - 1, после выбора объектов x1,..., xi объект xi+1 может быть выбран ni+1 способами, то выбор кортежа (x1, x2,..., xm) длины m может быть осуществлен n1 ∙ n2 ∙ … ∙ nm способами ».
Правило произведения в общем случае доказывается методом математической индукции.
Размещения и сочетания
def. Набор элементов 
, …, 
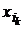из множества Х = { x1,.., xn } называется выборкой объема k из n элементов или (n, k) -выборкой.
def. Выборка называется упорядоченной, если в ней задан порядок следования элементов.
Таким образом, упорядоченная (n, k)-выборка представляет собой кортеж длины k, составленный из элементов множества мощности n. Следовательно, две различные упорядоченные (n, k)-выборки различаются лишь порядком расположения элементов в них.
def. Выборка называется неупорядоченной, если порядок следования элементов в ней не является существенным.
Две различные неупорядоченные (n, k)-выборки обязательно отличаются друг от друга хотя бы одним элементом.
В выборках могут допускаться или не допускаться повторения элементов.
def. Упорядоченная (n, k)-выборка, в которой элементы могут повторяться, называется (n, k) -размещением с повторениями.
def. Упорядоченная(n, k)-выборка, элементы которой попарно различны, называется (n, k) -размещением без повторений.
def. Перестановкой без повторений из n элементов (или перестановкой множества X мощности n) называется (n, n)-размещение без повторений.
def. Неупорядоченная (n, k)-выборка, в которой элементы могут повторяться, называется (n, k) -сочетанием с повторениями.
def. Неупорядоченная (n, k)-выборка, элементы которой попарно различны, называется (n, k) -сочетанием без повторений.
Заметим, что любое (n, k)-сочетание без повторений можно рассматривать как k -элементное подмножество n -элементного множества.
Пример 1. Пусть Х = { a, b, c }. Тогда
1. (a, a),(a, b),(a, c),(b, a),(b, b),(b, c),(c, a),(c, b),(c, c) – (3,2)-размещения с повторениями;
2. (a, b), (a, c), (b, a), (b, c), (c, a), (c, b) – (3,2)-размещения;
3. { a, a }, { a, b }, { a, c }, { b, b }, { b, c }, { c, c } – (3,2)-сочетания с повторениями;
4. { a, b }, { a, c }, { b, c } – (3,2)-сочетания.
Число (n, k)-размещений с повторениями обозначается через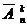 
, а без повторений – 
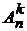. Число перестановок без повторений из n э лементов обозначается через Pn, то есть Pn = 
. Число (n, k)-сочетаний с повторениями обозначаем через 
, а без повторений – 
.
Утверждение 1. 
= 
.
Доказательство.
Соглашение. В дальнейшем для общности формул условимся считать, что 0! = 1.
Утверждение 2. 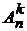= n ∙ (n - 1) ∙ … ∙ (n - k+1) = 
при k ≤ n и 
= 0 при k > n.
Доказательство.
Следствие. Pn = 
= n ∙ (n - 1) ∙ … ∙ 1 = n!.
Утверждение 3. 
= 
= 
при k ≤ n и = 0 при k > n.
Доказательство.
Утверждение 4. = 
.
Доказательство.
Пример 2. Пусть n = 4, k = 8, X = {1, 2, 3, 4}, B ={1, 1, 1, 2, 3, 3, 4, 4} –
(4, 8)-сочетание с повторениями. Тогда a(В) =. Обратно, если a(В) = (1, 0, 0, 1, 0, 0, 0, 1, 0), то однозначно получаем, что
В =.
Замечание 1. При определении выборки предполагалось, что она содержит, по крайней мере, один элемент. Однако для общности рассуждений в число выборок часто включают и пустую выборку, не содержащую элементов. Она единственна для всех рассмотренных нами случаев. Следовательно, 
= 
= 
= 
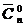= 1. При этом формулы, приведенные в утверждениях 1–4 остаются справедливыми.
Выше мы определили понятие перестановки без повторений из n элементов. Понятие перестановки с повторениями рассматривается в случае, когда имеется n элементов, которые можно разбить на k групп, так что элементы, входящие в одну группу, неразличимы между собой и отличны от элементов, входящих в другие группы. Пусть число элементов в каждой группе равно соответственно n1, n2,..., nk, то есть n1 + n2 + … + nk = n.
def. Пусть имеется n элементов, которые можно разбить на k групп так, что элементы, входящие в одну группу, неразличимы между собой и отличны от элементов, входящих в другие группы. Перестановкой с повторениямииз n элементов называется кортеж длины n, составленный из этих элементов.
Если число элементов в каждой группе равно соответственно n1, n2,..., nk, то есть n1 + n2 + … + nk = n, то число всех перестановок с повторениями из n элементов обозначается через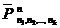 
.
Утверждение 5. =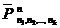 
.
Доказательство.
Схема определения вида комбинаторной конфигурации
 |
Примеры решения задач
Пример 3. Бросают две игральные кости (с шестью гранями каждая). Сколькими способами они могут упасть так, что либо на каждой грани выпадет четное число очков, либо на каждой грани выпадет нечетное число очков?
Решение.
Пример 4. Сколькими способами три награды (за первое, второе и третье места) могут быть распределены между 10 участниками соревнований?
Решение.
Пример 5. Имеется 10 различных книг. Сколькими способами их можно расставить на полке?
Решение.
Пример 6. Сколько двузначных чисел можно составить, используя цифры 7, 4 и 5?
Решение.
Пример 7. Сколькими способами можно вытянуть 5 карт трефовой масти из стандартной колоды, содержащей 52 карты?
Решение.
Пример 8. В магазине продается 4 сорта пирожных: бизе, эклеры, песочные, наполеоны. Сколькими способами можно выбрать 7 пирожных?
Решение.
Пример 9. У врача 3 таблетки одного лекарства, 2 таблетки – другого и 4 таблетки – третьего. Сколькими способами он может распределить прием имеющихся таблеток по одной в день?
Решение.
Бином Ньютона
Исторически название бином Ньютона несправедливо, поскольку формулу 
знали еще среднеазиатские математики, начиная с Хайяма (Омар Хайям (около 1048 – 1131) – персидский поэт, математик и философ), а в Европе до Ньютона (Исаак Ньютон (1643 – 1727) – английский физик, астроном и математик) еe знал Паскаль (Блез Паскаль (1623 – 1662) – французский математик). Однако заслуга Ньютона заключается в том, что он обобщил эту формулу для нецелого показателя n (см. замечание 2.2).
Для натурального показателя n формула бинома Ньютона имеет вид:
= 
= 
. (9)
Доказательство.
Замечание 2. Для нецелого n при | х | < 1, формула имеет вид
= 