Пусть имеется некоторая последовательность чисел 
. Рассмотрим степенной ряд.
.
Если этот ряд сходится в некоторой области к функции 
, то эту функцию называют производящей для последовательности чисел . Например, используя разложения
и уже знакомое нам
,
можно утверждать, что для последовательностей: 1,1,...,1,...; 1,2,3,...,n,..., и 
производящими функциями являются функции 1/(1-x), 1/(1-x)2 и (1+x)k соответственно.
В комбинаторике интересуются производящими функциями для последовательностей 
связанных с комбинаторными задачами. Так, с помощью производящей функции 
легко доказать, что
и многие другие соотношения, полезные в комбинаторике.
Рассматривая перестановки в некотором множестве с n элементами, была получена формула (2.2):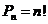 
, для которой использовались соотношения:
.
Соотношение, в котором текущее значение выражения вычисляется на основе предыдущих, называется рекуррентным или рекурсивным. Примером рекуррентного соотношения может служить формула генерирования чисел Фибоначчи 
(2.18)
где текущее значение вычислено на основе значения двух предыдущих. Числа Фибоначчи тесно связанны с комбинаторными коэффициентами. Так, число равно числу всех возможных различных n – последовательностей, состоящих из 0 и 1, в которых содержится не более k – единиц, причём ни одна пара единиц не располагается рядом. Из последнего требования следует, что 
. Таким образом, k может принимать значения от 0 до 
, где символ 
означает целую часть a.
Рассмотрим последовательность из n элементов, в которой k не стоящих рядом единиц, а оставшиеся элементы равны нулю. Тогда, чтобы единицы не стояли рядом, необходимо схему такой последователь
 |
ности изобразить, как на рис. 2.3., где в блоке b1 и bk+1 могут быть нули, а в блоках bj
должно быть не менее одного нуля в каждом, причем всего нулей должно быть (n - k).
Рис. 2.3. Схема вычисления чисел Фибоначчи
Очевидно, что, если в последовательности k единиц, то положение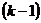 
нулей уже фиксировано необходимостью отделить единицы друг от друга. Оставшиеся 
нулей необходимо распределить по 
«корзинам» 
, 
. Чтобы найти число возможных комбинаций, воспользуемся результатами решения задачи 7 данного раздела. Получим:
Таким образом, для F(n) можем записать:
или в несколько ином виде:
(2.19)
Рекуррентные соотношения можно получить и с помощью производящих функций. Например, рассмотрим биномиальное разложение:
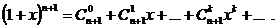(2.20)
Вместе с тем можно записать:
(2.21)
Сравнивая (2.20) и (2.21), получим рекурентное соотношение:
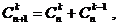(2.22)
где 
.
Задачи и упражнения
1. Сколько существует перестановок из n элементов, в которых между двумя данными элементами стоит r элементов?
2. Сколькими способами можно разместить n гостей за круглым столом?
3. Сколько различных слов можно составить, переставляя буквы слова «комбинаторика»?
4. Сколько можно сделать костей домино, используя числа 0,1,...,r?
5. Сколько целых положительных решений имеет уравнение x1+x2+...+xm=n?
6. Доказать, что для биномиальных коэффициентов справедливо равенство
7. Методом траекторий или другим способом доказать, что
8. Доказать, что 
если k<(n-1)/2 и 
если k>(n-1)/2.
9. Найти наибольшее среди чисел 
.
10. Доказать, что сумма всех полиномиальных коэффициентов в разложении (x1+x2+...+xk)n равно kn.
11. Используя биномиальное разложение, доказать тождества:
а) 
;
б) 
;
в) 
.
12. Используя свойства биномиального разложения, вычислить:
а) 
;
б) 
;
в) 
.
13. Определить количество прямоугольных матриц размерности 
с элементами из {0,1} с попарно различными строками (m<=2).
14. Из колоды, состоящей из 52 карт, выбрали 10 карт. Определить, в скольких случаях среди них окажутся:
а) пиковая дама; б) все четыре дамы; в) все карты одной масти;
г) ни одного туза; д) ровно один туз; е) хотя бы один туз;
ж) ровно два туза.
15. Найти количество целочисленных решений системы:
а) 
;
б) 
.
16. Вывести соотношение (2.19) для чисел Фибоначчи, используя идеи задачи 2.7 этого раздела.