Для построения соответствующих математических моделей комбинаторных задач будем использовать математический аппарат теории множеств. Может случиться, что в данном множестве порядок следования элементов не важен, а важен только состав множества. Но есть задачи, в которых прядок элементов является существенным.
Определение 1:Порядок во множестве  из
из  элементов – это нумерация его элементов натуральными числами, т.е. отображение множества
элементов – это нумерация его элементов натуральными числами, т.е. отображение множества  на множество
на множество  .
.
Определение 2: Множество с заданным на нем порядком называется упорядоченным множеством.
Очевидно, что множество, содержащее более одного элемента, можно упорядочить не единственным способом.
Например, из двух букв  и
и  можно построить упорядоченное множество двумя различными способами:
можно построить упорядоченное множество двумя различными способами:
 и
и 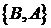 .
.
Три буквы  ,
,  и
и  можно расположить в виде последовательности шестью способами:
можно расположить в виде последовательности шестью способами:
 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Для четырех букв путем перебора получим уже 24 различных упорядоченных последовательностей.
Упорядоченные последовательности элементов некоторого множества можно рассматривать как распределения или расстановки этих элементов в последовательности.
Определение 3: Пусть дано конечное множество  из
из  элементов. Всякий набор из
элементов. Всякий набор из 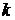 элементов данного множества (при этом элементы в наборе могут и повторяться) будем называть
элементов данного множества (при этом элементы в наборе могут и повторяться) будем называть 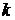 - расстановками.
- расстановками.
Через понятие расстановки вводятся основные определения комбинаторики: сочетания, размещения и перестановки. При этом каждое из этих понятий может быть с повторениями и без повторений. В данном параграфе будут рассмотрены комбинаторные формулы без повторений.
Перестановки без повторений.
Определение 4: Пусть  - конечное множество из
- конечное множество из  элементов. Перестановками из
элементов. Перестановками из  различных элементов множества
различных элементов множества  называются все расположения
называются все расположения  элементов в определенном порядке. Обозначается:
элементов в определенном порядке. Обозначается:  (от французского слова permutation - перестановка).
(от французского слова permutation - перестановка).
Упорядоченные множества считаются различными, если они отличаются либо своими элементами, либо их порядком.
Определение 5: Различные упорядоченные множества, которые отличаются лишь порядком элементов, называются перестановками этого множества.
Последнее определение сформулировано с позиции теории множеств.
Определение 6: Произведение  последовательных натуральных чисел в математике обозначают
последовательных натуральных чисел в математике обозначают 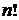 и называют факториалом.
и называют факториалом.
Выбор для обозначения 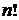 восклицательного знака, возможно, связан с тем, что даже для сравнительно небольших значений
восклицательного знака, возможно, связан с тем, что даже для сравнительно небольших значений  число
число 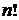 очень велико. Например,
очень велико. Например,  ,
,  ,
,  ,
,  ,
,  ,
, 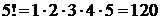 ,
, 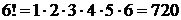 и т.д.
и т.д.
Теорема 1: Число перестановок из  различных элементов вычисляется по формуле:
различных элементов вычисляется по формуле:
 (1)
(1)
Доказательство. Рассмотрим произвольное множество из  элементов. Построим всевозможные расстановки из этих
элементов. Построим всевозможные расстановки из этих  элементов. На первое место расстановки можно поставить любой из
элементов. На первое место расстановки можно поставить любой из  элементов (
элементов ( способов выбора первого элемента). После того, как первый элемент выбран и независимо как он выбран, второй элемент можно выбрать
способов выбора первого элемента). После того, как первый элемент выбран и независимо как он выбран, второй элемент можно выбрать  способом. Для выбора третьего элемента остается
способом. Для выбора третьего элемента остается  способа и т.д. Последний элемент выбирается соответственно одним способом. Тогда, в силу комбинаторного принципа умножения, количество таких расстановок будет равно:
способа и т.д. Последний элемент выбирается соответственно одним способом. Тогда, в силу комбинаторного принципа умножения, количество таких расстановок будет равно:

Теорема доказана.
Пример 1: Сколькими способами трое друзей могут занять в кинотеатре места с номерами 1, 2 и 3.
Решение. Количество искомых способов будет равно числу перестановок без повторений из трех элементов:  способов. При необходимости эти способы можно перебрать.
способов. При необходимости эти способы можно перебрать.
Перестановки букв некоторого слова называют анаграммами. Открытые еще в ІІІ веке до нашей эры греческим грамматиком Ликофроном анаграммы до сих пор привлекают внимание языковедов, поэтов и любителей словесности. Мастера словесных игр помимо эрудиции и большого запаса слов знают много секретов, связанных с комбинаторными навыками, один из которых – анаграммы. Часто требуется среди всех перестановок выбрать те, которые обладают определенным свойством. Например, среди анаграмм слова «крот», которых всего  , только одна, не считая самого слова «крот», имеет смысл в русском языке – «корт».
, только одна, не считая самого слова «крот», имеет смысл в русском языке – «корт».
Кроме линейных перестановок, можно рассматривать перестановки круговые (или циклические). В этом случае перестановки, переходящие друг в друга при вращении, считаются одинаковыми и не должны засчитываться.
Теорема 2: Число круговых перестановок из  различных элементов равно
различных элементов равно 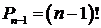
Пример 2: Сколькими способами 7 детей могут стать в хоровод?
Решение. Число линейных перестановок 7 детей будет равно  . Если хоровод уже сформирован, тогда для него существует 7 круговых перестановок, переходящих друг в друга при повороте. Эти перестановки не должны быть засчитаны, поэтому круговых перестановок из 7 элементов будет
. Если хоровод уже сформирован, тогда для него существует 7 круговых перестановок, переходящих друг в друга при повороте. Эти перестановки не должны быть засчитаны, поэтому круговых перестановок из 7 элементов будет  .
.
Размещения без повторений.
Определение 7: Пусть имеется  различных предметов. Расстановки из
различных предметов. Расстановки из  элементов по
элементов по 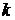 элементов (
элементов ( ) называются размещениями без повторений. Обозначают:
) называются размещениями без повторений. Обозначают:  . Здесь имеется в виду, что элементы в расстановках не повторяются.
. Здесь имеется в виду, что элементы в расстановках не повторяются.
В данном определении существенной является следующая позиция: две расстановки различны, если они отличаются хотя бы одним элементом или порядком элементов.
Приведем еще одно определение размещений, эквивалентное исходному, более простое для понимания.
Определение 8: Конечные упорядоченные множества называются размещениями.
Теорема 3: Количество всех размещений из  элементов по
элементов по 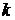 элементов без повторений вычисляется по формуле:
элементов без повторений вычисляется по формуле:
 . (2)
. (2)
Доказательство. Пусть имеется произвольное множество  , состоящее из
, состоящее из  элементов. Необходимо выбрать из этого множества
элементов. Необходимо выбрать из этого множества 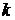 различных элементов. Причем, важен порядок выбора.
различных элементов. Причем, важен порядок выбора.
Выбор элементов осуществляется поэтапно. Первый элемент расстановки можно выбрать  различными способами. Тогда из оставшихся элементов множества
различными способами. Тогда из оставшихся элементов множества  второй элемент расстановки выбирается
второй элемент расстановки выбирается  способом. Для выбора третьего элемента возможно
способом. Для выбора третьего элемента возможно  способа и т.д. Тогда для выбора
способа и т.д. Тогда для выбора 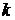 - го элемента имеем
- го элемента имеем  способ. Следовательно, согласно правилу умножения, количество таких расстановок будет равно:
способ. Следовательно, согласно правилу умножения, количество таких расстановок будет равно:
 .
.
По определению, такие расстановки являются размещениями. Что и требовалось доказать.
Пример 3: Собрание из 25 человек выбирает президиум из 3 человек: 1) председатель, 2) заместитель, 3) секретарь. Сколько возможно вариантов выбора президиума?
Решение. Выбирая трех человек из 25, замечаем, что важен порядок выбора, поэтому количество президиумов будет равно:
 .
.
Замечание: Число размещений без повторений можно также находить по формуле:
 . (3)
. (3)
Если в знаменателе дроби из формулы (3)  , то принято считать
, то принято считать  .
.
Замечание: Формула (3) отличается компактностью, но при решении задач удобнее использовать формулу (2). Дробь, стоящая в правой части формулы (3), может быть сокращена до целого числа. Это число равно числу из правой части формулы (2).
Пример 4: Сколько можно составить двухбуквенных слов (буквы не повторяются) из 33 букв русского алфавита?
Решение. В данном случае мы имеем дело не со словами в лингвистическом понимании, а с буквенными комбинациями произвольного состава.
Тогда количество различных комбинаций из 2 букв, выбранных из 33 букв алфавита, будет равно:
 .
.
В данном случае важен порядок букв. Если поменять 2 буквы в слове, то получим новое слово.
Замечание: Перестановка без повторений – это частный случай размещений без повторений при  . Можно сказать, что перестановка из
. Можно сказать, что перестановка из  элементов – это размещение из
элементов – это размещение из  элементов по
элементов по  элементов:
элементов:

В некоторых задачах по комбинаторике не имеет значения порядок расположения объектов в той или иной совокупности. Важно лишь то, какие именно элементы ее составляют. В таких ситуациях мы имеем дело с сочетаниями.
Сочетания без повторений.
Определение 9: Сочетания без повторений из  элементов некоторого множества по
элементов некоторого множества по 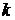 элементов (
элементов ( ) – это расстановки, отличающиеся друг от друга составом, но не порядком элементов. Обозначают:
) – это расстановки, отличающиеся друг от друга составом, но не порядком элементов. Обозначают:  (от французского слова combinaison – сочетание).
(от французского слова combinaison – сочетание).
В данном случае в расстановках важен состав, а не порядок элементов в подмножестве. Если две расстановки отличаются только порядком следования элементов, то с точки зрения сочетаний они не различимы. Элементы в этих расстановках не повторяются.
С точки зрения теории множеств определение сочетаний можно сформулировать иначе.
Определение 10: Конечные неупорядоченные множества называются сочетаниями.
Таким образом, сочетания – это такая выборка элементов, при которой их порядок совершенно не важен.
Сочетаний из  элементов по
элементов по 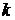 элементов должно быть меньше, чем соответствующих размещений. Это следует из того, что не надо засчитывать расстановки одинакового состава.
элементов должно быть меньше, чем соответствующих размещений. Это следует из того, что не надо засчитывать расстановки одинакового состава.
Теорема 4: Число сочетаний  находится по следующей формуле:
находится по следующей формуле:
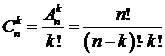 . (4)
. (4)
Доказательство. Если из произвольного  -элементного множества выбраны
-элементного множества выбраны 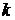 элементов, то их можно пронумеровать номерами
элементов, то их можно пронумеровать номерами  числом способов, равным
числом способов, равным  . Оставшиеся
. Оставшиеся  элементов можно занумеровать номерами
элементов можно занумеровать номерами  ,
,  , …,
, …,  всего
всего  способами. Кроме того, сам отбор
способами. Кроме того, сам отбор 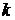 элементов из
элементов из  элементов можно осуществить
элементов можно осуществить  способами. Таким образом, мы получили
способами. Таким образом, мы получили  вариантов нумерации полного множества из
вариантов нумерации полного множества из  элементов, которых всего
элементов, которых всего 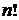 . Поэтому имеем
. Поэтому имеем  , откуда получаем:
, откуда получаем:
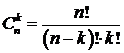 .
.
Теорема доказана.
Замечание: Дробь, стоящая в правой части (4), может быть сокращена до целого числа.
Из формулы числа сочетаний следует:
 ,
,  ,
,  .
.
Формула (4) может быть преобразована к виду:  . Отсюда видно, что число размещений
. Отсюда видно, что число размещений  в
в  раз больше числа соответствующих сочетаний
раз больше числа соответствующих сочетаний  . Другими словами, чтобы посчитать все сочетания
. Другими словами, чтобы посчитать все сочетания  , нужно исключить из всех размещений
, нужно исключить из всех размещений  подмножества, отличающиеся порядком (их будет
подмножества, отличающиеся порядком (их будет  штук), т.е.
штук), т.е.  делят на
делят на  .
.
Пример 5: Сколькими способами можно выбрать 3 различные краски из имеющихся пяти.
Решение. Порядок выбора красок не важен. Важно только какие краски выбраны. Поэтому количество вариантов равно:  .
.
Пример 6: Сколькими способами можно пошить трехцветные полосатые флаги, если имеется материал пяти различных цветов.
Решение. Порядок выбора полос важен, поэтому количество таких флагов равно: 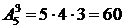 .
.
Свойства сочетаний.
Одной из наиболее распространённых комбинаторных формул является формула числа сочетаний. Для упрощения подсчётов и для доказательства некоторых утверждений удобно использовать следующие свойства сочетаний:
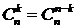 , (1)
, (1)
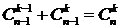 . (2)
. (2)
Доказательство. Используем формулу числа сочетаний.
1)  .
.
2)  .
.
Первое из доказанных свойств несет в себе своеобразную симметричность формулы для числа сочетаний. Например, 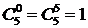 ,
,  . Это свойство упрощает вычисления.
. Это свойство упрощает вычисления.
Второе тождество иногда называют тождеством Паскаля. Оно позволяет разбивать  на классы
на классы  и
и  .
.
Числа  возникают в самых разных задачах комбинаторики и теории вероятностей. Например, из тождества Паскаля следует, что для всех натуральных чисел
возникают в самых разных задачах комбинаторики и теории вероятностей. Например, из тождества Паскаля следует, что для всех натуральных чисел  и
и 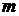 , причем
, причем  , справедливо равенство:
, справедливо равенство:
 . (3)
. (3)
Эта формула может быть доказана индукцией по числу слагаемых в левой части.
Рассмотрим некоторые прикладные аспекты последней формулы.
1) При 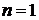 формула (3) превращается в известную формулу суммы первых
формула (3) превращается в известную формулу суммы первых 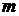 членов арифметической прогрессии:
членов арифметической прогрессии:
 .
.
Таким образом, можно вычислять сумму слагаемых натурального ряда от 1 до 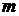 .
.
2) Для  из формулы (3) имеем:
из формулы (3) имеем:
 ,
,
или окончательно:
 .
.
Последняя формула дает возможность находить сумму квадратов чисел натурального ряда от 1 до  .
.
3) Для  получаем:
получаем:
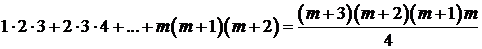 ,
,
или после преобразований:
 .
.
Таким образом, можно получить формулы для сумм более высоких степеней натуральных чисел.
Сочетания можно встретить и в школьном курсе математики. Например, в качестве коэффициентов бинома Ньютона выступают именно сочетания.
Бином – это сумма двух слагаемых, например, 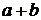 .
.
Формула бинома Ньютона в общем виде и её доказательство приводятся в следующей теореме.
Теорема 1: Для любых чисел  и
и  , и любого натурального числа
, и любого натурального числа  справедливо следующее равенство:
справедливо следующее равенство:
 . (4)
. (4)
Доказательство. Применим индукцию по числу  .
.
При 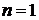 :
:  .
.
Пусть формула верна, для случая, когда степень бинома равна  . В этом случае следующее равенство будем считать выполненным:
. В этом случае следующее равенство будем считать выполненным:
 .
.
Покажем, что формула выполняется для  - й степени:
- й степени:
 .
.
Используя предыдущее равенство и раскрывая скобки, получим требуемое выражение.
В доказательстве можно также использовать свойство:  .
.
Формула (4) носит имя и математика Исаака Ньютона, хотя она была известна задолго до него, например, в Европе ее знал французский математик Блез Паскаль. Заслуга Ньютона состоит в том, что он нашел обобщение этой формулы на случай нецелых показателей. Тем не менее, приведенное выше разложение называют биномом Ньютона, а коэффициенты  называются биномиальными коэффициентами.
называются биномиальными коэффициентами.
Следствие: Рассмотрим некоторые частные случаи формулы бинома Ньютона:
1) если 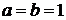 , то
, то  .
.
2) если  , то
, то  .
.
3) Сумма показателей степени при  и
и  в любом слагаемом разложения равна
в любом слагаемом разложения равна  .
.
4) Биномиальные коэффициенты, равноудаленные от концов разложения, равны между собой, так как 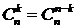 .
.
5) Биномиальные коэффициенты сначала возрастают, потом убывают.
Числовые значения биномиальных коэффициентов вычисляются по формуле числа сочетаний: 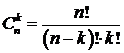 . Готовые значения этих коэффициентов располагаются в строках треугольника Паскаля.
. Готовые значения этих коэффициентов располагаются в строках треугольника Паскаля.
1 n = 0
1 1 n = 1
1 2 1 n = 2
1 3 3 1 n = 3
1 4 6 4 1 n = 4
1 5 10 10 5 1 n = 5
.........................
Треугольник Паскаля строится следующим образом. Боковые стороны состоят из единиц. Числа, находящиеся внутри, являются суммой вышестоящих чисел. Каждая строка треугольника соответствует некоторой степени для суммы  и содержит соответствующие биномиальные коэффициенты. Таким образом, для того, чтобы раскрыть степень суммы
и содержит соответствующие биномиальные коэффициенты. Таким образом, для того, чтобы раскрыть степень суммы  , нужно из треугольника Паскаля взять строку, соответствующую данному показателю степени
, нужно из треугольника Паскаля взять строку, соответствующую данному показателю степени  . Эта строка будет содержать нужные коэффициенты
. Эта строка будет содержать нужные коэффициенты  , к которым приписываются соответствующие буквенные выражения. Можно заметить, что строки треугольника Паскаля симметричны, поэтому достаточно взять только половину биномиальных коэффициентов и, если нужно, средний элемент.
, к которым приписываются соответствующие буквенные выражения. Можно заметить, что строки треугольника Паскаля симметричны, поэтому достаточно взять только половину биномиальных коэффициентов и, если нужно, средний элемент.
Замечание. При  , пользуясь треугольником Паскаля, получаем известную школьную формулу квадрата суммы:
, пользуясь треугольником Паскаля, получаем известную школьную формулу квадрата суммы:
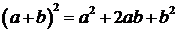 .
.
Аналогично, при  имеем формулу куба суммы:
имеем формулу куба суммы:
 .
.
Таким образом, можно записать разложение для любого значения показателя  .
.
Если требуется возвести в  - ю степень сумму более чем двух слагаемых, то такое выражение называется полиномом и является обобщением бинома Ньютона.
- ю степень сумму более чем двух слагаемых, то такое выражение называется полиномом и является обобщением бинома Ньютона.