Абрамсон стр. 1 12.12.2017
Конспект №4
Упражнение №1*.
Могут ли числа 2, 3, 5 быть членами (не обязательно соседними) одной геометрической прогрессии?
Упражнение №2.
Известно, что уравнение ах2+bx+c=0 имеет корни х1 и х2. Какие корни имеет уравнение сх2+bx+а=0?
Упражнение №3*.
Пусть уравнение х2+рx+q=0 имеет корни х1 и х2, а уравнение у2+ry+s=0 имеет корни y1 и y2. Выразите (у1-х1)(у1-х2)(у2-х1)(у2-х2) через p, q, r и s.
Полученный вами многочлен второй степени от четырёх переменных – коэффициентов квадратных трёхчленов, называется их результантом.
Он равен нулю тогда и только тогда, когда два трёхчлена имеют общий корень.
В некоторых случаях многочлен можно разложить в произведение многочленов первой степени, например Р(х)=(х-2)(2х-3)(1,5х+8) или Q(y)=(y-3)2(2y+5)3.
deg P(x)=3 и у него 3 корня: х=2, х=1,5 и х=- 
. deg Q(y)=5 и у него 2 корня: y=3 y=-2,5. Но если расписать Q(y)=(y-3)×(y-3)×(2y+5)×(2y+5)×(2y+5), то мы видим, что корень y=3 повторяется дважды, а корень y=-2,5 – трижды. Говорят, что y=3 – кратный корень кратности 2, а y=-2,5 - кратный корень кратности 3. Корни кратности 1 называются простыми. Сравните с разложением натуральных чисел на простые множители: 72=23×32.
Между прочим, если многочлен не разлагается в произведение других многочленов степени не меньше 1, то он тоже называется простым или примитивным.
Если считать корни вместе с их кратностями, то у многочлена 5-ой степени Q(y) их будет 5: 2 корня y=3 и 3 корня y=-2,5.
Упражнение №4.
Докажите (например, по индукции), что у многочлена степени n не может быть больше, чем n корней (считая корни с их кратностями).
Упражнение №5.
a) На склад привезли две одинаковые бочки раствора неизвестной (возможно, разной) концентрации. Необходимо добиться одинаковой концентрации в обеих бочках. Имеется третья пустая бочка и прибор, позволяющий переливать любое количество раствора из бочки в бочку.
Как добиться равной концентрации в обеих бочках?
b) На склад привезли три одинаковых бочки раствора неизвестной (возможно, разной) концентрации. Имеется ещё четвёртая пустая бочка и прибор, позволяющий переливать любое количество раствора из бочки в бочку. Необходимо добиться одинаковой концентрации во всех бочках.
Как это сделать?
c) На склад привезли n одинаковых бочек раствора неизвестной концентрации. Имеется ещё одна пустая бочка и прибор, позволяющий переливать любое количество раствора из бочки в бочку. Необходимо получить одинаковую концентрацию во всех бочках. Как этого добиться?
Упражнение №6.
Кузнечик прыгает по координатной прямой. Сначала он прыгает из точки с координатой 0 в точку с координатой 1, а потом произвольно – влево или вправо, но каждый его следующий прыжок вдвое больше предыдущего. Сможет ли он когда-либо вернуться в исходную точку?
Следующие задачи являются трудными и необязательными. Мы их, безусловно, когда-нибудь решим, а пока что я их предлагаю для свободного размышления. Кто решит – пусть объявит об этом и расскажет (получит, разумеется, 5). Знаний у вас достаточно, чтобы их решить, но требуется не простое применение этих знаний, а изрядная смекалка.
Задачи повышенной трудности.
Упражнение №7*.
Придумайте такую функцию, определённую на отрезке [-4,4], график которой переходил бы сам в себя при повороте на 90° вокруг начала координат (hint: remember, that functions need not to be continuous, their graphs can consist of separate pieces)
Упражнение №8*.
Решите систему уравнений:
(hint: from the first equation y³0,5. After substitution x into the second equation remember Bezout theorem)
Упражнение №9*.
Среди натуральных чисел, меньших 100, выбрали 51 различное число.
Докажите, что из них можно выбрать 6 таких чисел, что никакие два из выбранных не будут иметь одинаковых цифр ни в одном разряде.
(hint: use Dirichlet principle (or principle of boxes, drawer principle). One can find ten which holds 6 of these numbers. Continue.)
Упражнение №10*.
Решите в целых числах уравнение m(m+1)=n3. (hint: prove, that m=k3)
Составляя дерево возможностей (“если а, то или b или с или d”), определите,
Упражнение №11
Можно ли выписать 9 цифр 1,2,…,9 по кругу так, чтобы сумма никаких двух соседних цифр не делилась бы ни на 3, ни на 5, ни на 7?
Рассуждая логически (а не перебором всех возможных вариантов) и сводя к минимуму проверки возможных комбинаций,
Упражнение №12*
Определите порядок, в котором расположились в итоговой турнирной таблице 5 команд, если известно, что участник, предположивший, что они займут места в порядке
А, B, C, D и E не только не угадал место ни одной из команд, но даже ни одной пары следующих друг за другом команд! Другой же участник, предсказавший, что они займут места в порядке D, A, E, C и B угадал места двух команд и две пары следующих друг за другом команд.
Подробно опишите ход ваших рассуждений (важен не столько сам ответ, а и путь к нему)
Комбинаторика.
Комбинаторика изучает два типа задач. Первый тип – выяснить, существует ли конфигурация элементов в некотором множестве с заданными характеристиками.
Второй тип – определить число таких конфигураций или дать их классификацию.
Обычно число элементов в таких конфигурациях конечно.
Как это не удивительно, многие результаты комбинаторики основаны на всего двух вполне интуитивно очевидных (и легко формально доказываемых по индукции) правилах.
Правило суммы.
Пусть множество S состоит из m элементов, |S|=m, а множество Т состоит из n элементов, |T|=n и TÇS=Æ. Тогда |SÈT|=m+n.
Применяется оно в следующей ситуации: если нам необходимо выбрать один элемент либо из S, либо из T, то у нас имеется для этого m+n комбинаций.
Обобщение этого правила на несколько слагаемых звучит так: пусть T1,T2,…,Tn – разбиение множества М и |Ti|=ti, i=1,2,…,n. Тогда |M|= 
.
Правило произведения.
Пусть множество S состоит из m элементов, |S|=m, и для каждого элемента sÎS возможен выбор одного из n элементов множества Т (в котором может быть и более, чем n элементов). Тогда число всевозможных пар (s,t) равно m×n.
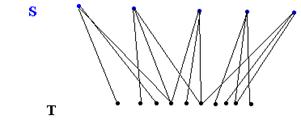Множество всех таких упорядоченных пар (s,t) обозначим M(S,T,n). Обобщённое правило произведения утверждает: если |T1|=n1, M2=M(T1,T2,n2), M3=M(M2,T3,n3),…,Mr=M(Mr-1,Tr,nr), то |Mr|=n1n2×…×nr.
Множество Mr представляет собой множество всевозможных последовательностей длины r (x1,x2,…,xr), где xiÎTi. Последовательность (x1,x2,…,xr) называют иногда кортежем. Если все Ti представляют собой одно и то же множество Т, то кортеж (x1,x2,…,xr) называют r-выборкой. Если при этом все элементы xi в r-выборке различны, то такую r-выборку называют r-перестановкой из n элементов.
Мы уже выяснили ранее, что число Р(n,r) r-перестановок из n элементов равно P(n,r)=n(n-1)…(n-r+1). Между прочим, это частный случай правила произведения, когда Т1=Т2=…=Тr n1=n, n2=n-1,…nr=n-r+1. В частности, Р(n,n)=n! Имеется ещё одно название и обозначение для r-перестановок из n элементов: размещения без повторений из n элементов по r. Их число, P(n,r) обозначается как 
(от слова “Arrangement”).
Размещения без повторений из n по n называются перестановками (permutation).
Перестановкой с повторениями называется любой кортеж длины n в котором каждый символ i встречается ni раз. Например, рассмотрим множество всех слов длины 8, состоящих из четырёх букв п, м, а, р. Тогда в слове «папамама» п и м встречаются по два раза, а – 4, р – ни одного. Если эти буквы занумеровать числами 1,2,3 и 4, то мы получим в нашем примере n=8, k=4, n1=n2=2, n3=4, n4=0. Если вместо букв использовать цифры, то последовательности длины n из k цифр 1, 2,…,k являются элементами множества An, где А={1,2,…,n}. Например, вместо «рамапара» мы написали бы 43231343 и при k=4, n=8 имели бы n1=1, n2=1, n3=4, n4=2. Заметим, что во всех словах n1+…+nk=n.
Множество всех перестановок с повторениями обозначим как S(n1, n2,…nk).
При k=n и n1=n2=…=nn=1 |S(1,…1)|=P(n,n)=n!.
Решая следующее упражнение, начните со случая (часто бывает полезно идти от простого к сложному), когда лишь одно из ni¹1.
Упражнение №13.
|S(n1, n2,…nk)|= 
Выведите отсюда полиномиальную теорему:
Упражнение №14
(x1+…+xk)n=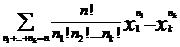 
При k=2 получаем старую, знакомую биномиальную теорему.
Впрочем, можно полиномиальную теорему вывести (по индукции) из биномиальной.
Неупорядоченные подмножества, состоящие из k элементов, данного множества из n элементов, называются сочетаниями без повторений из n элементов по k.
А теперь из биномиальной теоремы выведите следующий факт:
Упражнение №15.
Число всех подмножеств из k элементов во множестве из n элементов равно 
.
В упражнениях, в которых содержится некоторое утверждение, его надо доказать.
Упражнение №16.
Число всех пар (А,В) подмножеств множества {1,2,…,n} таких, что АÌВ, равно 3n.
Упражнение №17*.
Число решений уравнения x1+…+xk=n в натуральных числах равно 
. Например, число натуральных решений уравнения х+у+z=5 равно 
.
(Hint: make correspondence, for example: (3,2,2)®(001010); (2,4,1)®(010001) and reduce the problem to ex.#15)
Упражнение №18.
Число решений уравнения x1+…+xk=n в целых неотрицательных числах равно 
.
Числовые ответы в комбинаторных задачах обычно бывают велики. Поэтому их можно не вычислять в виде числа, записанного в своей десятичной записи, а оставлять в виде, например, произведения каких-то его делителей или формулы, содержащей биномиальные коэффициенты.
Упражнение №19.
Во скольких пятизначных числах все цифры различны?
Упражнение №20.
Каких чисел от 1 до 10 миллионов больше: тех, в 10-ой записи которых встречается 1, или тех, в которых её нет? (Answer is: number of those, where there is “1”, is greater)
Упражнение №21.
Параллельными прямыми на плоскости называются две прямые, которые либо совпадают, либо не имеют общих точек. Даны три различных точки, А, В и С. Из каждой провели по n прямых так, что никакие две из них не параллельны и никакие три из них не пересекаются в одной точке (кроме самих точек А, В и С). Найдите число точек пересечения данных прямых, не считая самих точек А, В и С. (Answer is 3n2)
Упражнение №22.
На плоскости провели 20 прямых, среди которых нет ни одной пары параллельных и ни одной тройки прямых, пересекающихся в одной точке. Найдите
а) число точек пересечения этих прямых; (190)
b) число треугольников, образованных этими прямыми. (2280)
Упражнение №23*.
На книжной полке стоит n книг. Сколькими способами можно выбрать из них k книг так, чтобы не брать две рядом стоящие книги? Применить ваш результат к случаю, когда надо выбрать таким образом 4 тома из 10-томного собрания сочинений. (35)
(Hint: reduce this problem to the problem of distributing k units among n-k zeros)
Формула включений и исключений.
Как вы, надеюсь, помните ещё из первого конспекта, если А и В – конечные множества, то |AÈB|=|A|+|B|-|AÇB|. Опираясь на этот результат и действуя по индукции, получите обобщение этой формулы на случай нескольких множеств:
Упражнение №24
|A1È…ÈAn|= 
- 
+ 
-…+(-1)n-1|A1ÇA2Ç…ÇAn|.
Характеристической функцией cA подмножества А универсального множества U называется функция, принимающая значение 1 на всех элементах множества А и принимающая значение 0 на всех остальных элементах множества U (т.е., на дополнении Ас множества А в U). Характеристическая функция самого U – это просто функция, тождественно равная 1, равно как характеристическая функция пустого множества тождественно равна нулю.
Из определения легко следует, что cAÇB(u)=cA(u)cB(u) и 
=1-cА
Для конечных множеств |A|= 
.
Пользуясь тем (кто забыл – см. конспект №1), что A1È…ÈAn= 
,
Упражнение №25
a) Дайте ещё одно (другим способом) доказательство формулы включений-исключений.
b) Покажите, что следующая задача (чаще всего употребляемая в приложениях) является просто иной формулировкой формулы включений-исключений:
пусть имеется N предметов, каждый из которых может обладать свойствами a1,…,an. Пусть N(aiaj…ak) означает число предметов, обладающих свойствами ai, aj,…,ak (и, может быть, ещё какими-то другими). Если же предметы не обладают каким-то свойством, то над этим свойством ставим черту. Например, 
означает число предметов, обладающих свойствами а1 и а2 и не обладающих свойствами а3 и а4.
Так вот, имеет место следующая формула:
Упражнение №26
В научно-исследовательском институте работают 67 человек. Из них 47 знают английский, 35 – немецкий и 20 - французский, 23 – знают английский и немецкий, 12 английский и французский, 11- немецкий и французский и 5 человек знают все три языка.
Сколько человек в этом институте не знают ни одного языка?
Упражнение №27
Староста одного класса дал следующие сведения об учениках:
«в классе учатся 45 школьников, в том числе 25 мальчиков. 30 учатся на «хорошо» и «отлично», в том числе 16 мальчиков. Спортом занимаются 28 учеников, среди которых 18 мальчиков и 17 школьников, которые учатся на «хорошо» и «отлично». Учатся на «хорошо» и «отлично» и в то же время занимаются спортом 15 мальчиков».
Достоверны ли эти сведения?
Упражнение №28
Сколько целых чисел от 0 до 999 не делятся ни на 2, ни на 3, ни на 5, ни на 7?
Упражнение №29
В составлении 40 задач для олимпиады школьников принимали участие 30 студентов со всех 5 курсов. Любые два студента с одного курса придумали равное количество задач, а любые два студента с разных курсов придумали разное количество задач. Сколько человек придумало одну задачу?
Упражнение №30*
a) Сколькими способами из последовательности 1, 2,…, 2n можно извлечь три числа, являющихся тремя последовательными членами одной арифметической прогрессии? (n(n-1))
b) Тот же вопрос для последовательности 1, 2,…, 2n+1. (n2)
(Hint: find out, how many solutions has inequality a+2d£2n)
Упражнение №31
Сколько двузначных чисел в сумме с числом, записанном теми же цифрами в обратном порядке, даёт полный квадрат?
Упражнение №32
Четыре числа сложили всеми возможными способами по два и получили шесть сумм: 2, 4, 9, 9, 14 и 16. Найдите эти числа.
Упражнение №33*
В математическом кружке занимаются 6 учеников. За некоторое время каждый из них был на занятиях 7 раз, каждые двое встретились там 5 раз, каждые трое – 4 раза, каждые четверо – 3 раза, каждые пять 2 раза и все шесть – 1 раз. Каждый отсутствовал на уроках 8 раз. Сколько занятий было за это время? Сколько раз учитель сидел в одиночестве?
Упражнение №34.
Сколькими способами можно навесить 5 колец на 8 гвоздей, если на один гвоздь не навешивать более одного кольца?
Упражнение №35.
Сколькими способами можно выбрать из полной колоды карт, содержащей 52 карты, по одной карте каждой масти?
А если все они должны быть различными (т. е., чтобы не было двух королей или двух десяток, например)?
Упражнение №36.
Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли бить друг друга?
Упражнение №37.
На званый вечер приглашены пять мужчин и пять женщин. Напротив каждого места на стол необходимо поставить табличку с именем того, кто будет на этом месте сидеть. При этом лица одного пола не должны сидеть рядом.
Сколькими способами можно расставить таблички?
Упражнение №38.
У мамы два одинаковых яблока, 3 одинаковых мандарина и 4 одинаковых апельсина. Каждый день в течение 9 дней подряд она выдаёт сыну по одному фрукту. Сколькими способами она может это сделать?
Упражнение №39*.
Пусть Mr – число размещений без повторений из m элементов по r, а Nr – число размещений без повторений из n элементов по r. Докажите, что число размещений из m+n элементов по r задаётся формулой (M+N)r, в которой, после возведения в степень, надо заменить все показатели индексами.
Упражнение №40*.
Докажите, что при n³2 и |x|£1 (1+x)n+(1-x)n£2n.
Упражнение №41.
Укротитель хочет вывести на арену 5 львов и 4 тигров, при этом два тигра не должны идти рядом. Сколькими способами он может расположить зверей?
(Put intervals in between any two lions, before and after them)
Упражнение №42.
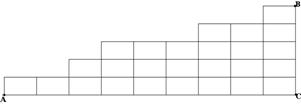Из плит 30´50см строится лестница, ведущая из точки А в точку В.
АС=4,5м, ВС=1,5м. Высота каждой ступеньки должна быть ровно 30см, а её длина кратна 50см. Сколькими способами можно построить лестницу?
(This problem one also can reformulate, coding each stairs by 1 and 0: put 0 when broken line goes right and 1 where it goes up. Thereafter one can reduce this problem to the previous one).
За круглым столом короля Артура сидят 12 рыцарей. Сколькими способами можно выбрать из них 5 рыцарей, которые не враждовали бы друг с другом, если каждый рыцарь враждует только с двумя своими соседями по столу?
Чтобы свести эту задачу к предыдущим, надо разорвать круглую цепочку рыцарей так, чтобы они уже образовывали ряд. Для этого надо выбрать какого-нибудь рыцаря и рассмотреть два случая: когда он входит в команду из 5 рыцарей (а, значит, оба его соседа не входят) и когда, наоборот, он в неё не входит. А теперь
Упражнение №43.
Решите эту задачу.
Упражнение №44.
Выведите следующие два свойства треугольника Паскаля:
a)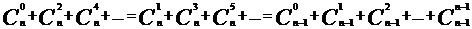 
b) При переходе к следующей строке треугольника Паскаля сумма чисел в строке удваивается. 
Упражнение №45.
Докажите, что 
=3n.
Напишите и обоснуйте естественное обобщение этой формулы.
Рассмотрим сочетания без повторений из n элементов а1,а2,…,аn. Сочетаний из k элементов будет 
и в них, поэтому, будет всего k× элементов (если каждый элемент считать заново в каждом из этих сочетаний). С другой стороны, если элемент входит в некоторое сочетание а1 а2а3а4, то остальные входящие в это сочетание элементыобразуют уже сочетание из n-1 элемента. Каждый из этих остальных элементов (кроме уже выбранного элемента) может, как входить в какое-либо сочетание вместе с этим фиксированным элементом, так и не входить в него.
Пользуясь этими наводящими соображениями, докажите, что
Упражнение №46*.
Теперь рассмотрим сочетания с повторениями – число комбинаций длины m из предметов n+1 типа. Скажем, различных слов длины m в алфавите из n+1-ой буквы.
Мы уже знаем, что их 
. Разобьём их на классы Кi по числу вхождений первой буквы. Так, в класс К0 она не входит, в класс К2 входит два раза и т.д.
Пользуясь этим разбиением, докажите, что
Упражнение №47.
Упражнение №48.
Выведите из предыдущего упражнения формулу
Упражнение №49.
Выведите из предыдущего упражнения формулы:
1+2+…+m= 
(A)
1×2+2×3+…+m(m+1)= 
(B)
1×2×3+2×3×4+…+m(m+1)(m+2)= 
(C)
Упражнение №50.
Замечая, что n2=n(n+1)-n и используя формулы (А) и (В), выведите формулу
12+22+…+m2= 
(D)
Упражнение №51.
Действия по образцу и подобию предыдущего упражнения, выведите формулу
13+23+…+m3= 
(Е)
Рассмотрим теперь сочетания без повторений из n элементов по m. Назовём опять эти n элементов буквами и разобьём их на два типа, «гласных» и «согласных». Пусть в первый тип входят p букв, а во второй – n-p соответственно. Тогда каждое сочетание можно характеризовать количеством входящих в него гласных букв.
Используя эту интерпретацию, выведите формулу:
Упражнение №52.
Упражнение №53.
Получите из предыдущей формулы формулу
.
В частности, 
Снова возьмём алфавит из n букв и разобьём его на р гласных и n-p согласных. Составим всевозможные сочетания с повторениями из n букв.
Разобьём их на классы, отнеся к k-му классу слова, содержащие k гласных.
Используя это разбиение, выведите формулу:
Упражнение №54.
Используя упражнение 125а из конспекта №3 и замены p®p+1; n®n+2 и m®m-n, получите отсюда тождество:
Упражнение №55.
Обобщите эти тождества, рассмотрев буквы не двух (гласные-согласные), а q типов, например, q цветов, причём одноцветные буквы различаются ещё и шрифтом. Букв i-го типа имеется ni экземпляров. Составляя из них всевозможные сочетания без повторений из m элементов, разобьём их на классы, характеризуя класс набором целых неотрицательных чисел (m1,m2,…,mq); 0£mi£ni; m1+m2+…+mq=m.
Вспомнив правило произведения, получите тождество:
Упражнение №56.
, гдеn1+n2+…+nq=n
Упражнение №57.
Докажите тождество: 
.
Упражнение №58.
Выведите из предыдущего тождества тождество 
Упражнение №59.
Докажите тождество: 
Упражнение №60.
Докажите, что
a) 
;
b) 
;
c) 
;
d) 1+14 
Упражнение №61.
Докажите тождество:
Используя формулу a+b+…+x+y= ((a+b+…+x+y)+(y+x+…+b+a)):2, вычислите суммы:
Упражнение №62.
a) 
;
b) 
;
c) 
Упражнение №63.
a) 
;
b) 
;
c)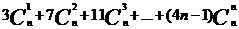 
Упражнение №64.
a) 
;
b) 
c) 
Упражнение №65.
a) 
;
b) 
Вероятность.
Def. Конечное множество Е={e1,e2,…,en} назовём пространством элементарных событий, элементы (точки) ei, i=1,…,n этого множества назовём элементарными событиями, если на этом множестве задана неотрицательная функция, называемая вероятностью, такая, что 
.
Подмножества множества Е называются событиями, и вероятность события является (по определению) суммой вероятностей составляющих его элементарных событий.
Упражнение №66.
Из цифр 1, 2, 3, 4 и 5 выбирается сначала одна цифра, а затем вторая. Предположим, что все 20 возможных исходов равновероятны.
Каковы вероятности того, что
a) в первый раз будет выбрана нечётная цифра;
b) во второй раз будет выбрана нечётная цифра;
c) оба раза будут выбраны нечётные цифры?
Упражнение №67.
Монета бросается до тех пор, пока два раза подряд она не выпадет одной и той же стороной. Каждому возможному исходу, состоящему из n бросаний, припишем вероятность, равную 2-n. Какова вероятность того, что опыт закончится до 6-го бросания?
Упражнение №68.
Три игрока a, b и c играют в настольный теннис. В первом туре играют a и b, во втором туре победитель играет с с, в третьем – победитель с проигравшим в первом туре и т.д. (проигравший в следующей партии не играет). Турнир продолжается до тех пор, пока один из игроков не выиграет двух партий подряд. Ничьи исключаются. Возможные исходы турнира описываются схемой: аа, aсс, acbb, acbaa, bb, bcc, bcaa,…
Каждому элементарному событию, состоящему из последовательности, длиной k букв, припишем вероятность 2-k. Докажите, что вероятность того, что победитель не определится до k-го тура, равна 2-k+1.
Упражнение №69.
На шести гранях кости-кубика написаны цифры от 1 до 6. При бросании кубика считаем выпадение каждой грани равновероятным (равным 
). Какова вероятность того, что при 6 бросаниях 1 не выпадет ни разу?
Упражнение №70.
В СШАкаждый из 50 штатов представлен в сенате двумя сенаторами.В комитет из 50 сенаторов случайным образом[1]выбирают сенаторов. Какова вероятность того, что в этом комитете не будет ни одного из двух сенаторов от штата Юта?
Упражнение №71.
Бросаем r пронумерованных шаров случайным образом в n ящиков. Какова вероятность того, что в заданном ящике окажется ровно k шаров (0£k£r)?
Упражнение №72.
Будем теперь считать шары неразличимыми, так что характеристикой размещения шаров по ящикам служит набор чисел {r1, r2, …rn}, где ri – это число шаров в i-ом ящике; 0£ri£r и r1+r2+…+rn=r. Для случая распределения 6 шаров по 6 ящикам
А) определите вероятность того, что в каждом ящике окажется ровно по одному шару;
В) определите наиболее вероятное распределение шаров по ящикам.
Упражнение №73.
Пусть имеются n шаров двух цветов: n1 белых и n2=n-n1 чёрных. Выбираем из них r шаров. Какова вероятность того, что среди выбранных шаров окажется ровно k белых?
Упражнение №74.
Применим результат, полученный в предыдущем упражнении к следующей задаче.
Из озера выловили 1000 рыб. Их пометили и отпустили опять в озеро. Через некоторое время выловили снова 1000 рыб. 100 из них оказались помеченными. Какова наиболее вероятная оценка числа рыб, живущих в озере? Обобщите задачу, считая неизвестное число рыб в озере n, число пойманных при первом улове рыб (играющих роль белых шаров) n1, число пойманных при втором улове рыб r, число меченых рыб k. Пусть qk(n) обозначает вероятность того, что во втором улове оказалось ровно k помеченных рыб.
Выясните, при каком n достигается максимум qk(n) при данном k, посчитав, до каких пор отношение qk(n):qk(n-1) будет больше 1 (то есть, функция qk(n) возрастает).
Упражнение №75.
Сколькими способами можно поставить на шахматной доске две ладьи так, чтобы они били друг друга?
Упражнение №76.
Буквы азбуки Морзе образуются как последовательности точек и тире. Сколько букв можно составить из последовательностей длины не более, чем в 5 символов?
Упражнение №77.
Сколько различных костяшек домино можно образовать, используя числа 1, 2,…,n?
Упражнение №78.
Случайным образом (т.е., с равной вероятностью) расставляются в ряд числа 1, 2,…,n.
Какова вероятность того, что
a) числа 1 и 2 окажутся рядом и именно в этом порядке;
b) числа 1, 2 и 3 окажутся рядом и именно в этом порядке.
числа 1 и 2 окажутся рядом и именно в этом порядке
Упражнение №79 [2].
Каковы вероятности того, что среди трёх выбранных наугад цифр окажутся
a) три одинаковых;
b) две одинаковых;
c) все три разных?
Упражнение №80.
У человека имеется n ключей, из которых только один подходит к замку.
Он последовательно испытывает их. Докажите, что с одинаковыми вероятностями этот процесс может закончиться после первого, второго, …, n-го испытаний.
Упражнение №81.
В городе с населением в n+1 человек некто узнал новость. Он через день рассказывает о ней первому встречному, тот через день – другому первому встречному и так далее. Каждый человек, впервые узнавший новость, передаёт её в течение следующих суток любому из остальных n человек с одинаковой вероятностью.
Каковы вероятности того, что
a) в течение r дней новость не возвратится к тому, кто узнал о ней первым;
b) новость не возвратится ни к кому, кто о ней уже знал.
Во многих случаях мы имеем дело с событиями, которые могут закончиться одним из двух исходов. Подброшенная монета может упасть орлом или решкой, стрелок может попасть или промахнуться, ученик в тесте может выбрать правильный ответ или неправильный и т.д. Опыт, который может закончиться одним из двух вариантов, называется испытанием Бернулли. Например, если обозначать один из исходов буквой У, а другой Н, то после трёх испытаний по схеме Бернулли, мы можем получить следующие элементарные события: УНН, УНУ, ННН и т.д. Допустим, что вероятность исхода «У» равна при каждом испытании q, а вероятность «Н» равна q (q+p=1).
Упражнение №82.
Чему равна вероятность события «НУН» в серии из трёх испытаний Бернулли?
Упражнение №83.
Чему равна вероятность появления двух «У» в серии из 5 испытаний Бернулли?
Упражнение №84.
Остап Бендер играет против членов шахматного клуба на 6 досках. Вероятность выигрыша у него – 0,75. Какова вероятность того, что Остап Бендер победит не менее, чем в 5 поединках?
Упражнение №85.
Некто решил провести лотерею. Для этого он изготовил 100 билетов и объявил, что один из них является выигрышным с выигрышем в 500р, а на 10 других выдаётся выигрыш по 100 рублей. Остальные 89 билетов ничего не выигрывают. По какой минимальной цене должен устроитель продавать свои билеты, если он хочет заработать не менее 1000 рублей, а проведение самой лотереи стоит тоже 1000 рублей?
Эта задача подходит нас к следующим определениям.
Def. Функция Х:Е®Q, заданная на пространстве Е элементарных событий, называется случайной величиной.
Пример. Пусть пространство Е={e1,e2,e3,e4,e5} состоит из 5 элементарных событий с вероятностями р(е1)=р1=0; р(е2)=р2=0,5; р(е3)=р3=0,25; р(е4)=р4=р5=0,125.
Пусть Х(е1)=Х(е2)=3, Х(е3)=-2, Х(е4)=Х(е5)=-1. Эта случайная величина принимает три значения: -1, -2 и 3. Теперь определим другую функцию, называемую распределением случайной величины Х. Еёзададим на множестве значений случайной величины Х.
В нашем случае такой областью было всё множество рациональных чисел Q, хотя только три из них действительно являлись образами каких-то элементов из Е. На всех остальных числах положим рХ(t)=0. На этих же значениях посмотрим, чему равны вероятности соответствующих множеств. рХ(3)=Р(Х=3)=р1+р2=0,5. рХ(-1)=Р(Х=-1)=р4+р5=0,25. рХ(-2)=Р(Х=-2) =р3=0,25. График функции распределения нашей случайной величины в итоге получился таким:
Понятно, что сумма значений функции распределения любой случайной величины равняется 1 – ведь это сумма вероятностей всех элементарных событий вероятностного пространства Е. Просто все Е разбивается на подмножества, соответствующие каждому значению случайной величины и берутся вероятности этих подмножеств (как суммы вероятностей входящих в них элементарных подмножеств).
Пусть случайная величина Х принимает ровно k значений х1,…,хk с вероятностями р(Х=хi)=pi соответственно. Математическим ожиданием случайной величины Х называют число Е(Х)= 
.
В случае, когда речь идёт, например, об игре и хi – эта сумма выигрыша, а рi – его вероятность, то Е(Х) имеет смысл вероятности общего выигрыша. Какой смысл в этом случае приобретают отрицательные значения хi?
Упражнение №86.
a) Чему равно математическое ожидание Е(Х) если все значения случайной величины Х равновероятны?
b) Найдите Е(Х) для случайной величины, принимающей все целые значения от -15 до 15 с равными вероятностями;
c) Найдите распределение и математическое ожидание случайной величины, равной сумме очков, выпавших при двух бросаниях игральной кости;
d) Найдите распределение и математическое ожидание случайной величины, равной числу клеток в подбитом корабле противника в результате первого выстрела при игре в морской бой.
Случайные величины, как и любые функции можно складывать и умножать на числа. Пусть Х и У – две случайные величины, а с – число.
Упражнение №87.
a) Докажите, что Е(сХ)=сЕ(Х) и Е(Х+У)=Е(Х)+Е(У);
b) Примените доказанные факты к решению следующей задачи.
Игроки по очереди подбрасывают игральную кость, и затем продвигают фишку на столько клеток вперёд по игровому полю, сколько очков выпало на кости. Найдите математическое ожидание случайной величины, равной числу клеток, на которые продвинется фишка после 10 бросков.
c) Симметричную монету бросили 5 раз. Найдите математическое ожидание случайной величины, равной числу выпавших орлов.
d) Пусть S – число успехов в серии из n испытаний Бернулли с вероятностью успеха р. Найдите Е(S).
Во многих вычислениях мы исп