ЗАДАНИЕ 1. Для двойного интеграла 
:
1) сделать чертеж области интегрирования D, ограниченной заданными линиями 
;
2) в повторных интегралах расставить пределы интегрирования в том и другом порядке;
3) вычислить массу неоднородной пластины D, если поверхностная плотность в каждой ее точке ρ (х, у) = х.
РЕШЕНИЕ. 1) Область интегрирования D ограничена полуокружностью х = 
и прямыми 
. Построим область интегрирования D (рисунок 1).
Рисунок 1 – Чертеж области интегрирования
Найдем координаты точки А, точки пересечения прямой у = 2 х и полуокружности х = . Для этого решим систему уравнений
Подставив х = 
во второе уравнение системы, получим у = 2. Подставив значение у = 2 в любое из двух уравнений, найдем х = 1. Итак, точка А имеет координаты А (1; 2).
2) Расставим пределы интегрирования в повторных интегралах в том и другом порядке.
Если выбрать внешнее интегрирование по у, а внутреннее по х, то область интегрирования D правильная (стандартная) в направлении оси Ох, так как всякая прямая, параллельная оси Ох и проходящая через внутренние точки области, пересекает ее границы только в двух точках. Точки входа лежат на прямой х = 
, а точки выхода лежат на полуокружности х = 
.
Таким образом, получим
= 
.
Для того чтобы расставить пределы интегрирования в другом порядке, проведем через область D прямые, параллельные оси Оу. Эти прямые пересекают сначала ось Ох, затем прямую у = 2 х или дугу полуокружности у = 
. Следовательно, линией входа будет у = 0 (0 ≤ х ≤ 
), а линиями выхода будут у = 2 х (0 ≤ х ≤ 1) и у = (1 ≤ х ≤ ). Так как линия выхода задается двумя различными аналитическими выражениями, то область D необходимо разбить прямой х = 1 на две области, и повторный интеграл будет равен сумме интегралов по каждой из этих областей (свойство аддитивности).
Таким образом, получим
= 
.
3) Вычислим массу неоднородной пластины D, если поверхностная плотность в каждой ее точке ρ (х, у) = х. Масса плоской пластины D с плотностью ρ (х, у) равна двойному интегралу от плотности m = 
m = 
.
Вычислим сначала внутренний интеграл по переменной х, а затем внешний по переменной у, имеем:
m = = 
= 
=
= 
= 
= 
= 
.
Ответ: т = .
ЗАДАНИЕ 2. С помощью тройного интеграла вычислить объем тела, ограниченного заданными поверхностями x 2 + y 2 = 1, y – 2 z = 2, z = 0. Сделать схематический чертеж.
РЕШЕНИЕ. Объём тела V вычислим по формуле
,
где V – тело, ограниченное данными поверхностями. Изобразим тело V схематически (рисунок 2). Данное тело ограничено цилиндрической поверхностью x 2 + y 2 = 1, снизу – плоскостью y – 2 z = 2, а сверху – плоскостью z = 0. Проекцией тела 
на плоскость 
является круг x 2 + y 2 = 1, радиуса R = 1 (рисунок 3). Целесообразно перейти в тройном интеграле от декартовых прямоугольных координат к цилиндрическим координатам по формулам:
Тогда уравнение цилиндра в этих координатах примет вид r = 1, уравнения плоскостей – 
, а 
В области V координаты r, φ, z изменяются так: 0 ≤ r ≤ 1, 0 ≤ φ ≤ 2π, 
– 1 ≤ z ≤ 0. Вычисление тройного интеграла 
сведём к вычислению трёхкратного интеграла 
.
Вычисления проведём в три этапа:
1) 
2) 
;
3) 
(ед3).
Рисунок 2 – Чертеж тела V
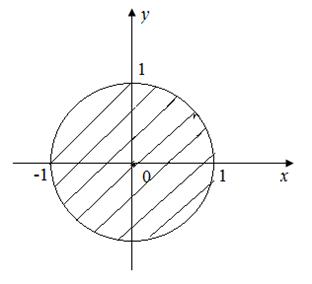
Рисунок 3 – Проекция тела V на плоскость
Ответ: V = π ед3.
ЗАДАНИЕ 3