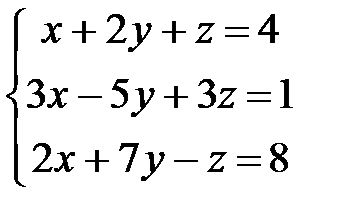Пусть вершины треугольника имеют координаты: А (1; 1), В (5; 3), С (3; 6).
1. Чтобы выписать уравнения всех сторон треугольника, воспользуемся уравнением прямой, проходящей через две заданные точки с координатами (x 0, y 0) и (x 1, y 1):
 .
.
Таким образом, подставляя вместо (x 0, y 0) координаты точки А, а вместо (x 1, y 1) координаты точки В, мы получим уравнение прямой АВ:
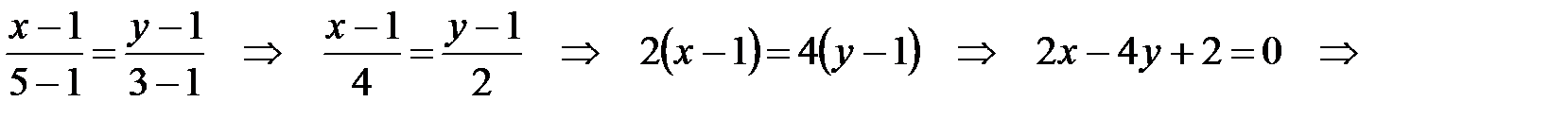

Полученное уравнение будет уравнением прямой АВ, записанным в общей форме. Аналогично находим уравнение прямой АС:


И так же уравнение прямой ВС:
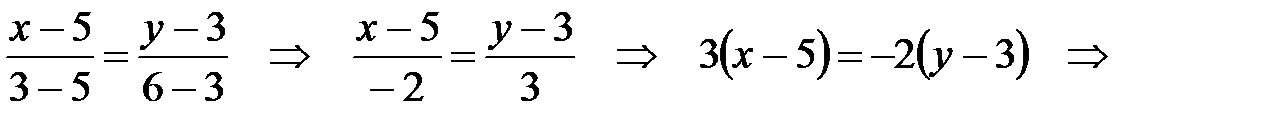
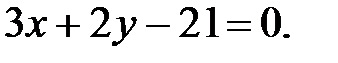
2. Заметим, что множество точек треугольника АВС представляет собой пересечение трех полуплоскостей, причем каждую полуплоскость можно задать с помощью линейного неравенства. Если мы возьмем уравнение любой из сторон ∆ АВС, например АВ, тогда неравенства
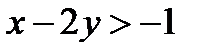 и
и 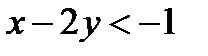
задают точки, лежащие по разные стороны от прямой АВ. Нам нужно выбрать ту полуплоскость, где лежит точка С. Подставим ее координаты в оба неравенства:
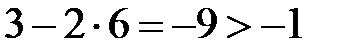 и
и  .
.
Правильным будет второе неравенство, значит, нужные точки определяются неравенством
 .
.
Аналогично поступаем с прямой ВС, ее уравнение 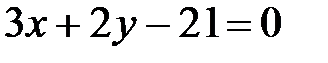 . В качестве пробной используем точку А (1, 1):
. В качестве пробной используем точку А (1, 1):
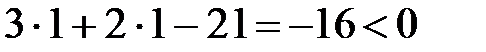 ,
,
значит, нужное неравенство имеет вид:
 .
.
Если проверим прямую АС (пробная точка В), то получим:
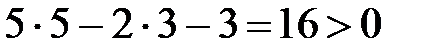 ,
,
значит, нужное неравенство будет иметь вид

Окончательно получаем систему неравенств:
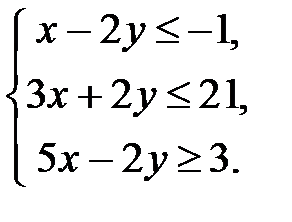
Знаки «≤», «≥» означают, что точки, лежащие на сторонах треугольника, тоже включены во множество точек, составляющих треугольник АВС.
3. а) Для того, чтобы найти уравнение высоты, опущенной из вершины А на сторону ВС, рассмотрим уравнение стороны ВС:  . Вектор с координатами
. Вектор с координатами  перпендикулярен стороне ВС и, значит, параллелен высоте. Запишем уравнение прямой, проходящей через точку А параллельно вектору
перпендикулярен стороне ВС и, значит, параллелен высоте. Запишем уравнение прямой, проходящей через точку А параллельно вектору  :
:


Это уравнение высоты, опущенной из т. А на сторону ВС.
б) Найдем координаты середины стороны ВС по формулам:
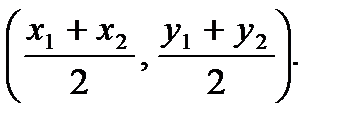
Здесь  – это координаты т. В, а
– это координаты т. В, а  – координаты т. С. Подставим и получим:
– координаты т. С. Подставим и получим:

Прямая, проходящая через эту точку и точку А является искомой медианой:


в) Уравнение биссектрисы мы будем искать, исходя из того, что в равнобедренном треугольнике высота, медиана и биссектриса, опущенные из одной вершины на основание треугольника, равны. Найдем два вектора 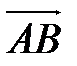 и
и  и их длины:
и их длины:
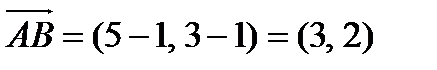 ,
, 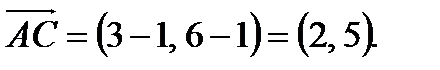
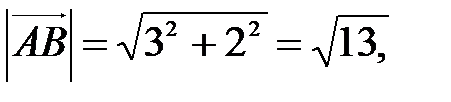

Тогда вектор 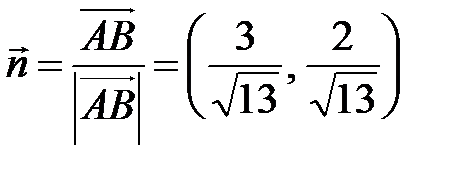 имеет такое же направление, что и вектор
имеет такое же направление, что и вектор 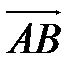 , а его длина
, а его длина 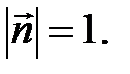 Точно так же единичный вектор
Точно так же единичный вектор 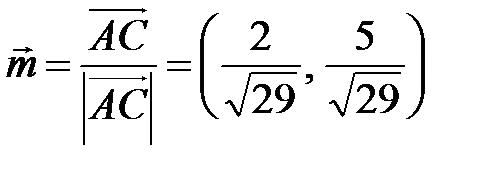 совпадает по направлению с вектором
совпадает по направлению с вектором  Сумма векторов
Сумма векторов

есть вектор, который совпадает по направлению с биссектрисой угла А. Таким образом, уравнение искомой биссектрисы можно записать виде:
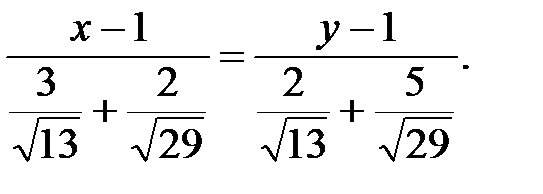
4) Уравнение одной из высот мы уже построили. Построим уравнение еще одной высоты, например, из вершины В. Сторона АС задается уравнением  Значит, вектор
Значит, вектор  перпендикулярен АС, и, тем самым, параллелен искомой высоте. Тогда уравнение прямой, проходящей через вершину В в направлении вектора
перпендикулярен АС, и, тем самым, параллелен искомой высоте. Тогда уравнение прямой, проходящей через вершину В в направлении вектора 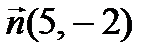 (т. е. перпендикулярно АС), имеет вид:
(т. е. перпендикулярно АС), имеет вид:
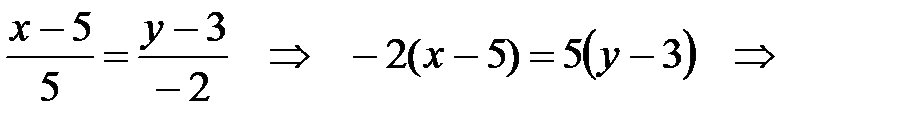
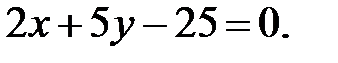
Известно, что высоты треугольника пересекаются в одной точке. В частности, эта точка является пересечением найденных высот, т.е. решением системы уравнений:

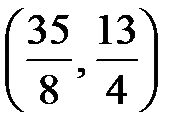 - координаты этой точки.
- координаты этой точки.
5. Середина АВ имеет координаты  . Запишем уравнение медианы к стороне АВ. Эта прямая проходит через точки с координатами (3, 2) и (3, 6), значит, ее уравнение имеет вид:
. Запишем уравнение медианы к стороне АВ. Эта прямая проходит через точки с координатами (3, 2) и (3, 6), значит, ее уравнение имеет вид:

Заметим, что ноль в знаменателе дроби в записи уравнения прямой означает, что эта прямая проходит параллельно оси ординат.
Чтобы найти точку пересечения медиан достаточно решить систему уравнений:
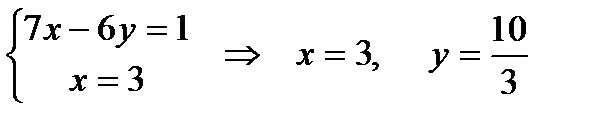 .
.
Точка пересечения медиан треугольника имеет координаты  .
.
6. Длина высоты, опущенной на сторону АВ, равна расстоянию от точки С до прямой АВ с уравнением  и находится по формуле:
и находится по формуле:

7. Косинус угла А можно найти по формуле косинуса угла между векторами 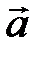 и
и 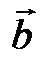 , который равен отношению скалярного произведения этих векторов к произведению их длин:
, который равен отношению скалярного произведения этих векторов к произведению их длин:
 :
:

Задачи № 11-20
Дана система уравнений: 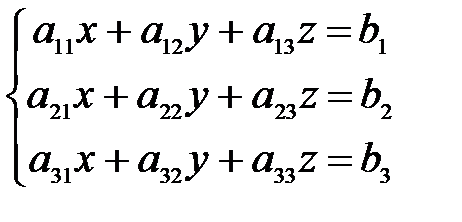 .
.
1. Решить ее тремя способами:
· методом Гаусса,
· по формулам Крамера
· с помощью обратной матрицы.
2. Записать разложение вектора 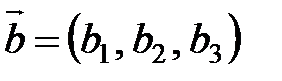 по базису, составленному из векторов
по базису, составленному из векторов 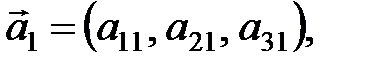
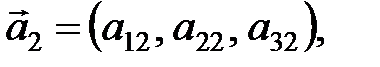
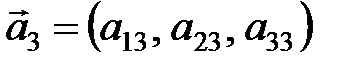 . Ответ обосновать.
. Ответ обосновать.
11. 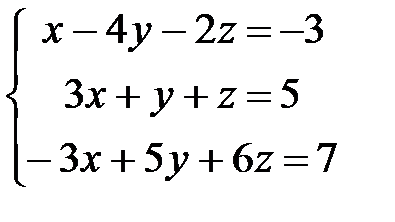
12. 
13. 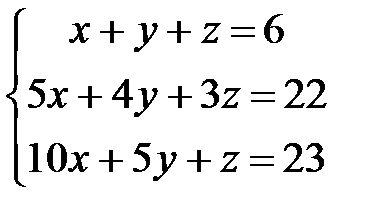
14. 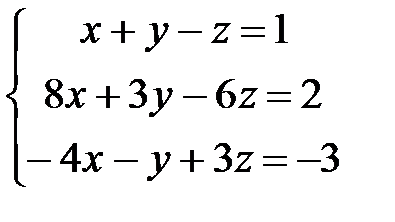
15. 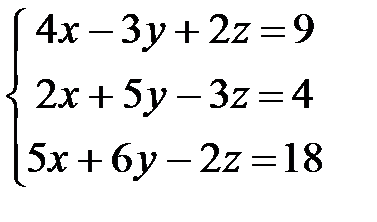
16. 
17. 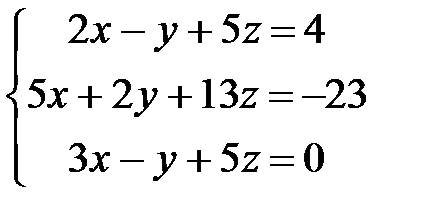
18. 
19. 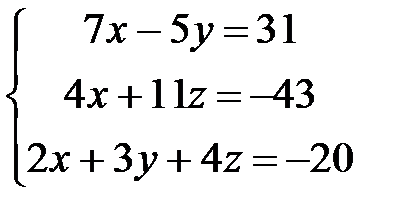
20.