Любая неубывающая последовательность, ограниченная сверху, - сходящаяся.
Любая невозрстающая последовательность, ограниченная снизу, - сходящаяся.
Док-во: (для неубывающей) Для Xn£Xn+1 для "n. Так как последовательность ограничена, то существует число А такое, что выполняется неравенство Xn£А для "n. Рассмотрим множество Х, состоящее из элементов последовательности {Xn}. По условию это множество ограничено сверху и не пусто. Þ Множество Х имеет точную верхнюю грань. Обозначим ее через А и докажем, что А – предел {Xn}.
Так как А – точная верхняя грань множества Х, то для "e>0 найдется номер N такой, что XN >A - e. Так как последовательность {Xn} неубывающая, то при "n>N имеем Xn>A - e. С другой стороны, Xn£A<A+e для "n. Т. о., при "n>N получаем неравенство A - e<Xn<A+e, т. е. |Xn – A|< e при "n>N. Þ А – предел последовательности {Xn}.
ЗАМ: ограниченность монотонной последовательности является необходимым и достаточным условием сходящейся последовательности.
12. Число е.
ТЕОР2: Рассмотрим последовательность Xn= 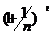 и докажем, что эта последовательность сходящаяся и ее предел равен е.
и докажем, что эта последовательность сходящаяся и ее предел равен е.
Док-во: Докажем, что она сходится. Для этого достаточно доказать, что она возрастающая и ограниченная сверху.
1) Докажем, что последовательность {Xn} возрастающая, т. е. для "n Xn<Xn+1.
(1+1/n)  разложим по формуле бинома Ньютона.
разложим по формуле бинома Ньютона.
Xn = (1+1/n)  = 1+(n/1!) ·(1/n)+(n ·(n – 1)/2!) ·(1/n
= 1+(n/1!) ·(1/n)+(n ·(n – 1)/2!) ·(1/n  )+(n ·(n – 1) ·(n – 2)/3!) ·(1/n
)+(n ·(n – 1) ·(n – 2)/3!) ·(1/n  )+K+(n ·(n – 1) ·(n – 2)) ·K·(n – (n – 1))/n!) ·(1/n
)+K+(n ·(n – 1) ·(n – 2)) ·K·(n – (n – 1))/n!) ·(1/n  ) = 2+(1/2!) ·(1 – 1/n)+(1/3!) ·(1 – 1/n) ·(1 – 2/n)+K+(1/n!) ·(1 – 1/n) ·(1 – 2/n) ·K·(1 – (n – 1)/n)
) = 2+(1/2!) ·(1 – 1/n)+(1/3!) ·(1 – 1/n) ·(1 – 2/n)+K+(1/n!) ·(1 – 1/n) ·(1 – 2/n) ·K·(1 – (n – 1)/n)
Аналогично для Xn+1. Для любого 0<k<n выполняется соотношение (1 – 1/k)<(1 – 1/(k+1)). Þ Ввыражении для Xn+1 каждое слагаемое больше, чем соответствующее слагаемое в выражении для Xn. Þ Xn< Xn+1 для любого n. Þ {Xn} – возрастающая последовательность.
2) Докажем, что последовательность {Xn} – ограничена сверху. Рассмотрим выражение для Xn. Так как 1/k!<1/2 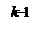 при k>2, то Xn<2+1/2!+1/3!+…+1/n!<1+1+1/2+1/4+1/8+…+1/2
при k>2, то Xn<2+1/2!+1/3!+…+1/n!<1+1+1/2+1/4+1/8+…+1/2 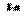 =1+(1 – 1/2
=1+(1 – 1/2  )/(1 – 1/2) = 1+2(1 – 1/2
)/(1 – 1/2) = 1+2(1 – 1/2  ) = 3 – 1/2
) = 3 – 1/2 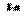 <3. Þ Для "n 2<Xn<3 и последовательность {Xn} ограничена сверху. По Т о мон огр последовательности она является сходящейся. Ее предел на бесконечности Эйлер обозначил через е.
<3. Þ Для "n 2<Xn<3 и последовательность {Xn} ограничена сверху. По Т о мон огр последовательности она является сходящейся. Ее предел на бесконечности Эйлер обозначил через е.
ОПР1: Число е – иррациональное, это число не может быть корнем никакого алгебраического уравнения с целыми коэффициентами. Такие иррациональные числа называются трансцендентными.
13. Теорема о вложенных промежутках.
ТЕОР1: Для любой последовательности вложенных отрезков существует единственная точка, принадлежащая всем этим отрезкам.
14. Понятие функции и способы ее задания.
ОПР1: Если для любого элемента хÎХ поставлен в соответствие по закону f единственный элемент уÎУ, то на множестве Х задана функция y=f (x), причем х – независимая переменная (аргумент), все значения х – область определения функции D (f); совокупность всех значений функции f (x) – область значений функции Е(f).
ОПР2: Функцию, D(f) и E(f) которой являются числовые множества, называют числовой функцией одной действительной переменной.
ОПР3: Графиком функции f(x) является множество точек плоскости, абсцисса которых равна аргументу, а ордината равна значению функции.
ОПР4: Графиком числовой функции f, заданной на числовом промежутке Х, называется множество G всех точек координатной плоскости, имеющих вид М(х; f(х)), где хÎХ, т.е. {(х; у): у=f(х); хÎХ}.
ОПР5: Функция задана аналитически, если закон, устанавливающий соответствие между множествами всех значений аргумента и функции, задается формулой.
Преимущества: сжатость, компактность задания, можно вычислить значение функции для любого значения аргумента из области определения, можно применить к данной функции аппарат мат анализа.
ОПР6: Табличный способ задания заключается в задании таблицы определенных значений аргумента и соответствующих им значений функции.
ОПР7: При графическом способе задания функции соответствие между аргументом и функцией задается посредствам графика.
Преимущества: наглядность, что делает его чрезвычайно полезным при изучении функции.
ОПР8: Пусть заданы две функции y = f(x) и z = F(y), при чем D(F)ÉE(f), тогда для любого хÎХ соответствует zÎZ, где z = F(y), y = f(x), значит z=F(f(x)). Эта функция, определяемая соответствием называется сложной функцией или суперпозицией функций f и F.
ОПР10: Всякая функция, которая задана явным образом с помощью формулы, содержащей конечное число арифметических операций и суперпозиций элементарных функций называется элементарной функцией. D(f) = R для основных элементарных функций, при которых данная функция имеет смысл; E(f) - тоже вещественные числа.
ОПР9: Классификация функций. Это основные элементарные функции.
1) Степенная: у = 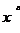 .
.
2) Показательная: у =  .
.
3) Логарифмическая: у = 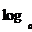 x.
x.
4) Тригонометрические.
5) Обратные тригонометрическим.
6) y = const.
1)Многочлены (полиномы): Р(Х)=А0+А1*Х+А2* 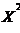 + …+Аn*
+ …+Аn* 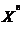
2)Рациональные R(x) = 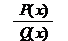 , P(x) и Q(x) – многочлены.
, P(x) и Q(x) – многочлены.
3) Алгебраические, которые заданы с помощью суперпозиции рациональных функций, степенных с иррациональным показателем и арифметических действий.
4) Трансцендентные –элементарные функции, которые не являются алгебраическими. Все тригонометрические, обратные им, показательная, логарифмическая.
15. Предел функции в точке.
ОПР1: (Г) Число B называется пределом функции У = F(Х) в точке А (или при Х®А), если для любой последовательности значений аргумента Х1, Х2,…, Хn,…, сходящейся к А и состоящей из чисел Хn, отличных от А, соответствующая последовательность значений функции F(X1), F(X2),…,F(Xn),… сходится к числу B. ("{Xn}®A, XnÎX, Xn¹A):{F(Xn)}®B
ОПР2: (К) Число B называется пределом функции У = F(Х) в точке А (или при Х®А), если для любого положительного числа e найдется отвечающее ему положительное число d, зависящее от e, такое, что для всех значений аргумента Х, удовлетворяющего условию 0<|X – A|<d, справедливо неравенство |F(X) – B|<e.
("e>0)($ d=d(e)>0)("xÎX:0<|x – A|<d):|F(x) – B|<e
ОПР3: (Г) Число B называется правым (левым) пределом функции У = F(Х) в точке А (или при Х®А), если для любой последовательности значений аргумента {Хn}, сходящейся к А и состоящей из чисел Хn, больших (меньших) А, соответствующая последовательность значений функции F(Xn) сходится к числу B. ("{Xn}®A, XnÎX, Xn>A):{F(Xn)}®B
("{Xn}®A, XnÎX, Xn<A):{F(Xn)}®B
ОПР4: (К) Число B называется правым (левым) пределом функции У = F(Х) в точке А (или при Х®А), если для любого положительного числа e найдется отвечающее ему положительное число d, зависящее от e, такое, что для всех значений аргумента Х, удовлетворяющего условию А<X<А+d (А - d<X<А), справедливо неравенство |F(X) – B|<e.
("e>0)($ d=d(e)>0)("xÎX:А<x<А+d):|F(x) – B|<e
("e>0)($ d=d(e)>0)("xÎX:А - d<x<А):|F(x) – B|<e
ТЕОР1: Функция f(x) имеет предел в точке А тогда только тогда, когда в этой точке существуют как правый, так и левый пределы, и оно равны. В этом случае предел функции равен односторонним пределам.
Док-во: Пусть правый и левый пределы f(x) равны В. Тогда (по опр прав и лев предела) для ("e>0) ($d1>0 и d2>0) ("X) удовлетворяющих условию A-S1<X<A и A<X<A+S2, выполняется условие |f(x)–B|<S. Возьмем d=min{d1,d2}. Тогда для "X, удовлетворяющих условию 0<|X – A|<S, будет выполняться неравенство |f(x) – B|<S. Þ lim f(x)=B в точке А.
ОПР5: (Г) Число B называется пределом функции У = F(Х) при Х®¥, если для любой бесконечно большой последовательности значений аргумента {Хn} соответствующая последовательность значений функции {F(Xn} сходится к числу B.
("{Xn}®A, XnÎX):{F(Xn)}®B
ОПР6: (К) Число B называется пределом функции У = F(Х) при Х®¥, если для любого положительного числа e найдется отвечающее ему положительное число d, зависящее от e, такое, что для всех значений аргумента Х, удовлетворяющего условию |X|>d, справедливо неравенство |F(X) – B|<e. ("e>0)($ d=d(e)>0)("xÎX:|x|>d):|F(x) – B|<e
ОПР7: (Г) Число B называется пределом функции У = F(Х) при Х®+¥ (при Х® - ¥), если для любой бесконечно большой последовательности значений аргумента {Хn}, все элементы которой положительны (отрицательны), соответствующая последовательность значений функции {F(Xn} сходится к числу B.
("{Xn} – б-б, XnÎX, Xn>0):{F(Xn)}®B
("{Xn} – б-б, XnÎX, Xn<0):{F(Xn)}®B
ОПР8: (К) Число B называется пределом функции У = F(Х) при Х®+¥ (при Х®- ¥), если для любого положительного числа e найдется отвечающее ему положительное число d, зависящее от e, такое, что для всех значений аргумента Х, удовлетворяющего условию X>d (X<d), справедливо неравенство |F(X) – B|<e.
("e>0)($ d=d(e)>0)("xÎX:x>d):|F(x) – B|<e
("e>0)($ d=d(e)>0)("xÎX:x<d):|F(x) – B|<e
16. Теорема о пределах функции.
ТЕОР1: Пусть две функции f(x) и g(x) заданы на одном множестве и имеют пределы в точке А, равные В и С. Тогда функции f(x)+g(x), f(x) – g(x), f(x)*g(x), f(x)/g(x) имеют в точке А пределы равные В+С, В – С, В*С, В/С (при С¹0).
Док-во: Пусть {Xn} – произвольная, сходящаяся к А последовательность, все элементы которой отличны от А. Последовательности {f(Xn)} и {g(Xn)} сходятся к пределам В и С (опр. предела Ф. по Г). Тогда последовательности {f(Xn)+g(Xn)}, {f(Xn) – g(Xn)}, {f(Xn)·g(Xn)}, {f(Xn)/g(Xn)} сходятся к пределам В+С, В – С, В·С, В/С (С¹0). Þ Функции f(x)+g(x), f(x) – g(x), f(x)·g(x), f(x)/g(x) имеют в точке А пределы равные В+С, В – С, В·С, В/С (С¹0).
ТЕОР2: Пусть функции f(x), g(x) и h(x) определены в некоторой окрестности точки А, за исключением, быть может, самой точки А, и функции f(x) и h(x) имеют предел в точке А, равный В. Пусть, кроме того, выполняется неравенство f(x)£g(x) £h(x) для всех хÎХ. Тогда предел функции g(x) в точке А равен В.
Док-во: Пусть {Xn} – произвольная, сходящаяся к А последовательность значений аргумента функций f(x) и h(x), все элементы которой отличны от А. Последовательности {f(Xn)} и {h(Xn)} сходятся к пределу В. Используя неравенства f(x)£g(x) £h(x) для "nÎN. Но тогда последовательность {g(Xn)} сходятся к пределу В. Þ lim g(x)=B в точке А.
17. I замечательный предел.
ТЕОР1: Предел функции g(x) =  в точке х = 0 существует и равен 1, т.е. lim
в точке х = 0 существует и равен 1, т.е. lim  =1
=1
n®¥
Док-во: Рассмотрим дугу окружности радиуса R=1 с центральным углом, радиальная мера которого равна Х (0<X<p/2).
 Тогда АО=1, sin X=MK, tg X=AT.
Тогда АО=1, sin X=MK, tg X=AT.
Площадь треугольника ОАМ меньше площади сектора ОАМ, которая меньше площади треугольника ОАТ, или 1/2ОА·МК<1/2OA·AM<1/2OA·AT Þ 1/2sin X<1/2X<1/2tg X Þ sin X<X<tg X. Разделим эти неравенства на sin X>0, получим 1< 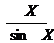 <
<  . Для обратных величин справедливы обратные неравенства cosX<
. Для обратных величин справедливы обратные неравенства cosX< 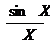 <1.
<1.
Так как неравенства справедливы при 0<X<p/2 Þ они справедливы и при -p/2<X<0, так как при замене Х на –Х все три функции cosX, (sin X)/X и 1 не меняют своих значений. Т. о. неравенства справедливы при всех ХÎ(-p/2, p/2), за исключением точки Х=0.
Так как обе функции f(x)=cosX и h(x)=1 имеют в точке Х=0 предел равный 1, то g(x)= 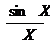 тоже имеет в точке Х=0 предел равный 1.
тоже имеет в точке Х=0 предел равный 1.
18. II замечательный предел.
ТЕОР1: Предел функции f(x) =  при х®¥ существует и равен числу е, т.е. lim
при х®¥ существует и равен числу е, т.е. lim  = e.
= e.
х®¥
Док-во: Пусть X>1.
Положим n=[x] (целая часть Х), тогда X=n+a, где n – натуральное число, а a удовлетворяет условию 0£a<1. Так как n£X<n+1, 1/(n+1)<1/X£1/n и 1+1/(n+1)<1+1/X£1+1/n, то (по свойству возрастания показательной Ф. с основанием, большим 1) 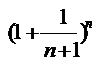 <
<  <
<  . При Х®+¥ (n®¥) lim
. При Х®+¥ (n®¥) lim  =lim
=lim 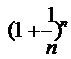 ·lim
·lim  =e·1=e и lim
=e·1=e и lim 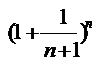 =[lim
=[lim 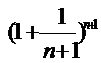 ]/[lim
]/[lim 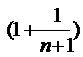 ]=e. Þ lim
]=e. Þ lim  =e.
=e.
Пусть теперь X<-1, X= -Y.
Тогда lim  =lim
=lim  =lim
=lim 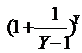 =lim
=lim  ·lim
·lim  = e·1=e
= e·1=e
(при X® -¥, Y® +¥).
Окончательно имеем lim  = e.
= e.
19. Бесконечно малые функции. Действия над ними.
ОПР1: Функция называется бесконечно малой в точке х=А (или при х®А), если предел этой функции в точке А равен 0.
ОПР2: (К) Функция a(х) называется бесконечно малой в точке х=А (или при х®А), если для любого положительного числа e >0 существует d>0 такое, что для всех хÎХ, удовлетворяющих условию 0<|x – A|<d, выполняется неравенство |a(x)|<e.
("e>0)($d=d(e)>0)("xÎX,0<|x – A|<d):|a(x)|<e
ОПР3: (Г) Функция a(х) называется бесконечно малой в точке х=А (или при х®А), если для любой сходящейся к А последовательности {Xn} значений аргумента Х, отличных от А, соответствующая последовательность значений функции {a(Xn)} является бесконечно малой. ("{Xn}®A, Xn¹A):{F(Xn)} – б-м
ТЕОР1: Для выполнения равенства limf(x)=b необходимо и достаточно, чтобы функция
х®¥
a(х)=f(х) - b была бесконечно малой при х®a.
Док-во:Необходимость: пусть limf(x)=b. Рассмотрим разность a(х)=f(х) – b и докажем, что a(х) – бесконечно малая функция при х®a. Действительно lim a(х)=lim(f(х) – b)=limf(x) – lim b=b – b=0.
Достаточность: Пусть a(х)=f(х) – b, где a(х) – бесконечно малая функция при х®a. Докажем, что limf(x)=b. Так как f(x)=b+a(х), то limf(x)= lim(b+a(х))= lim b+ lim a(х) =b+0=b.
ТЕОР2: Алгебраическая сумма и произведение конечного числа бесконечно малых функций при х®а, а также произведение бесконечно малой функции на ограниченную являются бесконечно малыми функциями при х®а.
Док-во: Вытекает из определения предела функции по Гейне и свойств бесконечно малых последовательностей.
20. Бесконечно большие функции. Связь с бесконечно малыми.
ОПР1: (К) Функция А(х) называется бесконечно большой в точке х=А (или при х®А), если для любого положительного числа e >0 существует d>0 такое, что для всех хÎХ, удовлетворяющих условию 0<|x–A|<d, выполняется неравенство |А(x)|>e.
("e>0)($d=d(e)>0)("xÎX,0<|x – A|<d):|A(x)|>e
ОПР2: (Г) Функция А(х) называется бесконечно большой в точке х=А (или при х®А), если для любой сходящейся к А последовательности {Xn} значений аргумента Х, отличных от А, соответствующая последовательность значений функции {A(Xn)} является бесконечно большой.
("{Xn}®A, Xn¹A): {F(Xn)} – б-б
ТЕОР1: Функция обратная бесконечно малой является бесконечно большой и наоборот.
Док-во: Пусть f(x) – бесконечно малая функция, т. е. ее предел равен 0. Пусть e>0, так как f(x) – бесконечно малая, то для 1/e>0 ($d=d(e)>0) ("xÎX, x¹A, |x-A|<d): |f(x)|<1/e Þ при этих условиях |1/f(x)|>e. ("e>0) ($d=d(A)>0) ("xÎX, x¹A, |x-A|<d): |1/f(x)|>e Þ 1/f(x) – бесконечно большая функция и ее предел равен ¥.
21. Сравнение бесконечно малых функций. Сравнение бесконечно больших функций.
ОПР1: Говорят, что a(х) является в точке А бесконечно малой функцией более высокого по
рядка, чем b(х), если lim 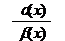 =0. a=о(b)
=0. a=о(b)
х®А
ОПР2: Говорят, что a(х) и b(х) являются в точке А бесконечно малыми функциями одного порядка, если lim 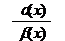 =А.
=А.
х®А
ОПР3: Говорят, что a(х) и b(х) являются в точке А эквивалентными бесконечно малыми функциями, если lim 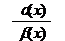 =1. a(х)~b(х)
=1. a(х)~b(х)
х®А
ЗАМ: Аналогичны правила для бесконечно больших функций. Справедливы для х®А+, ®А-, +¥, - ¥, ¥.
ТЕОР2: Если a(х) и b(х) бесконечно малые функции, то a(х) * b(х) = о(a(х)) и a(х) · b(х) = о(b(х)).
Док-во: lim (a(x)·b(x))/a(x)=lim b(x)=0, так как b(x) – бесконечно малая функция Þ a(х)·b(х) = о(a(х)) (a(х) · b(х) - более высокого порядка, чем a(х))
lim (a(x) ·b(x))/b(x)=lim a(х)=0, так как a(х) –бесконечно малая функция Þ a(х) · b(х) = о(b(х)) (a(х) · b(х) - более высокого порядка, чем b (х))
ТЕОР3: Если a(х) ~ a1(х) и b(х) ~ b1(х) бесконечно малые функции и х®А, то существуют lim 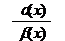 и lim
и lim  , причем они равны.
, причем они равны.
х®А х®А
Док-во: lima1(x)/b1(x)=lim(a1(x)/a(x))·(a(x)/b(x)))·(b(x)/b1(x))=lim(a1(x)/a(x))·lim(a(x)/b(x))·lim(b(x)/b1(x))= =1·lim(a(x)/b(x))·1=lim(a(x)/b(x))
22. Определение непрерывной функции в точке, на отрезке. Определение кусочно-непрерывной функции.
ОПР1: Функция f(x) называется непрерывной в точке А, если lim f(x) =f(A).
х®А
ЗАМ: Если f(x) непрерывна в точке А, то она определена и существует в точке А.
Если lim x =A, то lim f(x) = f(A) = f(lim x).
х®А х®А х®А
ОПР2: (Г) Функция f(x) называется непрерывной в точке А, если для любой последовательности значений аргумента {Xn} сходящейся к А соответствующая последовательность значений функции {F(Xn)} сходится к числу F(A). ("{Xn}®A, XnÎX): {F(Xn)}®F(A)
ОПР3: (К) Функция f(x) называется непрерывной в точке А, если для любого e >0 найдется отвечающее ему положительное число d такое, такое для всех х, удовлетворяющих условию
|x - A|< d,выполняется неравенство |f(x) – f(A)|<e.
("e >0)($d=d(e)>0)("xÎC:|x – A|<d):|f(x) – f(A)|<e
ОПР4:Приращение функции в точке А – Df = f(x) – f(a), приращение аргумента - Dх = х – а
ОПР5: Функция f(x) называется непрерывной в точке А, если ее приращение в этой точке является бесконечно малой функцией при Dх®0, lim Dy = 0.
Dх®0
ОПР6: Если lim f(x) = f(А), то функция f(x) непрерывна в точке А справа.
х®А+
ОПР7: Если lim f(x) = f(А), то функция f(x) непрерывна в точке А слева.
х®А -
ТЕОР1: Функция f(x) непрерывна в точке А, если она непрерывна в точке А справа и слева.
ОПР8: Функция называется кусочно-непрерывной на сегменте [A, B], если она непрерывна во всех внутренних точках сегмента за исключением конечного числа точек, в которых имеет разрыв I рода и, кроме того, существуют односторонние пределы в точках А и В.
ОПР9: Функция называется непрерывной на числовой прямой, если она кусочно-непрерывна на любом отрезке этой прямой.
23. Теорема о сумме, произведении, частном непрерывных функций.
ТЕОР2: Пусть функции f(x) и g(x) непрерывны в точке А. Тогда функции f(x) ± g(x), f(x) · g(x), f(x) ¤g(x) (при g(A)¹0) также непрерывны в этой точке.
Док-во: Так как функции f(x) и g(x) непрерывны в точке А, то lim f(x)=f(A) и lim g(x)=g(A) при х®А. Тогда пределы функций f(x) ± g(x), f(x) · g(x), f(x) ¤g(x) существуют и равны f(А) ± g(А), f(А) · g(А), f(А) ¤g(А) (при g(A)¹0). Но эти величины равны значениям функций в точке А. Þ f(x) ± g(x), f(x) · g(x), f(x) ¤g(x) непрерывны в точке А.
24. Точки разрыва функции.
ОПР1: Точка А называется точкой разрыва функции f(x), если f(x) в этой точке не является непрерывной функцией.
ОПР2: Классификация разрывов: