КВАНТОВАЯ МЕХАНИКА
Цель данной главы - установить ответы на следующие вопросы:
а) В каких случаях движение частиц можно описывать классически на основании законов Ньютона и когда необходимо для описания движения частиц использовать уравнение Шредингера?
б) Как находить энергетические уровни системы?
в) Как решать задачи об отражении и прохождении частиц через потенциальные барьеры?
г) Как распределен электрический заряд в атоме?
Ответы на эти вопросы строятся на двух уровнях: первый – можно дать физическое описание ситуации: представить систему уравнений с граничными и начальными условиями к ним. Первый уровень овладения материалом позволит перейти к изучению следующих глав и сделает возможным решение задач под руководством наставника. Второй - можно описать ситуацию физическими уравнениями, зная, как найти решения в предельных случаях, зная, как найти приближенное решение в произвольном случае и как построить процедуру уточнения приближенного решения. Второго уровня – уровня творческого овладения квантовой механикой – невозможно достичь на основе только данного пособия, для этого нужно подробно изучить ту литературу, которая дана в ссылках.
1.1 Волновая функция
Эксперименты по дифракции частиц на монокристаллах достаточно хорошо интерпретируются, если описать налетающую частицу плоской волной
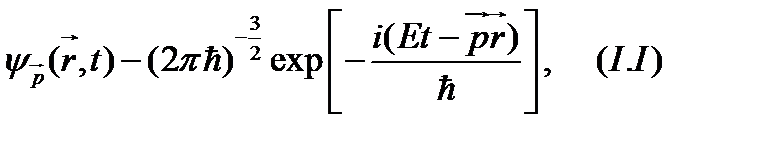
и далее, если вычислить дифракционную картину на экране хорошо известными из оптики методами, основанными на принципе Гюйгенса-Френеля, то частице следует приписать длину волны

и частоту


Такое рассмотрение позволяет нам частично ответить на первый вопрос, заданный в начале главы: квантовомеханическое описание необходимо в тех случаях, когда длина волны налетающий частицы соизмерена с характерным размером рассеивателя. Например, расстоянием, на котором происходит характерное изменение потенциала взаимодействия.
Далее постулируется, что вероятность местонахождения частицы dW определяется квадратом амплитуды


где dV- элемент объема.
Таким образом, величина  определяет плотность вероятности. Условие нормировки
определяет плотность вероятности. Условие нормировки  - функции.
- функции.

следует из того, что интегрируя по всему объему, мы получаем вероятность нахождения частицы в данном объеме, т.е. вероятность достоверного события.
Принцип суперпозиции постулирует:
«Если система частиц может находиться как в состоянии, определяемой функции  , так и состоянии
, так и состоянии  ,то она может находиться в таком состоянии
,то она может находиться в таком состоянии  , что
, что

где 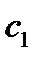 и
и  - произвольные константы».
- произвольные константы».
В общем случае

Если  различаются бесконечно мало (случай непрерывного спектра), то вместо суммы будем иметь интеграл, формула (I.5) представляет особый интерес, когда
различаются бесконечно мало (случай непрерывного спектра), то вместо суммы будем иметь интеграл, формула (I.5) представляет особый интерес, когда  образует полный набор функций
образует полный набор функций

 - дельта функции Дирака.
- дельта функции Дирака.
Пусть  - функция, описывающая систему, состоящую из одной частицы. Представим ее в виде интеграла Фурье
- функция, описывающая систему, состоящую из одной частицы. Представим ее в виде интеграла Фурье
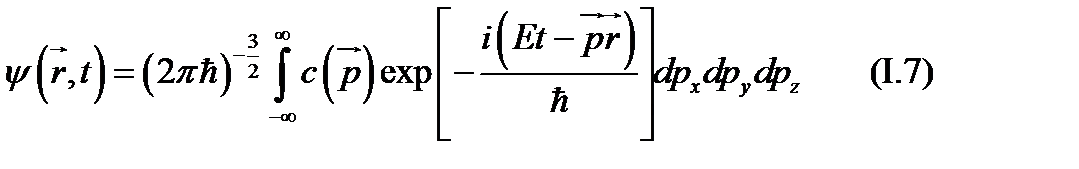
Сравнение формулы (I.7) и (I.5) позволяет утверждать, что квадрат  представляет собой плотность вероятности нахождения частицы в состоянии с импульсом
представляет собой плотность вероятности нахождения частицы в состоянии с импульсом  . При этом говорят, что функции
. При этом говорят, что функции

реализуют импульсное представление  функции.
функции.
В соответствии с тем, что 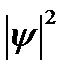 есть плотность вероятности, среднее значение любой физической функции данной системы определится формулой
есть плотность вероятности, среднее значение любой физической функции данной системы определится формулой

1.2 Операторы, собственные функции, собственные значения
Первоочередная задача настоящего параграфа состоит в нахождении вида функции F  , которые после подстановки в (I.8) определяет средние значения физических величин, дающих полное описание системы.
, которые после подстановки в (I.8) определяет средние значения физических величин, дающих полное описание системы.
Воспользуемся в качестве основного подхода методом индукции. Выберем в качестве известного частного случая плоскую волну (I.I) и определим среднее значение координаты

Интеграл (I.9) расходится. Это отражает то очевидное обстоятельство, что плоская волна не является локальным объектом, координата ее полностью не определена.
Займемся отысканием среднего значения импульса. В данном случае мы сразу знаем ответ: импульс частицы, которая описывается плоской волной (I.I), равен  . Произведение
. Произведение 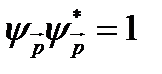 .
.
Отсюда угадывается вид F в формуле (I.8) для того, чтобы  .
.
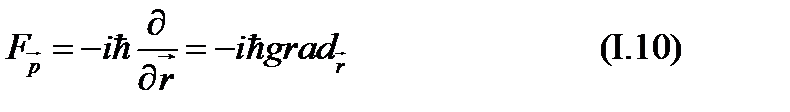
Заметим, что более принято не обозначение  , а
, а 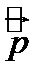 , эта величина носит название оператора импульса.
, эта величина носит название оператора импульса.
Упражнение I.1. Найдите вид оператора энергии, т.е. вид FE так чтобы  - энергии частицы.
- энергии частицы.
Это подсказывает нам, что и другие более сложные физические величины должны задаваться операторами.
Под оператором  мы будем подразумевать символ, показывающий, каким образом каждой из рассматриваемого класса функций U(x) сопоставляется другая функция V(x) из этого же класса
мы будем подразумевать символ, показывающий, каким образом каждой из рассматриваемого класса функций U(x) сопоставляется другая функция V(x) из этого же класса
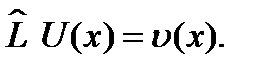
В квантовой теории рассматриваются только линейные самосопряженные операторы.
Линейность 
Самосопряженность или эрмитовость
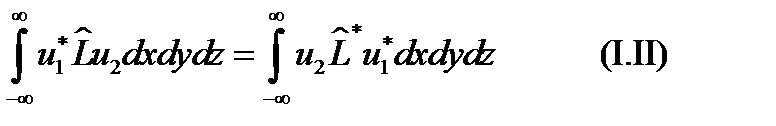
Существенно, что произведение операторов зависит от порядка сомножителей
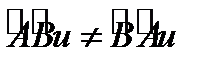
или в общем случае 
Если  , то операторы называют коммутирующими, а
, то операторы называют коммутирующими, а  носит название коммутатора операторов
носит название коммутатора операторов  и
и  .
.
В соответствии с (I.8) среднее значение физической величины L, определяемой оператором  , можно найти по формуле
, можно найти по формуле

Вычислим среднеквадратичное отклонение  как среднее значение оператора
как среднее значение оператора 
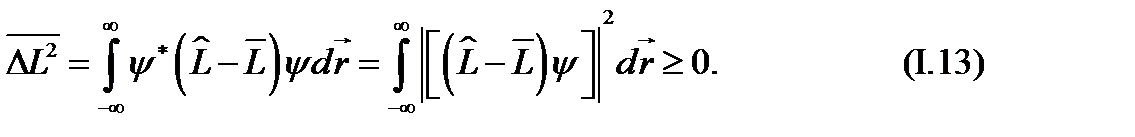
Последнее равенство есть следствие эрмитовости оператора  , условие (I.II).
, условие (I.II).
Найдем такие состояния 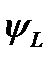 , в которых L имеет единственное значение
, в которых L имеет единственное значение  так, чтобы
так, чтобы  . Из уравнения (I.13) следует, что указанные условия удовлетворяются, если
. Из уравнения (I.13) следует, что указанные условия удовлетворяются, если 
 есть оператор, поэтому соотношение (I.14) является уравнением (например, дифференциальным).
есть оператор, поэтому соотношение (I.14) является уравнением (например, дифференциальным).
Решение этого уравнения будет определено единственным образом, если заданы начальные и граничные условия. При фиксации условий (I.14) может иметь нетривиальные решения  только при определенных значениях
только при определенных значениях 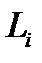 . Соответствующие решения называют собственными функциями, а
. Соответствующие решения называют собственными функциями, а 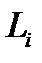 - собственными значениями оператора
- собственными значениями оператора  .
.
Требования, которые накладывает условие сохранения числа частиц на собственные функции во всей области изменения аргумента:
а) конечность,
б) непрерывность,
в) однозначность,
ведет к тому, что во многих случаях решения, удовлетворяющие указанным трем требованиям, существуют лишь при некоторых значениях L.
Считается, что можно наблюдать на опыте только те значения величины L, которые являются собственными значениями оператора  .
.
Из условия самосопряженности  (I.II) следует, что наблюдаемые значения L вещественны.
(I.II) следует, что наблюдаемые значения L вещественны.
Докажем свойство ортогональности собственных функций эрмитовых операторов
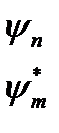


 .
.
Умножим левую и правую части первого равенства на  справа, а для второго равенства проделаем аналогичную операцию, умножив его на
справа, а для второго равенства проделаем аналогичную операцию, умножив его на  ; вычтем получившиеся равенства одно из другого и, проинтегрировав по всему пространству, получим
; вычтем получившиеся равенства одно из другого и, проинтегрировав по всему пространству, получим

Из самосопряженности  (I.II) следует, что левая часть (I.15) равна нулю; следовательно,
(I.II) следует, что левая часть (I.15) равна нулю; следовательно,

 .
.
Формула (I.15) и является условием ортогональности функции 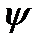 .
.
Если одному L принадлежит несколько 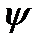 , то состояния, отвечающие этим
, то состояния, отвечающие этим 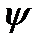 , называют вырожденными.
, называют вырожденными.
Упражнение I.2
Найдите, сколько собственных функций  , определяемых (I.I), соответствуют одному значению импульса
, определяемых (I.I), соответствуют одному значению импульса  . Операторов импульса, согласно формуле (I.10), имеет вид:
. Операторов импульса, согласно формуле (I.10), имеет вид: 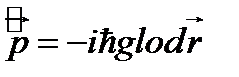 .
.
1.3 Операторы координаты, импульса, момента импульса и энергии
Действие оператора координаты  на функцию
на функцию  сводится к умножению
сводится к умножению  на
на  ; аналогично, действие любой функции координат
; аналогично, действие любой функции координат  сведется к умножению
сведется к умножению 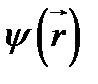 на
на  .
.
Операторы проекции импульса имеют вид
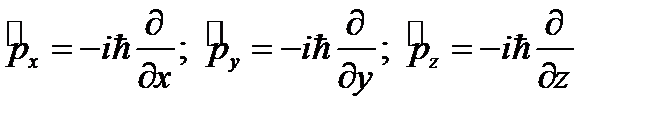
Вычислим коммутатор  операторов
операторов 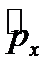 и
и  :
:
 .
.
Таким образом, действие на функцию 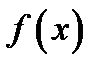 оператора
оператора 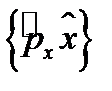 свелось к умножению
свелось к умножению 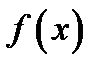 на
на  или говорят, что
или говорят, что

Неравенство нулю коммутатора двух физических величин является аппаратным отражением известным вам из курса общей физики соотношений неопределенности и указывает на невозможность одновременного измерения величин, как в указанном примере координаты  и импульса
и импульса 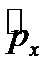 .
.
Момент импульса частицы определялся как векторное произведение

Аналогично из операторов  и
и  строится оператор момента импульса микрочастицы
строится оператор момента импульса микрочастицы
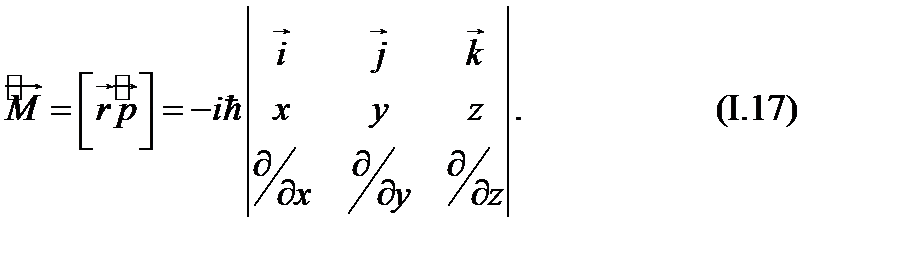
Важное значение имеет оператор квадрата момент импульса микрочастицы 
Значение оператора проекции импульса на координатные оси следуют из (I.17), например,

По операторам проекции  легко записать оператор квадрата момента
легко записать оператор квадрата момента

Упражнение 1.3 
Вычислить коммутатор 
Легко проверить (мы рекомендуем самостоятельно сделать выкладки), что каждая из компонент импульса коммутирует с квадратом полного момента импульса
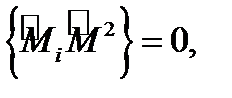 i=x,y,z
i=x,y,z
Как будет установлено на основе решения упражнения 1.3, проекции 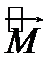 не могут быть измерены одновременно. Но каждая из компонент момента импульса и квадрат момента импульса измеримы одновременно. По этой причине для определения характеристик интересуются, как правило, величинами
не могут быть измерены одновременно. Но каждая из компонент момента импульса и квадрат момента импульса измеримы одновременно. По этой причине для определения характеристик интересуются, как правило, величинами  и
и  .
.
Удобно определить собственные функции и собственные значения  и
и  , перейдя в сферическую систему координат
, перейдя в сферическую систему координат

Здесь 
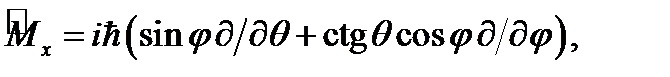


Очевидно, что собственными функциями оператора 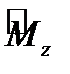 являются экспоненты, где m – целые числа.
являются экспоненты, где m – целые числа.
Собственными функциями  являются сферические функции
являются сферические функции 

где  - целое число,
- целое число,  всего
всего  - значений
- значений  . Поскольку с функциями
. Поскольку с функциями 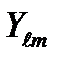 нам достаточно часто придется встречаться в дальнейшем, дадим краткие справочные сведения
нам достаточно часто придется встречаться в дальнейшем, дадим краткие справочные сведения

где 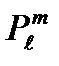 так называемый присоединенный полином Лежандра. Он определяется через полиномы Лежандра
так называемый присоединенный полином Лежандра. Он определяется через полиномы Лежандра 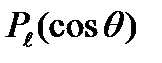 по формуле
по формуле
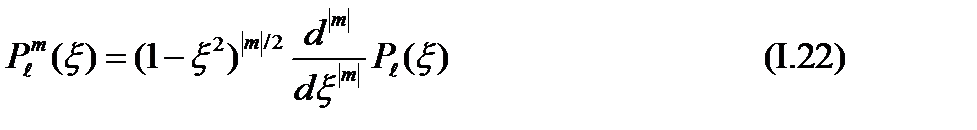
Для полиномов Лежандра существует производящая функция, так что

Однако практического вычисления значительно более удобной оказывается рекуррентная формула

Укажем очень полезную теорему сложения сферических функций

где
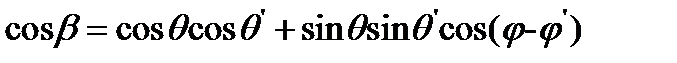
Сферические функции ортогональны

Из (I.18) и (I.19) следуют собственные значения оператора квадрата момента

При этом легко вычисляются собственные значения  в силу экспоненциальной зависимости
в силу экспоненциальной зависимости 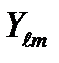 от
от  ;
;
 или
или  .
.
Из (I.26), (I.27) следует, что при заданном значении момента  проекция момента на ось z принимает
проекция момента на ось z принимает  значений. Это наглядно иллюстрируется диаграммой (рис. I.1)
значений. Это наглядно иллюстрируется диаграммой (рис. I.1)

Рис. 1.1
Оператор кинетической энергии частицы 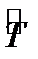 определяется хорошо известной из механики формулой
определяется хорошо известной из механики формулой
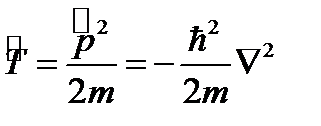
Уравнение для собственных функций

удовлетворяется плоской волной (I.I).
В сферической системе координат оператор  имеет вид
имеет вид

Вспоминая, что  (см.(I.18), (I.19)), получим
(см.(I.18), (I.19)), получим

Оператор полной энергии или гамильтониан 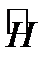 представляет собой сумму операторов кинетической и потенциальной энергии
представляет собой сумму операторов кинетической и потенциальной энергии

Как правило, u(r) является функцией координат, и на нее распространяются те же правила, что и на координату (см. начало настоящего параграфа).
В силу коммутационных соотношений (I.16), кинетическая и потенциальная энергия не могут быть измерены одновременно. В квантовой механике нельзя говорить отдельно о кинетической и потенциальной энергии, полная энергия должна измеряться как единое целое.
Уравнение Шредингера
Так как волновая функция полностью описывает состояние системы, состоящей из одной или нескольких частиц, в данный момент времени, то она же должна определять и эволюцию этой системы.
Это требование выражает принцип причинности в применении к квантовой механике. Пусть нам известно 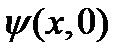 ; тогда
; тогда  можно представить в виде ряда Тейлора, при
можно представить в виде ряда Тейлора, при  можно ограничиться только линейным по
можно ограничиться только линейным по  слагаемым
слагаемым

В силу принципы причинности

 - оператор смещения во времени, причем он должен быть линейным и не должен содержать ни производных, ни интегралов по t.
- оператор смещения во времени, причем он должен быть линейным и не должен содержать ни производных, ни интегралов по t.
Вспомним, что нам известен вид  - функции для случая свободного движения частицы с определенным значением импульса
- функции для случая свободного движения частицы с определенным значением импульса  . Волновая функция такого движения есть плоская волна (I.I).
. Волновая функция такого движения есть плоская волна (I.I).
Дифференцирование (I.I) по t дает
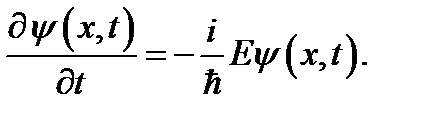
то есть собственным значением этого оператора является полная энергия системы. Следовательно (в чем мы советуем убедиться, проделав непосредственную подстановку), эта волна удовлетворяет уравнению

Делая обобщение этого результата на произвольный случай (см.конец предыдущего параграфа), получаем

Уравнение для волновой функции окончательно запишем в виде

Это уравнение носит название уравнения Шредингера.
Из уравнения Шредингера (УШ) следует закон сохранения числа частиц. Запишем УШ для случая потенциальных сил
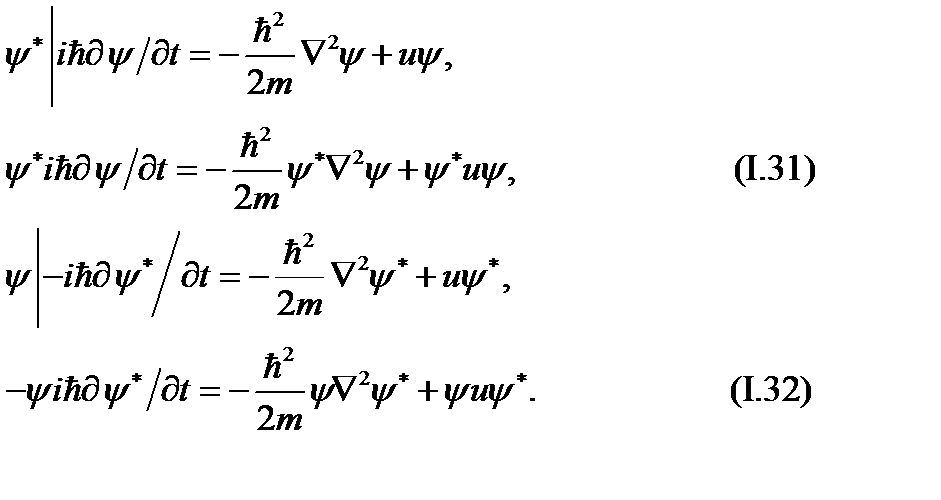
Следом за (1.31) мы написали комплексно-сопряженное уравнение. Умножим, далее, (1.31) на  , (1.32) на
, (1.32) на 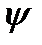 . Сложив затем получившиеся уравнения, получим
. Сложив затем получившиеся уравнения, получим

Если ввести вектор плотности тока вероятности


то (1.33) запишется в форме уравнения непрерывности
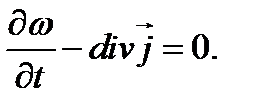

 можно трактовать как плотность числа частиц, а
можно трактовать как плотность числа частиц, а 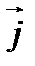 как поток частиц, пересекающих в единицу времени единичную поверхность.
как поток частиц, пересекающих в единицу времени единичную поверхность.
Упражнение 1.4
Интегрируя (1.35) по всему объему и применяя теорему Гаусса, доказать, что полная вероятность найти где-либо в пространстве частицу не зависит от времени.
Упражнение 1.5
Доказать закон сохранения заряда.
У.Ш. имеет важные решения, получающиеся методом разделения переменных. Пусть
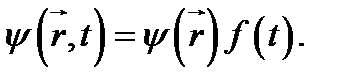 (1.36)
(1.36)
Подставляя (1.36) в У.Ш. (1.30), получаем

или
 (1.37)
(1.37)
где E – не зависящая ни от t, ни от  константа разделения. С другой стороны, из последнего равенства (1.37) следует, что E представляет собой собственные значения оператора полной энергии
константа разделения. С другой стороны, из последнего равенства (1.37) следует, что E представляет собой собственные значения оператора полной энергии  (оператора Гамильтона). Зависимость от времени определяется тривиально
(оператора Гамильтона). Зависимость от времени определяется тривиально
 (1.38)
(1.38)
Найдем в качестве упражнения вероятность местонахождения частицы с волновой функцией (1.38) в данном объеме 

или

т.е. вероятность нахождения частицы в объеме  , волновая функция которой (
, волновая функция которой ( стационарное состояние) не зависит от времени.
стационарное состояние) не зависит от времени.
Упражнение 1.6
Воспользовавшись (1.34), (1.38), докажите, что плотность тока в n -м стационарном состоянии не зависит от времени.
1.5 Прохождение частиц и отражение их от потенциальных барьеров
В этом параграфе мы ответим на первый и третий вопросы, поставленные вначале главы. Здесь будет рассмотрен случай движения частицы в той области, где потенциальная энергия U>E больше полной энергии. Такие области недоступны для классических частиц, движение которых подчиняется законам Ньютона.
Изучим движение частицы в том случае, когда потенциальная функция (i) одномерна и (ii) описывается ступенькой (рис.1.2)

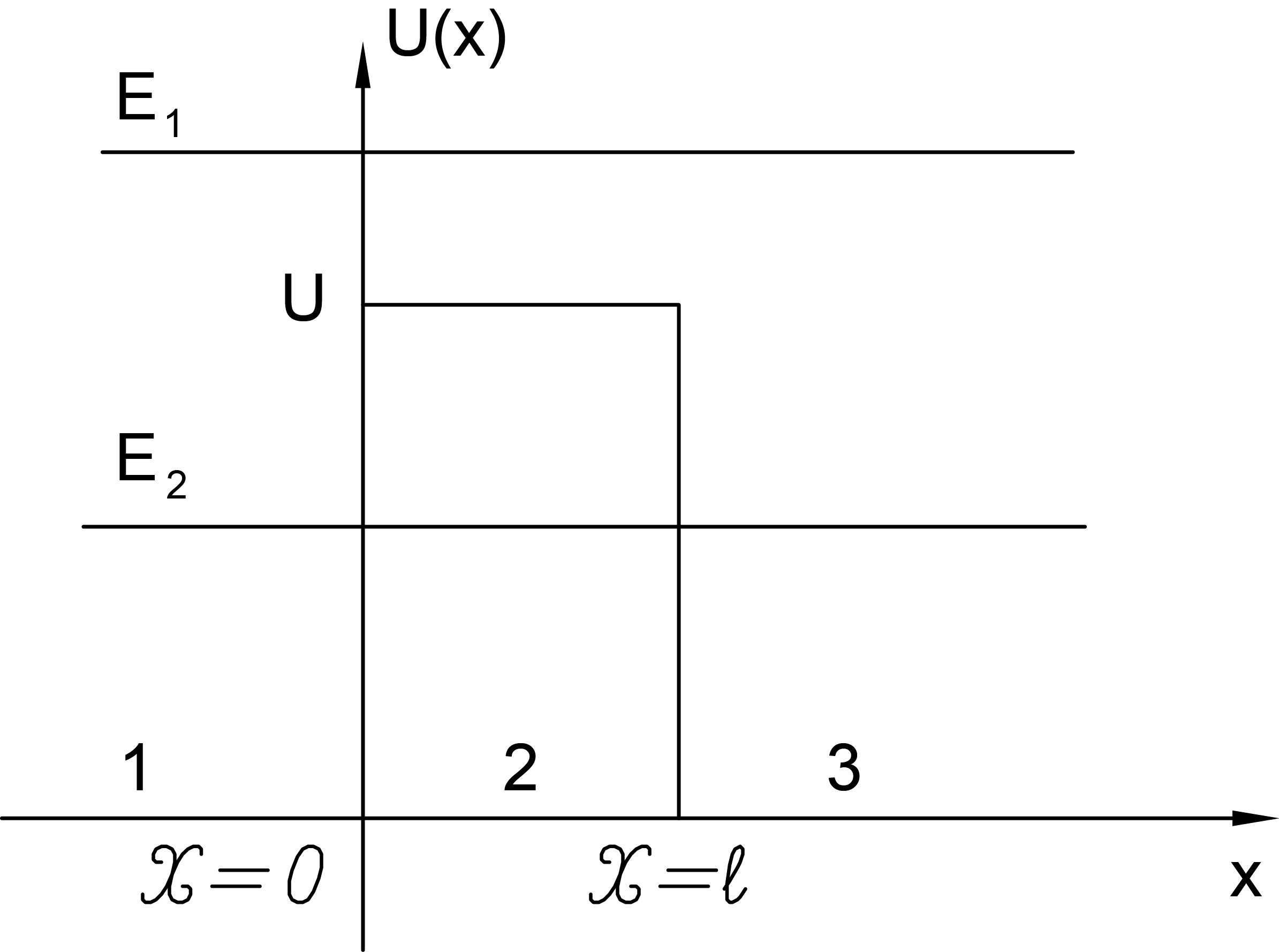
Рис. 1.2

Движение частицы будем описывать стационарным У.Ш.
 (1.39)
(1.39)
в одномерном случае 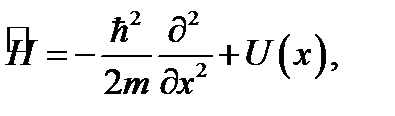
и У.Ш. (1.39) превращается в дифференциальное уравнение
 (1.40)
(1.40)
Общее решение уравнения (1.40) находится по обычным правилам

где  - корни характеристического уравнения
- корни характеристического уравнения
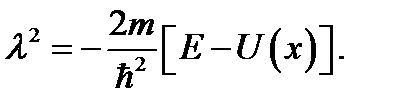 Таким образом,
Таким образом,

Решение для трех характерных областей потенциальной энергии принимают вид
 (1.41а)
(1.41а)
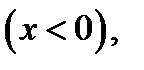
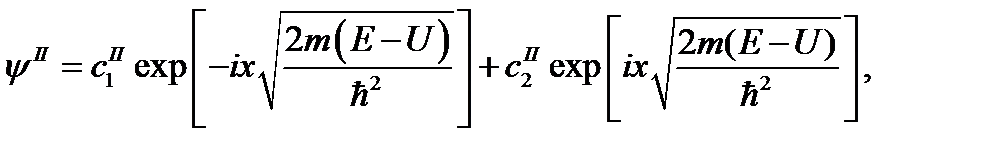 (1.41б)
(1.41б)

 (1.41в)
(1.41в)

Сейчас мы должны проделать процедуру, которую обычно называют сшивкой решений и которая приведет к нахождению одной функции 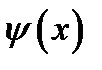 , описывающей состояние частицы, движущейся в силовом поле.
, описывающей состояние частицы, движущейся в силовом поле.
Для этого необходимо установить граничные условия. Первое – следует из требования непрерывности волновой функции
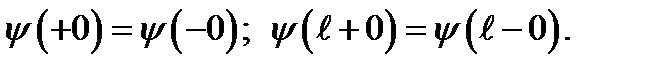 (1.42)
(1.42)
Проинтегрируем уравнение (1.40) в окрестности точки x = 0


переходя к пределу  получаем
получаем

аналогично получаем
 (1.43)
(1.43)
Условие (1.43) отражает требование непрерывности плотности тока (см.(1.34)).
Подставляя в (1.42) и (1.43) значения функций (1.41), получаем систему из 4 уравнений
 (1.44а)
(1.44а)
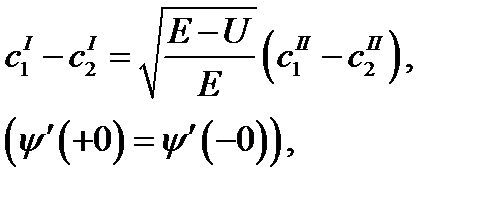 (1.44б)
(1.44б)
 (1.44в)
(1.44в)
 (1.44г)
(1.44г)
Система из четырех уравнений (1.44) определяет шесть неизвестных констант. Недостающие параметры определяются начальными условиями.
Пусть  - это соответствует случаю падающей слева волны. Примем, не ограничивая общности, амплитуду падающей волны равной единице
- это соответствует случаю падающей слева волны. Примем, не ограничивая общности, амплитуду падающей волны равной единице  . Тогда система уравнений (1.44) трансформируется к виду
. Тогда система уравнений (1.44) трансформируется к виду
 (1.45)
(1.45)


Решение системы линейных уравнений (1.45) без труда находится. Оно имеет довольно громоздкий вид
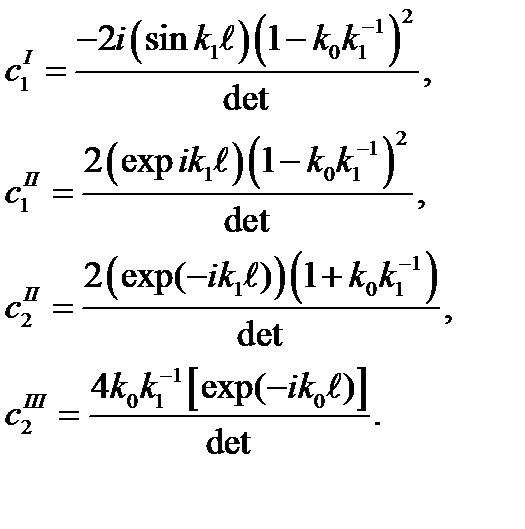 (1.46)
(1.46)
где
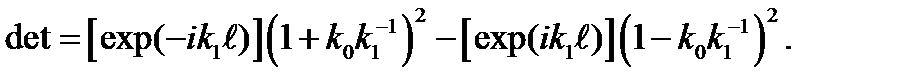
Величина  , определяема отношением волновых чисел частиц в 1,2-й областях значений потенциала, имеет хорошо известный в оптике аналог – показатель преломления среды. Если энергия E частицы больше высоты барьера U, то, как это следует из (1.45), n – действительная величина (в дальнейшем
, определяема отношением волновых чисел частиц в 1,2-й областях значений потенциала, имеет хорошо известный в оптике аналог – показатель преломления среды. Если энергия E частицы больше высоты барьера U, то, как это следует из (1.45), n – действительная величина (в дальнейшем  = n). Отраженная от барьера волна определяется отрицательным значением
= n). Отраженная от барьера волна определяется отрицательным значением 

ее интенсивность определяется квадратом амплитуды 
 (1.47)
(1.47)
Аналогично интенсивность волн, прошедший барьер, определится квадратом 
 (1.48)
(1.48)
Вычислим плотность тока (формула (1.34)) в падающей волне  , отраженной
, отраженной 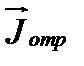 и проходящей
и проходящей  . Советуем вам проделать эти выкладки самостоятельно. Результаты вычислений по (1.34) дадут
. Советуем вам проделать эти выкладки самостоятельно. Результаты вычислений по (1.34) дадут
 (1.49)
(1.49)
(Заметим, что  - скорость волны в данной области.)
- скорость волны в данной области.)
Отношение потока отраженных частиц к потоку падающих носит название коэффициента отражения R
 (1.50)
(1.50)
Отношение потока прошедших частиц к потоку падающих называют прозрачностью барьера T
 (1.51)
(1.51)
Из закона сохранения числа частиц (уравнение непрерывности (1.35)) следует, что
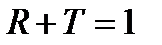 .
.
В классическом случае, когда движение подчиняется законам Ньютона, при  , т.е. барьер прозрачен, наличие его приведет лишь к уменьшению скорости движения частицы во II-ой области. Микрочастицы, движение которых подчиняется У.Ш., частично отражаются
, т.е. барьер прозрачен, наличие его приведет лишь к уменьшению скорости движения частицы во II-ой области. Микрочастицы, движение которых подчиняется У.Ш., частично отражаются  (см.(1.50)), частично проходят через барьер T<1 (см.(1.51)). Таким образом, здесь реализуется известная в оптике ситуация отражения света от границы раздела сред с разными показателями преломления.
(см.(1.50)), частично проходят через барьер T<1 (см.(1.51)). Таким образом, здесь реализуется известная в оптике ситуация отражения света от границы раздела сред с разными показателями преломления.
В случае E<U из классических законов следует: Т=0, R=1 (в оптике это соответствует полному внутреннему отражению). Рассмотрим, что следует из уравнения (1.47) - (1.51) в квантовомеханическом случае

 (1.52)
(1.52)
и, подставляя (1.49) в (1.51), с учетом (1.52), получим
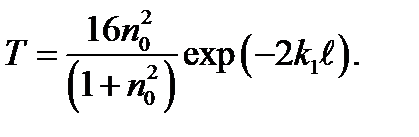
Более принята в литературе несколько иная запись коэффициента прозрачности
 (1.53)
(1.53)
где 
Это квантовомеханическое явление прохождения частиц через потенциальный барьер получило название туннельного эффекта.
Упражнение 1.7
Туннельный эффект будет иметь заметное значение, если
 (1.54)
(1.54)
Оценить чему должно равняться в случае электрона  (если
(если 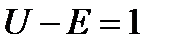 электрон-вольт), чтобы выполнить соотношение (1.45).
электрон-вольт), чтобы выполнить соотношение (1.45).
Рассмотрим прохождение частиц через барьер с помощью приближенного метода, который носит название квазиклассического приближения.
Заменим непрерывный потенциал рядом ступенчатых барьеров (рис.1.3).

Рис. 1.3
В каждой области dx реальный потенциал заменится на постоянный. Пусть коэффициент пропускания i – го прямоугольника равен  . В силу определения (1.51) поток, подошедший ко второй ступеньке, будет иметь значение
. В силу определения (1.51) поток, подошедший ко второй ступеньке, будет иметь значение

Аналогично
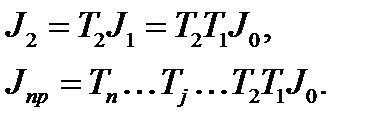 (1.55)
(1.55)
Подставляя (1.53) в (1.55), получим

Переходя к бесконечному пределу и заменяя сумму интегралом, получаем
 (1.56)
(1.56)
Точки 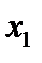 и
и  в классических задачах носят название точек поворота.
в классических задачах носят название точек поворота.
Изложенная в данном параграфе теория позволяет описать очень широкий круг явлений. Расскажем в следующем параграфе о двух из них:  - распаде и автоионизации.
- распаде и автоионизации.
1.6  - распад, автоионизация
- распад, автоионизация
Все атомные системы, могущие пребывать в стационарных состояниях (атом, ядро, молекула, кристалл), представляют собой набор частиц, каждая из которых находится в потенциальной яме.
Распад радиоактивных элементов сопровождается испусканием 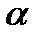 - частиц. Представим себе
- частиц. Представим себе  - частицу как самостоятельный объект, имеющий двукратный положительный заряд. Вдали от ядра потенциал определяется кулоновским отталкиванием:
- частицу как самостоятельный объект, имеющий двукратный положительный заряд. Вдали от ядра потенциал определяется кулоновским отталкиванием: 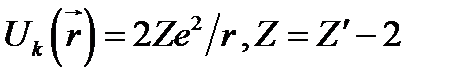 , где
, где  - заряд исходного ядра. Вблизи ядра на малых расстояниях действуют неэлектростатические силы притяжения (на их природе мы останавливаться не будем) так, что график потенциальной энергии
- заряд исходного ядра. Вблизи ядра на малых расстояниях действуют неэлектростатические силы притяжения (на их природе мы останавливаться не будем) так, что график потенциальной энергии  - частицы имеет вид, представленный на рис. 1.4:
- частицы имеет вид, представленный на рис. 1.4:
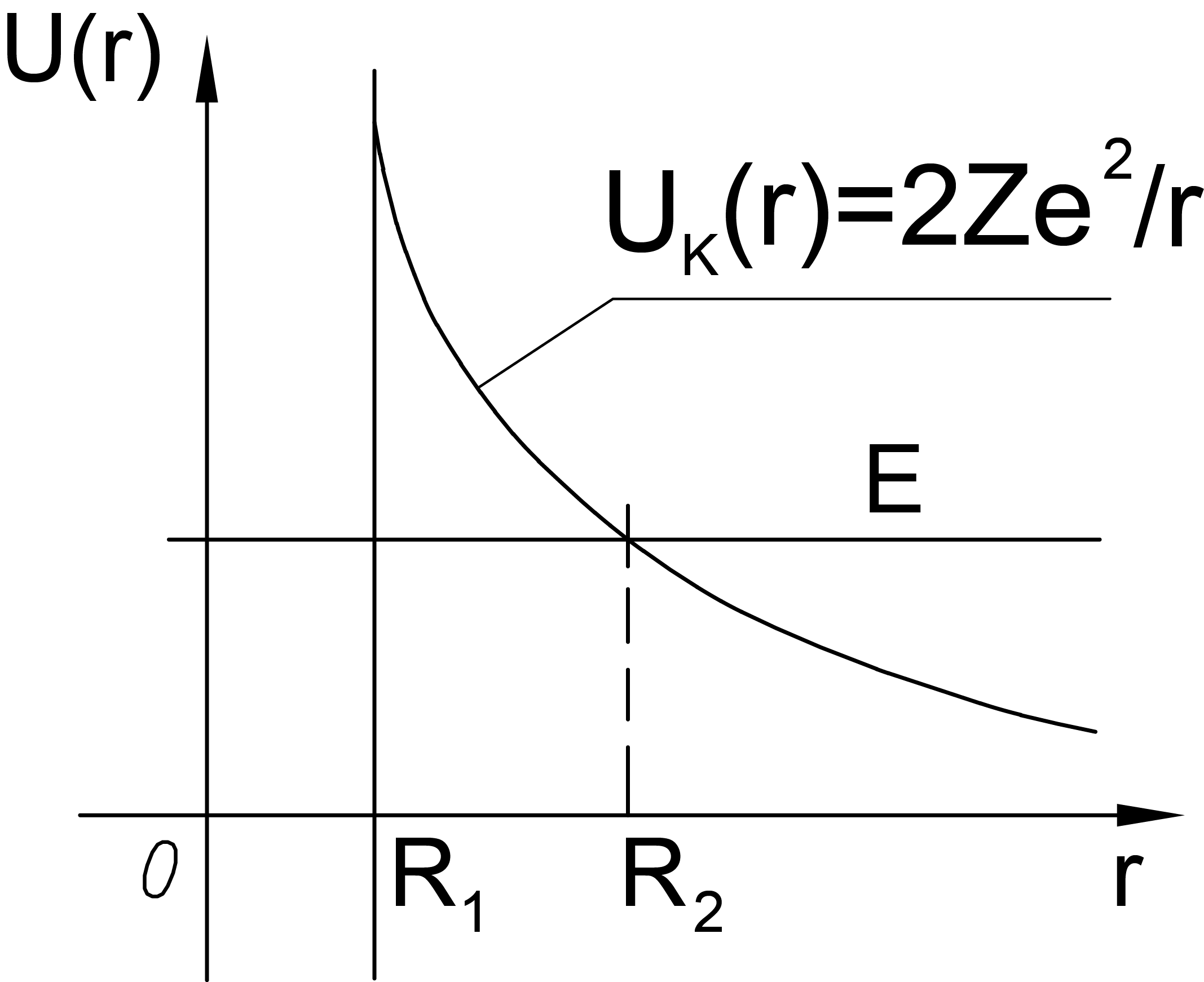
Рис. 1.4
Из представленной на рис. 1.4 схеме следует, что  - частица покидает ядро, туннелируя через барьер в области
- частица покидает ядро, туннелируя через барьер в области  до
до  .
.
Коэффициент пропускания для представленного на рис. 1.3 барьера вычислим с помощью формулы (1.56). Подынтегральное выражение в (1.56) имеет резкий максимум при  . Это вызвано тем, что мы приближенно внутреннюю стенку потенциального барьера сделали вертикальной. Чтобы взять интеграл, поступают следующим образом:
. Это вызвано тем, что мы приближенно внутреннюю стенку потенциального барьера сделали вертикальной. Чтобы взять интеграл, поступают следующим образом:
1) вводят новую переменную 

2) поскольку  , разбивают
, разбивают

Из рис.1.4 следует 
Окончательно
 (1.57)
(1.57)
Рассмотрим явление ионизации атомов в сильных электрических полях.
Потенциальная энергия электрона в атоме в отсутствие внешнего поля имеет известную зависимость  , например, для атома водорода
, например, для атома водорода  . Тогда, в однородном электрическом поле напряженностью
. Тогда, в однородном электрическом поле напряженностью  потенциальная энергия электрона будет равна
потенциальная энергия электрона будет равна
 (1.58)
(1.58)
Рассмотрим график потенциальной энергии в плоскости  , рис.1.5.
, рис.1.5.
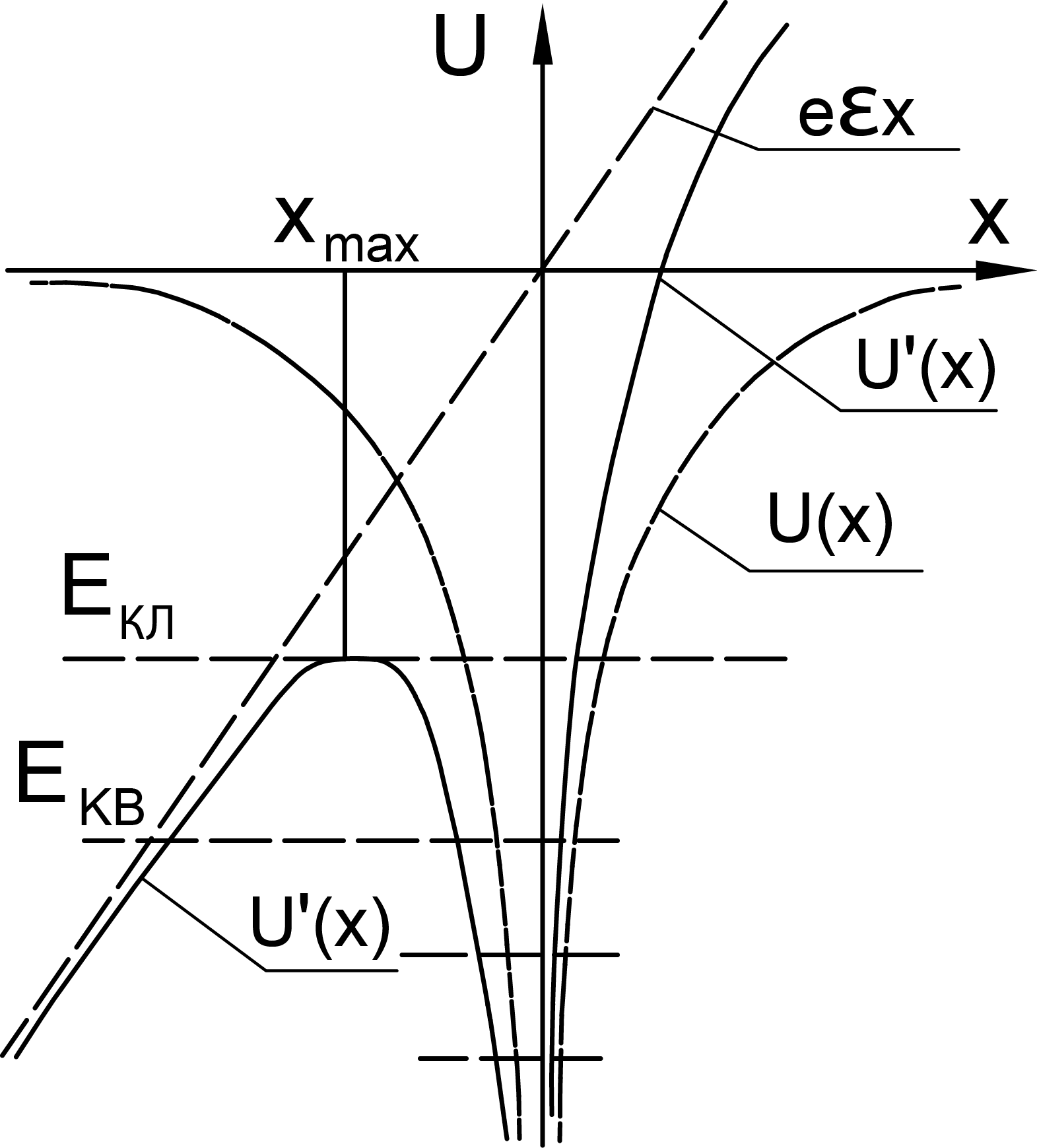
Рис. 1.5
Появление электрического поля приводят к образованию барьера в области, обозначенной на рисунке  . Для электронов с энергией
. Для электронов с энергией  открывается возможность покинуть атом в согласии с законами классической механики. При
открывается возможность покинуть атом в согласии с законами классической механики. При  открывается канал ухода электронов квантовомеханическим туннелированием. Поэтому и классическая механика приводит к возможности ионизации атома электрическим полям.
открывается канал ухода электронов квантовомеханическим туннелированием. Поэтому и классическая механика приводит к возможности ионизации атома электрическим полям.
Однако по законам квантовой механики ионизация не носит резкого, порогового характера, что находится в соответствии с экспериментальными данными.
1.7 Водородоподобные системы. Рентгеновские термы атомов. Статистическая модель атома.
Рассмотрим систему, состоящую из ядра с зарядом  и движущегося вокруг него электрона. Полная энергия электрона в системе координат, связанной с покоящимся ядром, равно
и движущегося вокруг него электрона. Полная энергия электрона в системе координат, связанной с покоящимся ядром, равно  Таким образом, уравнение Шредингера имеет вид
Таким образом, уравнение Шредингера имеет вид
 (1.59)
(1.59)
В сферической системе координат придем к записи (1.59) в виде
 (1.59а)
(1.59а)
Решение уравнения (1.59) будем искать в виде
 (1.60)
(1.60)
где  - радиальная, а
- радиальная, а  - уже знакомая
- уже знакомая