Свойство 1. Производная от неопределённого интеграла равна подынтегральной функции, то есть если 
, то
Свойство 2. Дифференциал от неопределённого интеграла равен подынтегральному выражению
Свойство 3. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы
Свойство 4. Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов
Свойство 5. Неопределённый интеграл от разности функций равен соответствующей разности неопределённых интегралов
Свойство 6. Постоянный множитель можно выносить за знак интеграла
Свойство 7. Если
,то
Вопрос 16.Таблица неопределенных интегралов.
1) 
2) 
3) 
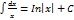
4) 
5) 
6) 
7) 
8) 
9) 
10) 
11) 
Вопрос 17. Методы интегрирования: непосредственное интегрирование
Непосредственное интегрирование
Непосредственное интегрирование основано на свойстве 4 неопределенного интеграла Если функции f1(x), … fn(x) имеют первообразные в некотором промежутке, то функция f(x) = f1(x)+f2(x)+f3(x)+…+-fn(x) также имеет первообразную в том же промежутке, причем
т.е. неопределенный интеграл от суммы некоторого числа функций равен такой же сумме неопределенных интегралов от слагаемых.
Вопрос 18. Методы интегрирования: замена переменной.
Метод подстановки
Интегрирование производимое введением новой переменной (или метод подстановки) основано на формуле
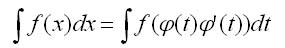
где x = ф(t) — дифференцируемая функция переменой t.
Вопрос 19. Методы интегрирования: формула интегрирования по частям.
Метод интегрирования по частям
Если u = u (х), v = v (х) - дифференцируемые функции от х, то из формулы для дифференциала произведения двух функций d(uv) = udv+vdu получается формула интегрирования по частям
Эта формула применяется в случае, когда подынтегральная функция представляет собой произведение алгебраической и трансцендентной функций. В качестве и обычно выбирается функция, которая упрощается дифференцированием, в качестве dv — оставшаяся часть подынтегрального выражения, содержащая dx, из которой можно определить v путем интегрирования.
Для сведения данного интеграла к одной из формул простейших интегралов формулу нужно применить несколько раз. Иногда искомый интеграл определяется из алгебраического уравнения, получающегося с помощью интегрирования по частям.
Вопрос 20.Определенный интеграл, его геометрический смысл и свойства. Формула Ньютона – Лейбница.
Геометрический смысл. Самая популярная задача – вычисление площади с помощью определенного интеграла.
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.
Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница:
Формула Ньютона
|
непрерывна на отрезке 
и 
— ее любая первообразная на этом отрезке, то имеет место равенство
21.Дифференциальные уравнения 1-го порядка. Общее и частное решения. Задача и теорема Коши.
Дифференциальное уравнение первого порядка, содержит:
1) независимую переменную;
2) зависимую переменную (функцию);
3) первую производную функции:.
В некоторых случаях в уравнении первого порядка может отсутствовать «икс» или (и) «игрек» – важно чтобы в ДУ была первая производная, и не было производных высших порядков –, и т.д.
Решить дифференциальное уравнение – это значит, найти множество функций, которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.
22.Определение и способы решения Дифференциальных уравнений с разделяющимися переменными, однородных и линейных дифференциальных уравнений 1-го порядка.
Дифференциальное уравнение - это уравнение, в котором неизвестной величиной является некоторая функция.При этом, в самом уравнении участвует не только неизвестная функция, но и различные ее производные. Дифференциальным уравнением описывается связь между неизвестной функцией и ее производными. Такие связи отыскиваются в различных областях знаний: в механике, физике, химии, биологии, экономике и др.
Различают обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных. Более сложными являются интегро-дифференциальные уравнения.
Сначала дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции от времени.
Дифференциальное уравнение называется интегрируемых в квадратурах, если задачу нахождения всех развязок связей
можно свести к вычислению конечного числа интегралов от известных функций и п
gростых алгебраических операций.
23.Понятие множеств и способы их задания
Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть не сводимое к другим понятиям, а значит и не имеющее определения. Однако, существуют различные описания множества..
Существуют два основных способа задания множеств: перечисление и описание его элементов. Перечисление состоит в получении полного списка элементов множества, а описание заключается в задании такого свойства, которым элементы данного множества обладают, а все остальные нет.
Конечные множества можно задавать обоими способами, причем выбор того или иного способа зависит от удобства задания и дальнейшей работы с множеством. Бесконечные множества можно задавать только с помощью описания.
24.Операции над множествами. Диаграммы Эйлера-Венна.
Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.
Операции над множествами рассматриваются для получения новых множеств из уже существующих
25.События и их квалификация. Классическое определение вероятности и случайного события.
Теория вероятностей – математическая наука, которая по вероятностям одних событий позволяет оценивать вероятности других событий, связанных с первыми.
Подтверждением того, что понятие «вероятность события» не имеет определения, является тот факт, что в теории вероятностей существует несколько подходов к объяснению этого понятия:
Классическое определение вероятности случайного события.
Вероятность события равна отношению числа благоприятных событию исходов опыта к общему числу исходов опыта
Исход опыта называется благоприятным для события, если при этом исходе опыта появилось событие. Например, если событие - появление карты красной масти, то появление туза бубей – исход, благоприятный событию.
Примеры.
1) Вероятность выпадения 5 очков на грани кубика равна, поскольку кубик может упасть любой из 6 граней кверху, а 5 очков находятся только на одной грани.
2) Вероятность выпадения герба при однократном бросании монеты -, поскольку монета может упасть гербом или решкой – два исхода опыта, а герб изображен лишь на одной стороне монеты.
3) Если в урне 12 шаров, из которых 5 – черные, то вероятность вынуть черный шар -, поскольку всего исходов опята – 12, а благоприятных из них - 5
Замечание. Классическое определение вероятности применимо при двух условиях:
1) все исходы опыта должны быть равновероятными;
2) опыт должен иметь конечное число исходов.
26.Комбинаторика. Общие правила комбинаторики (применить на примерах).
Комбинато́рика— раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). C точки зреня теории множеств комбинаторика изучает подмножества конечных множеств, их объединения и пересечения, а так же различные способы упорядочивания этих подмножеств. Основными и типичными операциями и связанными с ними задачами комбинаторики
являются следующие:
1) образование упорядоченных множеств, состоящее в установлении определенного
порядка следования элементов множества друг за другом, - составление
перестановок;
2) образование подмножеств, состоящее в выделении из данного множества
некоторой части его элементов, - составление сочетаний;
3) образование упорядоченных подмножеств - составление размещений.
27.Определение размещений и формула для их вычислений, привести пример.