Метод вариации произвольных постоянных для построения решения линейного неоднородного дифференциального уравнения

Характеристическое уравнение имеет два различных действительных корня

Если характеристическое уравнение имеет два различных действительных корня , (т.е., если дискриминант ), то общее решение однородного уравнения выглядит так:
, где – константы.

В случае если один из корней равен нулю, решение очевидным образом упрощается; пусть, например, , тогда общее решение:

22. Два равных корня

Характеристическое уравнение имеет два кратных действительных корня

Если характеристическое уравнение 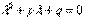имеет два кратных (совпавших) действительных корня 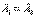(дискриминант ), то общее решение однородного уравнения принимает вид:
, где – константы.
Вместо в формуле можно было нарисовать , корни всё равно одинаковы.

Если оба корня равны нулю 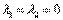, то общее решение опять же упрощается: . Кстати, является общим решением того самого примитивного уравнения , о котором я упоминал в начале урока. Почему? Составим характеристическое уравнение: – действительно, данное уравнение как раз и имеет совпавшие нулевые корни .

23. Комплексные корни

Характеристическое уравнение имеет сопряженные комплексные корни

Если характеристическое уравнение имеет сопряженные комплексные корня 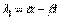, (дискриминант ), то общее решение однородного уравнения принимает вид:
, где – константы.
Примечание: Сопряженные комплексные корни почти всегда записывают кратко следующим образом:

Если получаются чисто мнимые сопряженные комплексные корни: , то общее решение упрощается:

Пример 5

Решить однородное дифференциальное уравнение второго порядка

Решение: Составим и решим характеристическое уравнение:


– получены сопряженные комплексные корни

Ответ: общее решение:

24. Неоднородные уравнения

Неоднородное уравнение интегрируется методом вариации произвольных постоянных (Метод Лагранжа). Вид общего решения неоднородного уравнения.Если дано частное решение неоднородного уравнения , и — фундаментальная система решений соответствующего однородного уравнения, то общее решение уравнения задается формулой

где — произвольные постоянные.

Принцип суперпозиции

В случае, когда функция в правой части состоит из суммы двух функций

,

частное решение неоднородного уравнения тоже состоит из суммы двух функций

,

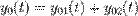где являются решениями неоднородного уравнения с правыми частями 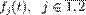, соответственно.

Рассмотрим линейное неоднородное дифференциальное уравнение

y ^{( n )} + a_{n -1}(x) y ^{( n - 1)} +... + a ₁(x) y ' + a ₀(x) y = f (x).

Общим решением этого уравнения на отрезке [ a; b ] называется функция y = Φ(x, C ₁,..., C_n), зависящая от n произвольных постоянных C ₁,..., C_n и удовлетворяющая следующим условиям:

− при любых допустимых значениях постоянных C ₁,..., C_n функция y = Φ(x, C ₁,..., C_n) является решением уравнения на [ a; b ];

− какова бы ни была начальная

точка (x ₀, y ₀, y _1,0,..., y_{n − 1,0}), x ₀∈ [ a; b ], существуют такие значения C ₁ = C ₁₀,..., C_n = C_{n 0}, что функция y = Φ(x, C ₁₀,..., C_{n 0}) удовлетворяет начальным условиям y (x ₀) = y ₀, y '(x ₀) = y _1,0,..., y ^{(n − 1)} (x ₀) = y_{n − 1,0}.

Справедливо следующее утверждение (теорема о структуре общего решения линейного неоднородного уравнения).

Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b], а функции y₁(x), y₂(x),..., y _n (x) образуют фундаментальную систему решений соответствующего однородного уравнения, то общее решение неоднородного уравнения имеет вид

y(x,C₁,..., C _n) = C₁ y₁(x) + C₂ y₂(x) +... + C _n y_n (x) + y *(x),

где C₁,...,C _n — произвольные постоянные, y *(x) — частное решение неоднородного уравнения.

25. Метод вариации произвольных постоянных

Метод Лагранжа (метод вариации произвольных постоянных) — метод для получения общего решения неоднородного уравнения, зная общее решение однородного уравнения без нахождения частного решения.

Метод вариации произвольных постоянных для построения решения линейного неоднородного дифференциального уравнения

Метод состоит в замене произвольных постоянных 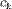в общем решении

соответствующего однородного уравнения

на вспомогательные функции , производные которых удовлетворяют линейной алгебраической системе

Определителем системы (1) служит вронскиан функций , что обеспечивает её однозначную разрешимость относительно .

Если — первообразные для , взятые при фиксированных значениях постоянных интегрирования, то функция

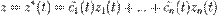
является решением исходного линейного неоднородного дифференциального уравнения. Интегрирование неоднородного уравнения при наличии общего решения соответствующего однородного уравнения сводится, таким образом, к квадратурам.