Алгебраическая форма комплексных чисел

Пусть x и y – обычные числа. Число вида

z = x + iy

называется комплексным числом в алгебраической форме.

x называют вещественной или действительной частью числа z и обозначают так: ; y называют мнимой частью числа z и обозначают так: . Число называют комплексно сопряженным числу z. Действует следующее общее правило: «чтобы получить число, комплексно сопряженное данному, надо в нем заменить i на – i ».

Рассмотрим операции над комплексными числами в алгебраической форме. Пусть даны два комплексных числа и .

17)Показательная и тригонометрические функции в области комплексных чисел связаны между собой формулой

(17.10)

которая носит название формулы Эйлера. Обосновать ее можно с помощью теории степенных рядов. Эта теория будет изложена в курсе математического анализа.

Пусть комплексное число в тригонометрической форме имеет вид 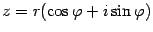. На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим

Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь , .

Пусть . Положим , . Из рисунка 17.4 очевидно, что

Тогда . Это выражение запишем в виде

(17.8)

Последняя запись называется тригонометрической формой комплексного числа. В отличие от нее запись числа в виде 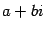называют иногда алгебраической формой комплексного числа.

Отметим, что тригонометрическая форма -- это указание числа по двум его характеристикам: модулю и аргументу. Поэтому вместо формулы (17.8) можно было бы просто записывать пару , но запись (17.8) принята в силу традиции.

18)Сравнение

означает, что и (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

· Сложение

· Вычитание

· Умножение

· Деление

· В частности,

19)На каждой прямой и в каждой плоскости имеются по крайней мере две точки.

· В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии.

· Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.

· Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

· Если две точки прямой лежат на одной плоскости, то все точки данной прямой лежат в этой плоскости.

· Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

· Любая плоскость α разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что:

1. любые две точки, принадлежащие разным множествам, разделены плоскостью α;

2. любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью α.

· Расстояние между любыми двумя точками пространства одно и то же на любой плоскости, содержащей эти точки.

20) Теорема 15.1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.

22)Теорема 15.3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

23) Теорема 16.1. Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну.

27)Теорема 16.5. Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.

28)1°. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.2°. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

29)Теорема 17.1. Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны.

34)Теорема 17.6.Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

35)Расстояние между скрещивающимися прямыми]

Пусть прямые заданы векторными параметрическими уравнениями:

Тогда расстояние между ними можно определить, используя операции смешанное произведение и векторное произведение: