Характеристическое уравнение.

Если имеется однородное линейное дифференциальное уравнение c постоянными коэффициентами

р ₀ у ⁽ⁿ⁾ + p ₁ y ^{(n -1)} + … + p_ny = 0, то алгебраическое уравнение

p ₀λ ⁿ + p ₁λ ^{n -1} + … + p_n = 0 называется его характеристическим уравнением.

 

22# Линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка с постоянными коэффициентами — это уравнения вида

Общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами можно записать как сумму

где y_o- это общее решение линейного однородного уравнения с постоянными коэффициентами

Y- частное решение ЛНДУ.

В некоторых специальных случаях частное решение ЛНДУ может быть найдено методом неопределенных коэффициентов, в общем случае используют метод вариации произвольных постоянных. В данном пункте мы рассмотрим неоднородные дифференциальные уравнения с правой частью специального вида и применим метод неопределенных коэффициентов, а метод вариации произвольных постоянных будет изложен позже.

Общее решение неоднородного дифференциального уравнения второго порядка ищем в зависимости от вида правой части, то есть от функции f(x).

где — многочлен степени n.

Ia. Если a не является корнем характеристического уравнения, то есть то частное решение ЛНДУ ищем в виде

где — многочлен степени n с постоянными коэффициентами.

Iб. Если a — один из корней характеристического уравнения, то если верно только одно из равенств то частное решение ЛНДУ ищем в виде

Iв. Если a — кратный корень характеристического уравнения, то есть (например, при дискриминанте, равном 0), то частное решение неоднородного дифференциального уравнения второго порядка в этом случае есть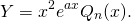

IIa. Если a+bi не является корнем характеристического уравнения, то есть то частное решение неоднородного дифференциального уравнения ищем как

Где многочлены степени N, N — больная из степеней n и m.

IIб. Если a+bi является корнем характеристического уравнения, то есть то для этого случая частное решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами ищем в виде

Метод неопределённых коэффициентов ― метод, используемый в математике для нахождения искомой функции в виде точной или приближённой линейной комбинации конечного или бесконечного набора базовых функций. Указанная линейная комбинация берётся с неизвестными коэффициентами, которые определяются тем или иным способом из условий рассматриваемой задачи. Обычно для них получается система алгебраических уравнений.

Применение метода неопределённых коэффициентов основано на следующих двух теоремах.

Теорема №1 (о многочлене, тождественно равном нулю).

Если при произвольных значениях аргумента x значение многочлена f(x) = а ₀+ а ₁ х + а ₂ х ² +...+ а _n x ⁿ, заданного в стандартном виде, равно нулю, то все его коэффициенты а₀, а₁, а₂,..., а_n равны нулю.

Теорема №2 (следствие теоремы № 1).

Пусть и f(x) = а ₀+ а ₁ х +...+ а _n x ⁿ, и g (x) = b ₀+ b ₁х + b ₂ х ² +...+ b _n x ⁿ.
Для того чтобы f(x)= g(x) необходимо и достаточно, что бы а ₀= b ₀, а ₁ = b ₁, а ₂ = b ₂,..., а _n= b _n
Рассмотрим примеры, иллюстрирующие использование метода неопределенных коэффициентов.

 

23#Пусть задана бесконечная числовая последовательность u₁, u₂,…,u_n,…. Выражение (1) называется числовым рядом. Числа u₁, u₂,…,u_n,… называются первым, вторым, …, n- м, … членами ряда. u_n также называется общим членом ряда. Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда: Если существует конечный предел то он называется суммой ряда (1), а ряд (1) называется сходящимся. Если не существует или равен бесконечности, то ряд (1) называется расходящимся и суммы не имеет.

 

24# Необходимый признак сходимости.

Если ряд сходится, то u_n= 0.

Доказательство. Пусть ряд u₁+u₂+…+u_n… сходится, то есть существует конечный предел 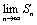= S. Тогда имеет место также равенство = S, так как при n и (n-1) . Вычитая почленно (ха-ха, член) из первого равенства второе, получаем - = = u_n =0, что и требовалось доказать.

Следствие. Если u_n ≠0, то ряд u₁+u₂+…+u_n… расходится.

Признак сравнения

Пусть даны два знакоположительных числовых ряда

(7)

(8)

причём u_n≤v_n при любых n =1,2,….

Тогда: 1. Если ряд (8) сходится, то сходится и ряд (7);

2. Если ряд (7) расходится, то расходится и ряд (8).

Доказательство. Обозначим n -е частичные суммы рядов (7) и (8) через S_n и s_n соответственно. Пусть ряд (8) сходится. Это значит, что существует конечный =s. По условию теоремы 0< u_n ≤ v_n, поэтому S_n < s_n < s при всех n =1,2,…, то есть последовательность { S_n } ограничена, следовательно, ряд (7) сходится. Пусть теперь ряд (7) расходится, то есть = ∞. Тогда из неравенства S_n < s_n следует, что и = ∞, следовательно, ряд (8) расходится. Теорема доказана.

Признак Даламбера

Пусть дан знакоположительный числовой ряд

(7)

и пусть существует предел При p <1 ряд (7) сходится, при p >1 ряд (7) расходится.

Доказательство. По условию существует предел 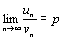. Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n³N выполняется условие или

p-E< (10)

Пусть сначала p <1. Выберем Е так, что p+E=q<1. Для всех n³N имеем … или

или

(11)

Рассмотрим ряды

(12)

. (13)

Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.

Пусть теперь p >1. Выберем Е так, что p-E >1. Тогда из левой части неравенства (10) следует, что при n³N выполняется или u_n+1>u_n, то есть члены ряда возрастают с возрастанием номера n. Поэтому u_n ¹0, следовательно, ряд расходится по следствию из необходимого признака сходимости. Теорема доказана.

 

25# Радикальный признак Коши

Пусть дан знакоположительный числовой ряд u₁+u₂+…+u_n… (7)

и пусть существует предел При p <1 ряд (7) сходится, при p >1 ряд (7) расходится.

Доказательство. По условию существует Это означает, что для любого положительного числа Е существует такой номер N, что для всех n³N выполняется условие | | < E или p-E< <p+E. (14)

Пусть p <1. Выберем Е таким, чтобы выполнялось p+E=q<1. Тогда из (14) получаем < q или u_n < qⁿ для всех n³N. Рассмотрим ряды

(15)

(16)

Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что u_n < qⁿ для всех n³N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7).

Пусть теперь p >1. Выберем Е так, чтобы выполнялось условие p-E >1. Тогда из (14) получаем >1 или u_n >1, следовательно, u_n ¹0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.

 

26# Интегральный признак Коши

Пусть члены знакоположительного числового ряда u₁+u₂+…+u_n… (7) не возрастают: u₁ ³ u₂ ≥…≥ u_n ≥… и пусть f(x) такая положительная, непрерывная, невозрастающая на промежутке [1;∞) функция, что f(1) = u₁, f( 2 ) = u₂,…, f (n)= = u_n,…. Тогда ряд (7) сходится или расходится одновременно с несобственным интегралом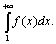

Доказательство. Построим график функции y=f(x) на отрезке [1; n ] и построим прямоугольник с основаниями [1;2], [2;3], …, [ n -1; n ] и высотами u₁, u₂,…, u_n-1, а также с высотами u₂,u₃,…,u_n.

S_n=u₁+u₂+…+u_n-1+u_n, S_впис=u₂^.1+u₃^.1+…+u_n^.1=u₂+u₃+…+u_n=S_n-u₁,

S_опис=u₁+u₂+…+ +u_n-1=S_n-u_n.

Площадь криволинейной трапеции S = . Получаем
S_n-u₁< < S_n-u_n. Отсюда

S_n < u₁ + (17)

и S_n >u_n+ (18)

Пусть сходится. Это означает, что существует конечный предел = Y. Соотношение (17) принимает вид: S_n < u₁ + Y при любом n. Это означает, что последовательность частичных сумм S_n ряда (7) ограничена и, следовательно, ряд (7) сходится. Пусть расходится. Это означает, что = ∞ и тогда из (18) следует, что последовательность частичных сумм S_n ряда (7) неограничена и, следовательно, ряд (7) расходится. Теорема доказана.

 

27# Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами.

Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на – 1.

Изучение знакопеременных рядов начнём с частного случая – знакочередующихся рядов.

Числовой ряд вида u₁-u₂+u₃-u₄+…+ +(- 1 )^{n- 1.} u_n+ …, где u_n – модуль члена ряда, называется знакочередующимся числовым рядом.

Если для знакочередующегося числового ряда

(19)

Выполняются два условия:

Члены ряда убывают по модулю u₁ > u₂ >…> u_n >…,

то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда.

Доказательство. Рассмотрим частичную сумму чётного числа членов ряда S_2n = (u₁-u₂)+(u₃-u₄)+…+(u_2n-1-u_2n).

По условию u₁ > u₂ >…> u_2n-1 > u_2n, то есть все разности в скобках положительны, следовательно, S_2n возрастает с возрастанием n и S_2n >0 при любом n.

С другой стороны S_2n = u₁-[(u₂-u₃)+(u₄-u₅)+…+(u_2n-2-u_2n-1)+u_2n]. Выражение в квадратных скобках положительно и S_2n >0, поэтому S_2n < u₁ для любого n. Таким образом, последовательность частичных сумм S_2n возрастает и ограничена, следовательно, существует конечный S_2n = S. При этом 0< S ≤ u₁.

Рассмотрим теперь частичную сумму нечётного числа членов ряда S_2n+1 = S_2n + u_2n+1. Перейдём в последнем равенстве к пределу при n→∞: S_2n+1= S_2n+ u_2n+1=S+ 0 =S. Таким образом, частичные суммы как чётного, так и нечётного числа членов ряда имеют один и тот же предел S, поэтому S_n = S, то есть данный ряд сходится. Теорема доказана.

Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно.

Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно.

 

28#Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают: u₁(x)+u₂(x)+…+u_n(x)+….

Если при x=x₀ функциональный ряд сходится, то x₀ называется точкой сходимости функционального ряда.

Множество всех точек сходимости функционального ряда называется его областью сходимости. Очевидно, что в области сходимости функционального ряда его сумма является функцией от x.

Степенным рядом называется функциональный ряд вида

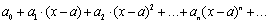, (24)

где a, a₀, a₁, a₂, …, a_n, … – некоторые числа, называемые коэффициентами степенного ряда.

Интервал сходимости - интервал, в каждой точке которого степенной ряд с действительными членами сходится, причем абсолютно. На каждом из концов этого интервала ряд может как сходиться (абсолютно или условно), так и расходиться. Вне этого интервала ряд расходится.

 

29# Всякая функция при соблюдении определенных условий в интервале, содержащим точку М₀, может быть представлена в нем в виде степенного ряда, и этот ряд будет ее рядом Тейлора.

Рядом Тейлора функции f (х) называется степенной ряд вида

Рядом Маклорена функции f (х) называется ряд

Ряды Тейлора и Маклорена есть разложение функции в ряд по степеням (x - x₀) и x соответственно, или представление функции в окрестности точек x₀ или x степенным рядом. Коэффициенты рядов Тейлора и Маклорена вычисляются через значения производных функции всех порядков в точках x = x₀ и x = 0 соответственно.