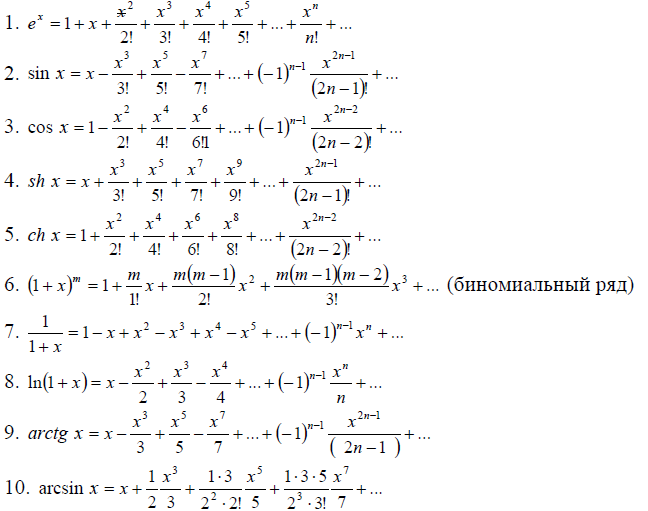
Ряды с 1-го по 5-ый сходятся для  , а ряды с 6-го по 10-ый для
, а ряды с 6-го по 10-ый для 
30# Разложение в ряд Маклорена элементарных функций

31# Приближенное вычисление определенных интегралов
Бесконечные ряды применяются также для приближенного вычисления определенных интегралов в случаях, когда первообразная не выражается в конечном виде через элементарные функции или нахождение первообразной сложно.
Пусть требуется вычислить  с точностью доɛ>0. Если подынтегральную функцию f(x) можно разложить в ряд по степеням х и интервал сходимости (-R;R)включит в себя отрезок [ а; b ], то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и ошибку при вычислении значений функций.
с точностью доɛ>0. Если подынтегральную функцию f(x) можно разложить в ряд по степеням х и интервал сходимости (-R;R)включит в себя отрезок [ а; b ], то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и ошибку при вычислении значений функций.
32# Функциональный ряд вида
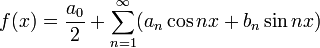 , где коэффициенты an, bn (n=0,1,2,…) определяются по формулам
, где коэффициенты an, bn (n=0,1,2,…) определяются по формулам

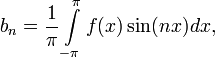

называется рядом Фурье функции f(x). Отметим, что всегда b0=0. Члены ряда можно записать в виде гармоник
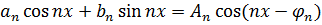 с амплитудой
с амплитудой  , частотой wn=n и фазой
, частотой wn=n и фазой 
Функция f(x) называется кусочно-монотонной на отрезке [a,b], если этот отрезок можно разбить на конечное число интервалов (a,x1),(x2,x3),…, (xk-1,b) таким образом, чтобы в каждом из них функция была монотонна.
33# Пусть функция z=f(x, y) определена в ограниченной замкнутой области D плоскости xOy. Разобьем D произвольным образом на n элементарных областей, имеющих области ∆σ1, ∆σ2,…, ∆σn и диаметры d1, d2,…, dn (наибольшее расстояние между точками границы области называется диаметром области). Выберем в каждой элементарной области произвольную точку Pk(ξk,ηk) и умножим значение функции в точке Pk на площадь этой области.
Выражение 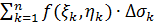 называется интегральной суммой для функции f(x, y) по области D. Если при
называется интегральной суммой для функции f(x, y) по области D. Если при  интегральная сумма имеет конечный предел
интегральная сумма имеет конечный предел  , то этот предел называется двойным интегралом от функции f(x, y) в области D и обозначается
, то этот предел называется двойным интегралом от функции f(x, y) в области D и обозначается 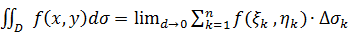 или
или 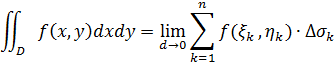
Геометрический смысл двойного интеграла: если f(x, y)>0 в области D, то двойной интеграл численно равен объему цилиндрического тела с основанием D, ограниченному сверху поверхностью z=f(x, y).
Если функция f(x, y) непрерывна в замкнутой области D, то двойной интеграл существует.
34# Пусть функция f(x, y, z) определена в ограниченной замкнутой пространственной области T. Разобьем T произвольным образом на n элементарных областей T1,T2,…,Tn с диаметрами d1, d2,…, dn и объемами ∆V1, ∆V2,…, ∆Vn. В каждой элементарной области возьмем произвольную точку 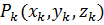 и умножим значение функции в точке Pk на объем этой области:
и умножим значение функции в точке Pk на объем этой области:  . Выражение
. Выражение  называется интегральной суммой для функции f(x, y, z) по области T.
называется интегральной суммой для функции f(x, y, z) по области T.
Предел интегральной суммы при стремлении к нулю наибольшего из диаметров элементарных областей называется тройным интегралом от функции f(x, y, z) по области T и обозначается: 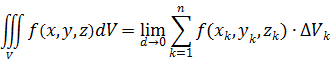
Основные свойства тройных интегралов аналогичны свойствам двойных интегралов. Если f(x, y, z) есть функция распределения плотности вещества в области T, то тройной интеграл численно равен массе всего вещества в этой области (физический смысл тройного интеграла).
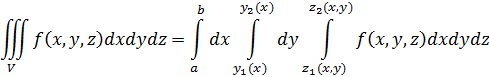 - формула для вычисления тройного интеграла в прямоугольных координатах.
- формула для вычисления тройного интеграла в прямоугольных координатах.