1. Средняя арифметическая постоянной равна самой постоянной: 
.
2. Если все варианты увеличить (уменьшить) на одну и туже постоянную, то средняя арифметическая увеличивается (уменьшится) на то же число: 
.
3. Если все варианты увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличивается (уменьшится) во столько же раз: 
.
4. Сумма отклонений вариантов от их средней арифметической равно нулю: 
5. Средняя арифметическая алгебраической суммы нескольких признаков равна такой же сумме средних арифметических этих признаков: 
6. Если ряд наблюдений состоит из нескольких групп, общая средняя равна средней арифметической групповых средних, причем весами являются объемы групп: 
,
где 
– общая средняя (средняя арифметическая всего ряда);
– групповая средняя i –ой группы, объем которой равен ni;
l – число групп.
Рассмотренные средние величины называются аналитическими. В статистическом анализе применяют так же и структурные или порядковые средние. К ним относятся мода и медиана.
Модой 
статистического ряда называется вариант, которому соответствует наибольшая частота.
Сложность в том, что редкая совокупность имеет единственную моду. (Например: 2, 6, 6, 8, 9, 9, 9, 10 – мода = 9).
Если два несмежных значения имеют равную и наибольшую в данной группе частоту, то у этого вариационного ряда есть две моды, такая группа называется бимодальной.
Особенность моды заключается в том, что она не меняется при изменении крайних членов ряда, т.е. обладает определенной устойчивостью к вариации ряда. Для интервального ряда:
, где
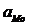– нижняя граница модального интервала;
– ширина интервала группировки;
– частота модального интервала;
– частота интервала, предшествующего модальному;
– частота интервала, следующего за модальным.
Медиана 
статистического ряда – это значение признака, приходящееся на середину ранжированного ряда наблюдений.
Для дискретного ряда с нечетным числом членов (n= 2 k +1) медиана равна серединному варианту Mе=xk+ 1, а для ряда с четным числом членов (n = 2 k) – полусумме двух серединных вариантов:
.
Для интервального ряда:
, где
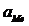– нижняя граница медианного интервала, к которому принадлежит медиана;
– половина объема выборки;
h – ширина медианного интервала;
–частота медианного интервала;
– накопленная частота интервала, предшествующего медианному.
Достоинство медианы заключается в том, что на нее не влияет изменение крайних членов вариационного ряда, если любой из них, меньший медианы, остается меньше нее, а любой, больший медианы, продолжает быть больше нее. Медиана предпочтительнее средней арифметической для ряда, у которого крайние варианты по сравнению с остальными оказались чрезмерно большими или малыми.
Мода наиболее просто вычисляется и при большом количестве измерений достаточно стабильна и близка к медиане и среднему. Медиана вычисляется по сложнее, особенно легко при ранжированных данных. При больших выборках предлагается сначала сгруппировать их, а потом вычислять медиану. Для определения моды и медианы не требуется знание всех остальных значений.
Пример. Найти моду и медиану интервального ряда.
| Возрастные группы | Число студентов 
| 
|
| До 20 лет | ||
| 20 — 25 | ||
| 25 — 30 | ||
| 30 — 35 | ||
| 35 — 40 | ||
| 40 — 45 | ||
| 45 лет и более | ||
| Итого |
Решение:
В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на этот интервал приходится наибольшая частота (1054).
Рассчитаем величину моды:
.
Это значит что модальный возраст студентов равен 27 годам.
Вычислим медиану. Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части (n /2 = 3462/2 = 1731). Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:
Это значит что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.
8.2. Показатели вариации как характеристики рассеяния
Средние величины не отражают изменчивости значений признака. Для оценки меры неоднородности (разброса, изменчивости) выборки наряду со средними значениями вычисляют и характеристики рассеяния.
Вариацией какого-либо параметра (показателя) в совокупности наблюдений называется различие его значений у разных элементов этой совокупности. Именно это свойство является объектом исследования большинства методов обработки ЭД.
Вариационный размах – это разность максимального и минимального значений статистического ряда: R=x max – x min.
Наибольший интерес представляют меры вариации (рассеяния) наблюдений вокруг средних величин.
Средним линейным отклонением статистического ряда называется средняя арифметическая абсолютных величин отклонений вариантов от их средней: 
Выборочной дисперсией s2 статистического ряда называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической:
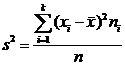или 
.
Для несгруппированного ряда (ni =1): 
.
Среднее квадратическое отклонение (стандартным отклонением) s статистического ряда – арифметическое значение корня квадратного из выборочной дисперсии:
или 
.
Размерность стандартного отклонения в отличие от размерности дисперсии совпадает с единицами измерения варьирующего признака, поэтому в практической статистике для того, чтобы охарактеризовать рассеяние признака используют обычно стандартное отклонение, а не дисперсию.
Свойства дисперсии:
1. Дисперсия постоянной равна нулю: 
.
2. Если все варианты увеличить (уменьшить) на одну и туже постоянную, то дисперсия не изменится: 
.
3. Если все варианты увеличить (уменьшить) в одно и то же число k раз, то дисперсия увеличивается (уменьшится) в k 2 раз: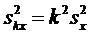 
.
4. Дисперсия равна разности между средней арифметической квадратов вариантов и квадратом средней арифметической: 
.
5. Если ряд наблюдений состоит из нескольких групп, общая дисперсия равна сумме средней арифметической групповых дисперсий (внутригрупповая дисперсия) и межгрупповой дисперсии («правило сложения дисперсий »):
,
где 
– общая дисперсия (дисперсия всего ряда);
– средняя арифметическая групповых дисперсий 
(внутригрупповая дисперсия);
– дисперсия i –ой группы 
, объем которой равен ni, 
- групповая средняя;
– межгрупповая дисперсия 
, где - общая средняя;
l- число групп.
Если требуется сопоставить стандартные отклонения со средними арифметическими этих признаков, то вводится относительный показатель, называемый коэффициентом вариации.
Коэффициент вариации – это процентное отношение среднего квадратического отклонения к средней арифметической:
Коэффициент вариации является относительной мерой рассеяния признака.
Коэффициент вариации используется и как показатель однородности выборочных наблюдений. Считается, что если коэффициент вариации не превышает 10%, то выборку можно считать однородной, т.е. полученной из одной генеральной совокупности.
8.3. Упрощенный способ расчета средней арифметической и дисперсии
Условными называют варианты, определяемые равенством
,
где с и h – специально подобранные числа:
ü с –ложный нуль (новое начало отсчета; чаще всего это середина серединного интервала, если серединных интервалов два, то за с берут середину одного из этих интервалов),
ü h – шаг, т.е разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба).
Упрощенный метод расчета характеристик выборки основан на замене первоначальных вариант на условные. Согласно свойствам средней арифметической и дисперсии
откуда
.
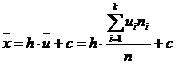
8.4. Начальные центральные моменты
Средняя арифметическая и дисперсия статистического ряда являются частными случаями более общих понятий – моментов статистического ряда.
Начальный моментk–го порядка статистического ряда определяется по формуле:
или 
Очевидно, что средняя арифметическая является моментом первого порядка статистического ряда: 
.
Центральный момент порядка s статистического ряда определяется по формуле:
или 
Нетрудно заметить, что при при s =1 первый центральный момент равен нулю, а при s =2 второй центральный момент - это выборочная дисперсия статистического ряда, т.е. 
.
Центральные моменты 
удобно рассчитывать по начальным моментам 
по формулам:
.
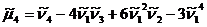Форма распределения выборочной совокупности характеризуется коэффициентом ассиметрии и эксцесса.
Коэффициентом асимметрии статистического ряда называется число:
.
Если 
, то распределение имеет симметричную форму, т.е. варианты равноудалены от и имеют одинаковую частоту. Если асимметрия – положительная, то распределение сдвигается влево, если отрицательная – вправо.
Эксцесс вариационного ряда называется число: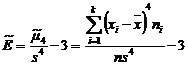 
Эксцесс – это мера крутости кривой распределения. Кривая распределения может быть островершинной, плосковершинной, средне вершинной. Если 
, то распределение имеет нормальную форму. Если эксцесс– положительный, то полигон имеет более крутую вершину по сравнению с нормальной кривой, если отрицательный – более пологую.
Эти четыре момента составляют набор особенностей распределения при анализе данных.
Глава 9. Оценки параметров распределения и их свойства
Одна из задач математической статистики: по имеющейся выборке оценить значения числовых характеристик исследуемой случайной величины.
Здесь речь идет об оценках (приближенных значениях) основных параметров распределения случайных величин: математического ожидания 
, дисперсии 
, среднего квадратического отклонения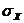 
случайной величины X, ковариации 
и коэффициента корреляции 
между двумя любыми случайными величинами X и Y, а также вероятности наступления случайного события p. Для удобства обозначим любой из перечисленных параметров символом 
(тета).
Статистической оценкой 
неизвестного параметра распределения называется любая функция от значений выборки 
, т.е. статистика.
Пусть распределение случайной величины 
(генеральной совокупности) задается вероятностями 
(для дискретной случайной величины) или плотностью вероятности 
(для непрерывной случайной величины), которые зависят от неизвестного параметра . Этим параметром может быть, например, параметр 
закона Пуассона или параметры а и 
нормального распределения. На практике о величине параметра можно судить по выборке 
объема n из генеральной совокупности.
Пусть по выборке объема найдена оценка. При повторении опыта происходит извлечение другой выборки того же объема из генеральной совокупности, и получается другая оценка неизвестного теоретического параметра. Повторяя опыт далее раз, получаем (в общем случае) различных чисел,,…,. Поэтому оценку можно рассматривать как случайную величину, которая может принимать значения,,…,.
Задача состоит в том, чтобы найти такую оценку , которая была бы в определенном смысле наиболее близкой к оцениваемому параметру θ.
Для того чтобы оценка давала «хорошие» приближения она должна быть: несмещенной, эффективной, состоятельной.
Несмещенной оценкой параметра θ называется статистическая оценка , если ее математическое ожидание совпадает со значением оцениваемого теоретического параметра при любом объеме выборки:
.
Смещенной оценкой называется оценка , математическое ожидание которой не равно значению теоретического параметра.
Таким образом, если 
, то мы будем получать при вычислении оценок систематические ошибки.
Асимптотически несмещенной оценкой называется статистическая оценка , если её математическое ожидание совпадает со значением оцениваемого теоретического параметра:
при 
.
Смещением оценки называется величина 
.
Свойство несмещенности является свойством оценок при фиксированном 
. Такая оценка не всегда дает хорошее приближение теоретического параметра, так как ее возможные значения могут быть значительно рассеяны относительно своего среднего значения. Это означает большую дисперсию 
, поэтому если в качестве оцениваемого параметра взять его несмещенную оценку, то распределение было бы установлено ошибочно. С минимизацией дисперсии оценки связано требование ее эффективности.
Состоятельной оценкой параметра θ называется статистическая оценка, которая при 
сходится по вероятности к истинному значению параметра, т.е.
,
Это необходимое свойство оценки, несостоятельными оценками пользоваться не рекомендуется.
Эффективной оценкой называется несмещенная статистическая оценка , если среди всех подобных оценок той же характеристики она имеет наименьшую дисперсию:
.
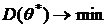Так для случайной величиной Х, имеющей нормальный закон распределения с дисперсией σ2,
ü нижняя граница для дисперсий различных несмещенных оценок математического ожидания равна 
,
ü нижняя граница для дисперсий различных несмещенных оценок дисперсии равна 
.
Для случайной величиной Х, выражающеей число наступлений события А в одном испытании ,и имеющей закон распределения
| xi | ||
| рi | q | р |
ü нижняя граница для дисперсий различных несмещенных оценок вероятности р равна 
.
Различают два вида оценок – точечные и интервальные.
Точечными называют такие оценки, которые характеризуются одним числом.
Интервальные оценки задаются двумя числами, определяющими вероятный диапазон возможного значения параметра.
9.1. Точечная оценка параметров распределения
Точечная оценка предполагает нахождение единственной числовой величины, которая и принимается за значение параметра. Такую оценку целесообразно определять в тех случаях, когда объем ЭД достаточно велик. При малом объеме ЭД точечные оценки могут значительно отличаться от истинных значений параметров, что делает их непригодными для использования.
9.1.1. Точечная оценка математического ожидания
В качестве приближенного значения (статистической оценки) математического ожидания будем использовать выборочную среднюю 
.
Будем рассматривать 
как случайную величину 
, а х 1, х 2,…, хп (значения исследуемой случайной величины, составляющие выборку)– как независимые, одинаково распределенные случайные величины Х 1, Х 2,…, Хп, имеющие математическое ожидание а.
Выясним состоятельность, несмещенность и эффективность выборочной средней какточечной оценки математического ожидания.
Несмещенность
Теорема. Пусть М (Х 1)=…= М (Хn)= М (Х), тогда средняя арифметическая
является несмещенной оценкой математического ожидания М (Х).
Доказательство. Если М (Х 1)=…= М (Хn)= М (Х), то при любом n имеет место следующее свойство математического ожидания
,
то есть 
.
Таким образом, если 
, а 
, то 
является несмещенной оценкой математического ожидания М (Х).
Выборочное среднее является не только несмещенной, но и состоятельной оценкой математического ожидания.
Состоятельность.
Теорема. Пусть результаты Х 1,…, Хn наблюдений величины Х независимые случайные величины и М (Х 1)=…= М (Хn)= М (Х), и дисперсии D (Х 1)=… D (Хn) конечны. Тогда средняя – состоятельная оценка математического ожидания М (Х).
Если предположить, что Х 1, Х 2,…, Хп имеют ограниченные дисперсии, то из теоремы Чебышева следует, что их среднее арифметическое, то есть , при увеличении п стремится по вероятности к математическому ожиданию а каждой их величин, то есть к М (Х):
которое, учитывая условие М (Х 1)=…= М (Хn)= М (Х), можно записать
.
Из определения состоятельности следует, что если , а , то выборочная средняя является состоятельной оценкой математического ожидания.
Эффективность.
Напомним, что свойство эффективности рассматривается только для несмещенных оценок. Докажем эффективность для случая, когда случайная величина Х имеет нормальный закон распределения.
Теорема. Пусть случайная величина Х имеет нормальный закон распределения и при этом результаты Х 1,…, Хn ее наблюдений независимы, а так же выполняются условия: М (Х 1)=…= М (Хn)= М (Х) и D (Х 1)=…= D (Хn)= D (Х). Тогда средняя арифметическая 
– это несмещенная эффективная оценка математического ожидания М (Х).
Доказательство. Для доказательства эффективности докажем, что ее дисперсия совпадает с минимальной границей, равной в случае нормального распределения .
.
Таким образом, - несмещенная эффективная оценка математического ожидания М (Х).
9.1.2. Точечная оценка дисперсии
Наряду с выборочной дисперсией
в качестве приближенного значения (возможной оценки) генеральной дисперсии будем использовать величину
,
которая связана с s2 соотношением
Выясним их состоятельность, несмещенность и эффективность.
Состоятельность.
Теорема. Пусть результаты Х 1,…, Хn наблюдений величины Х независимые случайные величины и М (Х 1)=…= М (Хn)= М (Х), а дисперсии D (Х 1)=… D (Хn)= D (Х), а центральные моменты второго и третьего порядков величины Х конечны. Тогда при любом ε>0 имеет место равенство:
т.е. s 2 – состоятельная оценка генеральной дисперсии D (Х) и
,
т.е. 
– состоятельная оценка генеральной дисперсии D (Х).
Несмещенность.
Покажем, что s 2 является смещенной оценкой дисперсии D (Х), так как при n =2 М (s 2)≠ D (Х).
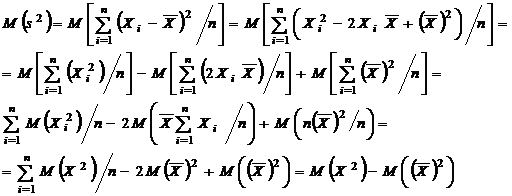
но
.
Таким образом, 
– s 2 является смещенной оценкой дисперсии D (Х) и смещение равно 
.
Теорема. Пусть результаты Х 1,…, Хn наблюдений величины Х независимы, а М (Х 1)=…= М (Хn)= М (Х) и дисперсии D (Х 1)=… D (Хn)= D (Х). Тогда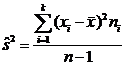 
– несмещенная оценка дисперсии D (Х).
Доказательство. Найдем 
:
.
Итак при любом n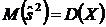 
, т.е. если 
, а 
, то является несмещенной оценкой дисперсии D (Х).
Эффективность.
Пусть случайная величина Х имеет нормальный закон распределения. Для доказательства эффективности докажем, что ее дисперсия совпадает с минимальной границей, равной в случае нормального распределения .
Предположим, что результаты Х 1,…, Хn наблюдений случайной величины Х независимы и имеют тот же закон распределения, что и случайная величина Х. При выполнении этих условий выполняется соотношение: 
. Поэтому
.
Так как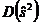 
не совпадает с нижней границей, то будучи несмещенной оценкой дисперсии D(Х), не является эффективной оценкой.
9.1.3. Частость как точечная оценка вероятности события
Обозначим через р неизвестную вероятность появления события А в единичном испытании. Найдем приближенное значение w вероятности р. Проведем n независимых испытаний по схеме Бернулли. Пусть m – количество испытаний, в которых произошло событие А. Тогда w= m / n – это частость появления события А. выясним, какими свойствами обладает w как точечная оценка вероятности р события.
Теорема. Пусть m – число наступлений события А в n независимых испытаниях, р - вероятность наступления события А в каждом из испытаний. Тогда w= m / n – состоятельная, несмещенная и эффективная оценка вероятности р.
Состоятельность.
Для испытаний по схеме Бернулли справедлива теорема Бернулли, согласно которой для любого ε>0 имеет место равенство
.
Из определения состоятельности следует, что если 
, а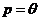 
, то w= m / n – состоятельная оценка вероятности р.
Несмещенность
Найдем математическое ожидание частости:
.
Таким образом, при любом фиксированном числе n испытаний 
. Это означает, что w= m / n является несмещенной оценкой вероятности р.
Эффективность.
Сопоставим с результатом единичного испытания случайную величину
| Х | xi | ||
| рi | q | р |
Последовательность n испытаний по схеме Бернулли – это n независимых наблюдений случайной величины Х, проводимых в одинаковых условиях, тогда нижняя граница для дисперсий различных несмещенных оценок вероятности р равна р(р-1)/n.
Теперь найдем дисперсию частости:
.
Так как 
совпадает с минимальной границей, то w= m/ n является несмещенной и эффективной оценкой вероятности р.
9.2. Методы оценки параметров распределения
Существует несколько методов нахождения точечной оценки параметров, наиболее употребительными из них являются методы максимального (наибольшего) правдоподобия, моментов и метод наименьших квадратов.
9.2.1. Метод максимального правдоподобия (ММП)
Метод предложен Р. Фишером в 1912г. Основу метода составляет функция правдоподобия как функция параметра θ, выражающаявероятность (плотность) совместного появления результатов выборки наблюдений x 1, x 2, …, xn.
L (х 1, х 2 …, хn ; θ) = p (х 1, θ) p (х 2, θ) … p (хп, θ)
или
L (х 1, х 2 …, хn ; θ) = f (х 1, θ) f (х 2, θ) … f (хп, θ).
Тогда в качестве точечной оценки 
параметра θ принимают такое его значение
= θ (х 1, х 2, …, хп),
при котором функция правдоподобия достигает максимума. Оценку называют оценкой наибольшего правдоподобия.
В качестве оценки неизвестного параметра следует взять такое значение 
, которое обращает функцию правдоподобия в максимум.
Пусть Х – дискретная случайная величина, которая в результате п испытаний приняла значения х 1, х 2, …, хп. Предположим, что нам известен закон распределения этой величины, определяемый параметром θ, но неизвестно численное значение этого параметра. Найдем его точечную оценку.
Поскольку функции L и ln L достигают максимума при одном и том же значении θ, удобнее искать максимум ln L – логарифмической функции правдоподобия. Для этого нужно:
1) найти производную 
;
2) приравнять ее нулю (получим так называемое уравнение правдоподобия) и найти критическую точку;
3) найти вторую производную 
, если она отрицательна в критической точке, то это – точка максимума.
Достоинства метода наибольшего правдоподобия: полученные оценки состоятельны (хотя могут быть смещенными), распределены асимптотически нормально при больших значениях п и имеют наименьшую дисперсию по сравнению с другими асимптотически нормальными оценками; если для оцениваемого параметра θ существует эффективная оценка , то уравнение правдоподобия имеет единственное решение ; метод наиболее полно использует данные выборки и поэтому особенно полезен в случае малых выборок.
Недостаток метода наибольшего правдоподобия: сложность вычислений.
Пример. Будем считать, что случайная величина Х, имеет нормальное распределение с плотностью вероятности
По выборке значений найдены фактические значения оценок математического ожидания и дисперсии: 
=27,51, s 2 = 0,91.
Необходимо найти оценки максимального правдоподобия параметров а и 2 этого распределения.
Решение. Функция правдоподобия для выборки ЭД объемом n
.
Логарифм функции правдоподобия
.
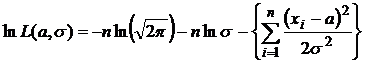Система уравнений для нахождения оценок параметров
Из первого уравнения следует:
и 
,
т.е. среднее арифметическое является оценкой максимального правдоподобия для математического ожидания. Из второго уравнения можно найти
,
т.е. оценку максимального правдоподобия для дисперсии – выборочную дисперсия s 2, являющуюся смещенной оценкой.
Для проверки того, что полученные оценки максимизируют значение функции правдоподобия, возьмем вторые производные
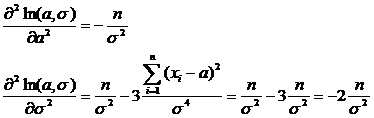
Вторые производные от функции ln L (а,) независимо от значений параметров меньше нуля, следовательно, найденные значения параметров являются оценками максимального правдоподобия.
9.2.2. Метод моментов
Метод предложен К. Пирсоном в 1894 г. Метод моментов основан на том, что начальные и центральные эмпирические моменты являются состоятельными оценками соответственно начальных и центральных теоретических моментов, поэтому можно приравнять теоретические моменты соответствующим эмпирическим моментам того же порядка.
Алгоритм метода:
ü выбирается столько эмпирических моментов, сколько требуется оценить неизвестных параметров распределения;
ü вычисленные по ЭД оценки моментов приравниваются к теоретическим моментам;
ü параметры распределения определяются через моменты, и составляются уравнения, выражающие зависимость параметров от моментов, в результате получается система уравнений. Решение этой системы дает оценки параметров распределения генеральной совокупности.
Например, если известный вид плотности распределения f (x, θ 1, θ 2) определяется двумя неизвестными параметрами θ 1 и θ 2, то требуется составить два уравнения, например
, 
.
Отсюда
система двух уравнений с двумя неизвестными θ 1 и θ 2. Ее решениями будут точечные оценки 1 и 2 – функции вариант выборки:
1= y1(х 1, х 2, …, хп