Пусть в пространстве задана ось l (направленная прямая) и т. М, не лежащая на данной оси. Проекцией т. М на ось l называется основание М1 перпендикуляра (нормали), опущенного из т. М на ось l. Если т. М лежит на оси, то проекция совпадет с точкой.
Дан вектор АВ-, не равный 0, и ось l. Обозначу через А1 и В1 проекции точек на ось. Получился отрезок А1В1 меньшей длины, чем сам вектор. Проекцией АВ- на ось l называется положительное число IА1В1I, если вектор и ось одинаково направленны; или же отрицательное число –IА1В1I, если они противоположны. А если т. А1 и В1 совпадают, то проекция равна 0.
Обозначается: пр.lАВ- Можно записать символически: пр.lАВ-=IА1В1I, если А1В1 (стрелки вверх, вверх) l или =- IА1В1I, если А1В1 (стрелки вниз, вверх) l.
Угол (у) между АВ- и осью l получу сместив начало АВ- на ось. Угол рассматривается обычно в промежутке от 0 до пи.
Свойства проекций.
1. Проекция а- на ось l равна произведению Ia-I на cos угла между вектором и осью: пр.lа-=Ia-I*cos<у
1 Следствие: Проекция >0, если вектор образует с осью острый угол; <0, если тупой угол; =0, если y=90.
2 Следствие: Проекции равных векторов на одну и ту же ось равны.
2. Проекция суммы n векторов на одну ось равна сумме их проекций на эту ось:
пр.l(a-+b-+c-)=пр.lа-+пр.lb-+пр.lc-
3. При умножении вектора на число его проекция на ось так же умножается на это число:
пр.l(h*a-)=h*пр.la-
16. Разложение вектора по ортам координатных осей. Координаты вектора.
Дана прямоугольная система координат Ох, Оу, Оz в трехмерном пространстве. Выделю единичные вектора (орты) на каждой оси и обозначу i, j, k. Начало произвольного вектора совмещу с началом координат. Обозначу проекции вектора на оси:
пр.Оха-=ах пр.Оуа-=ау пр.Оzа-=аz
Нужно указать, что: а-=ах*i+ay*j+az*k Это разложение любого вектора по ортам координатных осей. Чсла ах, ау, аz называются координатами вектора а-, т. е. координаты вектора – его проекции на ось. Данное равенство также записывается: а-=(ах;ay;az).
· Формула вычисления модуля вектора через его координаты. Направляющие косинусы.
Зная проекции вектора, можно найти его модуль (длину): Ia-I=квадратный корень из а2х+а2у+а2z
Модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Рассмотрев углы, образованные а- с Ох, Оу, Оz, обозначу их как: <a, <B, <y. По 1 свойству проекций вектора на ось имеем: ах=Ia-I*cos<a ay=Ia-I*cos<B az=Ia-I*cos<y Выражу косинусы:
cos<a= ах/ Ia-I cos<B= ay/ Ia-I cos<y= az/Ia-I Эти числа и есть направляющие косинусы.
Нужно указать, что: cos2<a+ cos2<B + cos2<y =1
· Действия над векторами, заданными своими координатами: линейные операции, равенства.
Линейные операции.
Линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями векторов (свойства 2 и 3). Т. к.:
а-=(ах;ay;az) или а-=ах*i+ay*j+az*k
в-=(вх;вy;вz) или в-=вх*i+вy*j+вz*k
То нужно записать:
1. а- + в-=(ах + вх)*i+(ay + ву)*j+(az + вz)*k
2. ha-=h*ах*i+h*ay*j+h*az*k ha-=(h*ах;h*ay;h*az)
При сложении векторов складываются одноименные координаты, при умножении вектора на число умножаются все его координаты на число.
Равенство векторов.
Из определения вектора, как наравленного отрезка, следует, что два вектора равнытогда и только тогда, когда равны соответствующие координаты этих векторов:
а-=(ах;ay;az) в-=(вх;вy;вz) а-= в- если ах= вх, ay=вy, az=вz
· Условие коллинеарности векторов.
Условие коллинеарности можно записать в виде: а-=h*в-, где h принадлежит R
а- (палки вверх) в- если а-=h*в-
Разложу по ортам координатных осей:
ах*i+ay*j+az*k= h*вх*i+h*вy*j+h*вz*k Свяжу с условием одноименные координаты:
из ах=h*вх, ау=h*ву, аz=h*вz следует h=ах/вх, h=аy/вy, h=аz/вz
Значит, h=ах/вх=аy/вy=аz/вz Это и есть условие коллинеарности векторов в координатной форме. Таким образом 2-а вектора коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны.
· Скалярное произведение векторов. Свойства.
Скалярное произведение векторов.
Скалярное произведение 2-х ненулевых векторов – число, равное произведению длин этих векторов на косинус угла между ними. Результат – число.
а-*в-=Ia-I*Iв-I*cos<фи где фи – угол между векторами
Можно преобразовать: из Ia-I*cos<фи=пр.в-а- и Iв-I*cos<фи=пр.а-в- следует
а-*в-= пр.в-а-* Iв-I или а-*в-= пр.а-в-*Ia-I
Т. е. скалярное произведение 2-х векторов равно модудю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
Свойства.
1. Переместительное а-*в-=в-* а-
2. Сочетательное, относительно скалярного множителя
Если h принадлежит R, то (h*а-)*в-= h*(а-*в-)
3. Распределительное а-*(в-+с-)= а-*в-+ а-*с-
4. Скалярный квадрат вектора равен квадрату его длины
а2-= а-*а-= Ia-I*Ia-I*cos0= Ia-I2 В частности i2=j2=k2=1
Если а- возвести скалярно в квадрат, а затем извлечь корень, то получится не первоначальное число, а число, равное модулю этого вектора: квадратный корень из а2-= Ia-I
5. Если а- и в- (не нулевые) взаимно перпендикулярны, то их скалярное произведение равно 0, т. к. cos<90=0.
Справедливои обратное утверждение: если скалярное произведение векторов, не равных 0, равно 0, то эти векторы взаимно перпендикулярны. В частности:
i*j=0 i*k=0 j*k=0 i*j=i*k=j*k=0
· Выражение скалярного произведения векторов через координаты. Угол между векторами. Условие ортогональности.
Выражение скалярного произведения через координаты.
Пусть заданы а- и в- через разложение по ортам координат осей
а-=ах*i+ay*j+az*k в-=вх*i+вy*j+вz*k
Найду скалярное произведение векторов, перемножая их как многочлены (согласно свойствам 1,2,3 скалярного произведения). При умножении будем пользоваться таблицей скалярного произведения i, j, k (по свойствам 4 и 5):
| i | j | k | |
| i | |||
| j | |||
| k |
а-*в-= (ах*i+ay*j+az*k)*(вх*i+вy*j+вz*k)=ах*вх+ay*вy+az*вz
Скалярное произведение векторов равно сумме произведений их одноименых координат.
Угол между векторами.
а-*в-=Ia-I*Iв-I*cos<фи
cos<фи=(а-*в-)/(Ia-I*Iв-I)=(ах*вх+ay*вy+az*вz)/(квадр. корень из а2x+a2y+a2z)*(квадр. корень из вх2+вy2+вz2)
Условие ортогональности.
Следствие: Если фи=90 (а- в-), то а-*в-=0, т. е. ах*вх+ay*вy+az*вz=0 Это условие перпендикулярности, или ортогональности, векторов в трехмерной системе координат.
· Векторное произведение. Свойства.
Векторное произведение
Векторным произведением двух векторов 
называется вектор, который
перпендикулярен плоскости перемножаемых векторов;
направлен туда, откуда видится поворот первого множителя вектора ко второму против часовой стрелки;
его модуль равен произведению модулей перемножаемых векторов на синус угла между ними:
Свойства:
Векторное произведение коллинеарных векторов равно нулю.
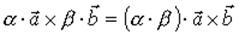, где α и β числа,
,
.
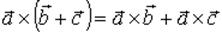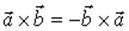· Выражение векторного произведения через координаты.
Векторное произведение в координатах
Представим перемножаемые векторы в разложении по базисным векторам декартовой системы координат и перемножим их, воспользовавшись свойствами векторного произведения,
· Выражение векторного произведения через координаты
Условие комплонарности.Условие паралейности
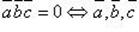- компланарны.
Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
· Определение площади параллелограмма,припомощи векторного произведения
Формуле вычисления площади параллелограмма можно придать более простой вид через скалярное произведение:
или окончательно
· Смешаное произведение вектора.Геометрический смысл произведение.
Рассмотрим произведение векторов а, b и с, составленное следующим образом: (ахb)•с. Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторноскалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.
Геометрический смысл выражения (ахb)*с. Построим параллелепипед, ребрами которого являются векторы а, b, с и вектор d =ахb
Имеем: (а х b) • с = d • с = |d| • прdс, |d|=|а х b| =S, где S — площадь параллелограмма, построенного на векторах а и b, прdс = Н Для правой тройки векторов и прdс = - Н для левой, где Н— высота параллелепипеда. Получаем: (axb)*c =S *(±H), т. е. (axb)*c =±V, где V — объем параллелепипеда, образованного векторами а, b и с.
Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.
27.
Св-ва смешаного произведения
1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b)•с=(b х с)•а=(с х а)•b.
Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер
2. Смешанное произведение не меняется при перемене местами знаков вкторного и скалярного умножения, т. е. (ахb)•с=а*(bx с).
Действительно, (ахb)•с=±V и а•(b хс)=(b хс)•а=±V. Знак в правой части этих равенств берем один и тот же, так как тройки векторов а, b, с и b, с, а — одной ориентации.
Следовательно, (a хb)•с=a (b хс). Это позволяет записывать смешанное произведение векторов (а х b)с в виде abc без знаков векторного, скалярного умножения.
3. Смешанное произведение меняет свой знак при перемене мест любых вух векторов-сомножителей, т. е. abc =-acb, abc =-bac, abc =-cba.
Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.
4.Смешанное произведение ненулевых векторов а, b и с равно нулю огда и только тогда, когда они компланарны.
Если abc =0, то а, b и с— компланарны.
Допустим, что это не так. Можно было бы построить параллелепипед с объемом V¹ 0. Но так как abc =±V, то получили бы, что abc¹0. Это противоречит условию: abc =0.
Обратно, пусть векторы а, b, с — компланарны. Тогда вектор d =ахb будет перпендикулярен плоскости, в которой лежат векторы а, b,с, и следовательно, d ^с. Поэтому d •с=0, т. е. abc =0.
28.
Выражение смешанного произведения через координаты
Пусть заданы векторы a =ахi +ayj +azk, b =bxi +byj +bzk, с=cxi +cyj +czk. Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:
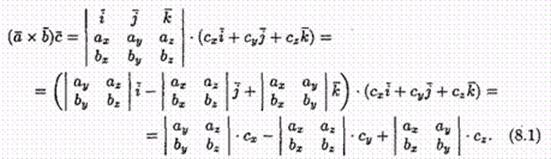
Полученную формулу можно записать короче:
так как правая часть равенства (8.1) представляет собой разложение определителя третьего порядка по элементам третьей строки.
Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.
29)
Общее уравнение прямой
Общее уравнение прямой линии на плоскости в декартовых координатах:
где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.
При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде:
Всякое уравнение первой степени относительно х и у, т.е. уравнение вида Ax+By+C=0
(где А, В и С- постоянные коэффициенты, причем А2+В2≠0) определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.
Частные случаи:
1. С=0; А≠0; В≠0. Прямая, определяемая уравнением Ах+Ву=0, проходит через начало координат.
2. А=0, В≠0; С≠0. Прямая, определяемая уравнением Ву+С=0 (или у=b, где), параллельна оси (ох).
3. В=0; А≠0; С≠0. Прямая, определяемая уравнением Ах+С=0, параллельна оси Оу.
4. В=С=0; А≠0. Прямая определяемая уравнением Ах=0 (или x=0 поскольку А≠0), совпадает с осью Оу.
5. А=С=0; В≠0. Прямая, определяемая уравнением Ву=0 (или у=0, поскольку В≠0), совпадает с осью Oх.
Если в общем уравнении прямой В≠0, то, разрешив его относительно у, получим уравнение вида y=kx+в. Его называют уравнением с угловым коэффициентом поскольку где -угол, образованный прямой с положительным направлением оси Oх. Свободный член уравнения в равен ординате точки пересечения прямой с осью Oу.
30.
Пусть прямые l1 и l2 заданы общими уравнениями
A1x + В1у + C1 = 0 и А2х + В2 y + С2 = 0.
Согласно формуле: 
и, следовательно, косинус угла φ между прямыми l1 и l2 может быть вычислен по формуле:
Записав правую часть формулы через координаты, получим: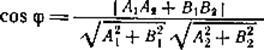 
Прямые с нормальными векторами n1 и n2: (Условия параллельности и перпендикулярности двух прямых)
а) параллельны тогда и только тогда, когда векторы n1 и n2 коллинеарны;
б) перпендикулярны тогда и только тогда, когда векторы n1 и n2 перпендикулярны, т. е. когда n1 • n2 = 0.
Отсюда получаем необходимые и достаточные уcловия параллельности и перпендикулярности двух прямых, заданных общими уравнениями.
Для того чтобы прямые
A1x + В1у + C1 = 0 и А2х + В2 y + С2 = 0
были:
а) параллельны, необходимо и достаточно, чтобы
б) перпендикулярны, необходимо и достаточно, чтобы
A1A2 + В1В2 = 0
31.
Пусть в пространстве заданы две точки M 1 (x 1, y 1, z 1) и M2 (x 2, y 2, z 2), тогда уравнение прямой, проходящей через эти точки:
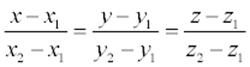
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.
На плоскости записанное выше уравнение прямой упрощается:
если х 1 ≠ х2 и х = х 1, если х 1 = х2.
Дробь 
= k называется угловым коэффициентом прямой.
Уравнение прямой по точке и направляющему вектору
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.
Определение. Каждый ненулевой вектор (α1, α2), компоненты которого удовлетворяют условию А α1 + В α2 = 0 называется направляющим вектором прямой
Ах + Ву + С = 0.
Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).
Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В.
Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.
при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:
х + у - 3 = 0