ВЫСШАЯ МАТЕМАТИКА
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МЕТЕМАТИЧЕСКАЯ СТАТИСТИКА
МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ
для студентов факультета
непрерывного профессионального образования
(экономические специальности)
Ижевск 2006
Методические указания рассмотрены и рекомендованы к изданию кафедрой высшей математики (протокол №2 от 5 сентября 2003 г.).
Рецензенты:
канд. ф.-м. наук, доцент Хохряков Н.В.
канд. ф.-м. наук, доцент Юберев Н.Н.
Составитель:
зав. кафедрой высшей математики ИжГСХА, доцент Карпова В.С.
Компьютерный набор и технический редактор Тылюдина Е.В.
Оглавление:
| 1. Варианты заданий……………………………………………………………… | …3 |
| 2. Контрольная работа №4 (задания)…………………………………………..... | …4 |
| примеры решения задач……………………………………………. | …8 |
| формулы…………………………………………………………….. | ..14 |
| вопросы и задачи для зачета……………………………………..... | ..18 |
| 2. Контрольная работа №5 (задания)…………………………………………..... | ..21 |
| примеры решения задач……………………………………………. | ..28 |
| формулы…………………………………………………………….. | ..38 |
| вопросы и задачи для зачета………………………………………. | ..42 |
ВАРИАНТЫЗАДАНИЙ
Студент выполняет тот вариант контрольной работы, который совпадает с последней цифрой его учебного шифра. При этом, если предпоследняя цифра его учебного шифра есть число нечетное (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в таблице 1. Если предпоследняя цифра учебного шифра есть число четное или ноль (2, 4, 6, 8, 0), то номера задач даны в таблице 2.
Таблица 1
| Номер варианта | Номера задач для контрольных работ | |
| Работа №4 | Работа №5 | |
| 251, 271, 281, 291, 301 | 1, 11 | |
| 252, 272, 282, 292, 302 | 2, 18 | |
| 253, 273, 283, 293, 303 | 3, 19 | |
| 254, 274, 284, 294, 304 | 4, 12 | |
| 255, 275, 285, 295, 305 | 5, 20 | |
| 256, 276, 286, 296, 306 | 6, 21 | |
| 257, 277, 287, 297, 307 | 7, 22 | |
| 258, 278, 288, 298, 308 | 8, 23 | |
| 259, 279, 289, 299, 309 | 9, 24 | |
| 260, 280, 290, 300, 310 | 10, 25 |
Таблица 2
| Номер варианта | Номера задач для контрольных работ | |
| Работа №4 | Работа №5 | |
| 261, 272, 283, 294, 305 | 1, 11 | |
| 262, 273, 284, 295, 306 | 2, 18 | |
| 263, 274, 285, 296, 307 | 3, 19 | |
| 264, 275, 286, 297, 308 | 4, 12 | |
| 265, 276, 287, 298, 309 | 5, 20 | |
| 266, 277, 288, 299, 310 | 6, 21 | |
| 267, 278, 289, 300, 301 | 7, 22 | |
| 268, 279, 290, 291, 302 | 8, 23 | |
| 269, 280, 281, 292, 303 | 9, 24 | |
| 270, 281, 282, 293, 304 | 10, 25 |
Контрольная работа №4
251. В читальном зале имеется 6 учебников по теории вероятностей, из которых 3 в мягком переплете. Библиотекарь взял два учебника. Найти вероятность того, что оба учебника окажутся в мягком переплете.
252. Студент знает ответы на 20 из 25 вопросов программы. Найти вероятность того, что он знает ответы на предложенные ему экзаменатором три вопроса.
253. Для некоторой местности в июле шесть пасмурных дней. Найти вероятность того, что первого и второго июля будет ясная погода.
254. Из 200 рабочих норму выработки не выполняют 15 человек. Найти вероятность того, что два случайно выбранных рабочих не выполняют норму.
255. Три стрелка стреляют по мишени. Вероятность попадания в цель первым стрелком равна 0,6, вторым – 0,7, третьим – 0,8. Найти вероятность того, что при одном выстреле попадут в цель: а) все три стрелка; б) попадет хотя бы один из них.
256. В ящике лежат 20 электрических лампочек, из которых 2 нестандартные. Найти вероятность того, что взятые одна за другой две лампочки окажутся стандартными.
257. Одновременно бросаются две игральные кости. Найти вероятность того, что на каждой кости появится нечетное количество очков.
258. Из заготовленной для посева пшеницы зерно первого сорта составляет 40%, второго сорта – 50%, третьего сорта – 10%. Вероятность того, что взойдет зерно первого сорта равна 0,8, второго – 0,5, третьего – 0,3. Найти вероятность того, что взойдет наугад взятое зерно.
259. В магазин поступили телевизоры из трех заводов. Вероятность того, что телевизор изготовлен на первом заводе, равна 0,3, на втором – 0,2, на третьем – 0,5. Вероятность того, что телевизор окажется бракованным, для первого завода равна 0,2, для второго – 0,1, для третьего – 0,3. Найти вероятность того, что наугад взятый телевизор окажется небракованным.
260. В мастерской на трех станках изготавливаются однотипные детали. Вероятность безотказной работы первого станка равна 0,8, второго – 0,7, третьего – 0,9. Вероятность изготовления бракованной детали на первом станке равна 0,2, на втором – 0,3, на третьем – 0,1. Найти вероятность того, что наугад выбранная деталь окажется стандартной.
261. Вероятность попадания в цель при одном выстреле равна 0,7. Производится 4 выстрела. Найти вероятность того, что цель будет поражена: а) три раза; б) не более двух раз.
262. Вероятность всхожести пшеницы равна 0,8. Какова вероятность того, что из 5 семян взойдет не менее 3?
263. Вероятность попадания в цель при одном выстреле равна 0,8. Написать закон распределения вероятностей попаданий в цель при 5 выстрелах и построить многоугольник распределения вероятностей.
264. Всхожесть семян пшеницы составляет 90%. Определить наиболее вероятное число всходов из 200 посеянных семян.
265. Семена пшеницы содержат 0,2% сорняков. Найти вероятность того, что в 1000 семян будет 6 семян сорняков.
В задачах 266–270 дана вероятность р того, что семя злака прорастет. Найти вероятность того, что из п посеянных семян прорастет ровно  семян.
семян.
266. 
267. 
268. 
269. 
270. 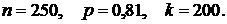
В задачах 271–280 дана вероятность р появления события А в каждом из п независимых испытаний. Найти вероятность того, что в этих испытаниях событие А появится не менее  раз и не более
раз и не более  раз.
раз.
271. 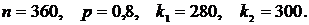
272. 
273. 
274. 
275. 
276. 
277. 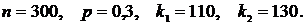
278. 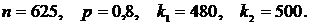
279. 
280. 
В задачах 281–290 задан закон распределения дискретной случайной величины Х (в первой строке указаны возможные значения величины Х, во второй строке даны вероятности р этих значений). Найти: 1) математическое ожидание  ; 2) дисперсию
; 2) дисперсию  ; 3) среднее квадратическое отклонение
; 3) среднее квадратическое отклонение  .
.



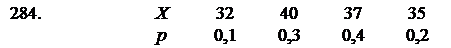






В задачах 291–300 случайная величина Х задана интегральной функцией распределения  . Найти: 1) дифференциальную функцию распределения
. Найти: 1) дифференциальную функцию распределения  ; 2) математическое ожидание
; 2) математическое ожидание  ; 3) дисперсию
; 3) дисперсию  .
.
291. 
292. 
293. 
294. 
295. 
296. 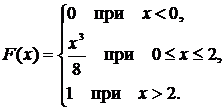
297. 
298. 
299. 
300. 
301. Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно 0,25 мм. Стандартными считаются детали, размер которых заключен между 199,5 мм и 200,5 мм. Найти процент стандартных деталей.
302. Средний диаметр стволов деревьев на некотором участке равен 25 см, среднее квадратическое отклонение равно 5 см. Считая диаметр ствола случайной величиной, распределенной нормально, найти процент деревьев, имеющих диаметр свыше 20 см.
303. Процент всхожести семян равен 90%. Оценить вероятность того, что из 1000 посеянных семян взойдет от 850 до 950 семян включительно.
304. Среднее квадратическое отклонение нормально распределенной случайной величины равно 0,5. Найти вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине не превосходит 1.
305. Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 150 мм и средним квадратическим отклонением 0,5 мм. Какую точность размера детали можно гарантировать с вероятностью 0,95.
306. Средний вес зерна равен 0,2 г, среднее квадратическое отклонение равно 0,05 г. Определить вероятность того, что вес наудачу взятого зерна окажется в пределах от 0,16 г до 0,22 г.
307. Норма высева семян на 1 га равна 200 кг. Фактический расход семян на 1 га колеблется около этого значения со средним квадратическим отклонением 10 кг. Определить количество семян, обеспечивающих посев на площади 100 га с гарантией 0,95.
308. Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно 0,25 мм. Стандартными считаются детали, размер которых заключен между 199,5 мм и 200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилась и характеризуется средним квадратическим отклонением 0,4 мм. На сколько повысился процент бракованных деталей?
309. Масса яблока, средняя величина которой равна 150 г, является нормально распределенной случайной величиной со средним квадратическим отклонением 20 г. Найти вероятность того, что масса наугад взятого яблока будет заключена в пределах от 130 г до 180 г.
310. Устройство состоит из 20 однотипных независимо работающих элементов. Вероятность безотказной работы каждого элемента за 10 часов равна 0,9. Оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом отказов за 10 часов окажется меньше двух.
Примеры решения задач
Задача 1. Вероятность всхожести семян пшеницы равна 0,9. Какова вероятность того, что из четырех посеянных семян взойдут не менее трех?
Решение. Пусть событие А – из 4 семян взойдут не менее 3 семян; событие В – из 4 семян взойдут 3 семени; событие С – из 4 семян взойдут 4 семени. По теореме сложения вероятностей
 .
.
Вероятности  и
и  определим по формуле Бернулли, применяемой в следующем случае. Пусть проводится серия п независимых испытаний, при каждом из которых вероятность наступления события постоянна и равна р, а вероятность ненаступления этого события равна
определим по формуле Бернулли, применяемой в следующем случае. Пусть проводится серия п независимых испытаний, при каждом из которых вероятность наступления события постоянна и равна р, а вероятность ненаступления этого события равна  . Тогда вероятность того, что событие А в п испытаниях появится ровно
. Тогда вероятность того, что событие А в п испытаниях появится ровно  раз, вычисляется по формуле Бернулли
раз, вычисляется по формуле Бернулли
 ,
,
где  – число сочетаний из п элементов по
– число сочетаний из п элементов по  . Тогда
. Тогда

Искомая вероятность
 .
.
Задача 2. Вероятность всхожести семян пшеницы равна 0,9. Найти вероятность того, что из 400 посеянных семян взойдут 350 семян.
Решение. Вычислить искомую вероятность  по формуле Бернулли затруднительно из-за громоздкости вычислений. Поэтому применим приближенную формулу, выражающую локальную теорему Лапласа:
по формуле Бернулли затруднительно из-за громоздкости вычислений. Поэтому применим приближенную формулу, выражающую локальную теорему Лапласа:
 ,
,
где  и
и  .
.
Из условия задачи  . Тогда
. Тогда
 .
.
Из таблицы 1 приложений находим 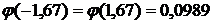 . Искомая вероятность равна
. Искомая вероятность равна
 .
.
Задача 3. Среди семян пшеницы 0,02% сорняков. Какова вероятность того, что при случайном отборе 10000 семян будет обнаружено 6 семян сорняков?
Решение. Применение локальной теоремы Лапласа из-за малой вероятности  приводит к значительному отклонению вероятности от точного значения
приводит к значительному отклонению вероятности от точного значения  . Поэтому при малых значениях р для вычисления
. Поэтому при малых значениях р для вычисления  применяют асимптотическую формулу Пуассона
применяют асимптотическую формулу Пуассона
 , где
, где  .
.
Эта формула используется при 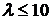 , причем чем меньше р и больше п, тем результат точнее.
, причем чем меньше р и больше п, тем результат точнее.
По условию задачи  ;
;  . Тогда
. Тогда
 и
и
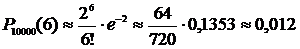 .
.
Задача 4. Процент всхожести семян пшеницы равен 90%. Найти вероятность того, что из 500 посеянных семян взойдут от 400 до 440 семян.
Решение. Если вероятность наступления события А в каждом из п испытаний постоянна и равна р, то вероятность  того, что событие А в таких испытаниях наступит не менее
того, что событие А в таких испытаниях наступит не менее  раз и не более
раз и не более  раз определяется по интегральной теореме Лапласа следующей формулой:
раз определяется по интегральной теореме Лапласа следующей формулой:
 , где
, где
 ,
,  .
.
Функция  называется функцией Лапласа. В приложениях (табл. 2) даны значения этой функции для
называется функцией Лапласа. В приложениях (табл. 2) даны значения этой функции для  . При
. При  функция
функция  . При отрицательных значениях х в силу нечетности функции Лапласа
. При отрицательных значениях х в силу нечетности функции Лапласа  . Используя функцию Лапласа, имеем:
. Используя функцию Лапласа, имеем:
 .
.
По условию задачи  . По приведенным выше формулам находим
. По приведенным выше формулам находим  и
и 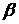 :
:
 .
.
Тогда
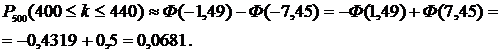
Задача 5. Задан закон распределения дискретной случайной величины Х:

Найти: 1) математическое ожидание  ; 2) дисперсию
; 2) дисперсию  ; 3) среднее квадратическое отклонение
; 3) среднее квадратическое отклонение  .
.
Решение. 1) Если закон распределения дискретной случайной величины задан таблицей

где в первой строке даны значения случайной величины Х, а во второй – вероятности этих значений, то математическое ожидание  вычисляется по формуле
вычисляется по формуле
 .
.
Тогда  .
.
2) Дисперсия  дискретной случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е.
дискретной случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е.
 .
.
Эта величина характеризует среднее ожидаемое значение квадрата отклонения Х от  . Из последней формулы имеем
. Из последней формулы имеем

Дисперсию  можно найти другим способом, исходя из следующего ее свойства: дисперсия
можно найти другим способом, исходя из следующего ее свойства: дисперсия  равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания
равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания  , то есть
, то есть
 .
.
Для вычисления  составим следующий закон распределения величины
составим следующий закон распределения величины  :
:

Тогда

3) Для характеристики рассеяния возможных значений случайной величины вокруг ее среднего значения вводится среднее квадратическое отклонение  случайной величины Х, равное квадратному корню из дисперсии
случайной величины Х, равное квадратному корню из дисперсии  , то есть
, то есть
 .
.
Из этой формулы имеем: 
Задача 6. Непрерывная случайная величина Х задана интегральной функцией распределения

Найти: 1) дифференциальную функцию распределения  ; 2) математическое ожидание
; 2) математическое ожидание  ; 3) дисперсию
; 3) дисперсию  .
.
Решение. 1) Дифференциальной функцией распределения  непрерывной случайной величины Х называется производная от интегральной функции распределения
непрерывной случайной величины Х называется производная от интегральной функции распределения  , то есть
, то есть
 .
.
Искомая дифференциальная функция имеет следующий вид:

2) Если непрерывная случайная величина Х задана функцией  , то ее математическое ожидание определяется формулой
, то ее математическое ожидание определяется формулой

Так как функция  при
при  и при
и при  равна нулю, то из последней формулы имеем
равна нулю, то из последней формулы имеем
 .
.
3) Дисперсию  определим по формуле
определим по формуле

Тогда

Задача 7. Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 40 мм и средним квадратическим отклонением 3 мм. Найти: 1) вероятность того, что длина произвольно взятой детали будет больше 34 мм и меньше 43 мм; 2) вероятность того, что длина детали отклонится от ее математического ожидания не более чем на 1,5 мм.
Решение. 1) Пусть Х – длина детали. Если случайная величина Х задана дифференциальной функцией  , то вероятность того, что Х примет значения, принадлежащие отрезку
, то вероятность того, что Х примет значения, принадлежащие отрезку  , определяется по формуле
, определяется по формуле
 .
.
Вероятность выполнения строгих неравенств 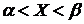 определяется той же формулой. Если случайная величина Х распределена по нормальному закону, то
определяется той же формулой. Если случайная величина Х распределена по нормальному закону, то
 , (1)
, (1)
где  – функция Лапласа,
– функция Лапласа,  .
.
В задаче  . Тогда
. Тогда

2) По условию задачи  , где
, где  . Подставив в (1)
. Подставив в (1)  , имеем
, имеем

то есть
 . (2)
. (2)
Из формулы (2) имеем:
 .
.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
СПРАВОЧНЫЕ ФОРМУЛЫ
СОБЫТИЯ А, В, С …
| Сумма событий (хотя бы или А, или В) | А + В | 
  А В А В
|
| Произведение событий (и А, и В одновременно) | А × В |     
 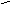 А В А В
|
| Виды событий | Обозначение или определение | |
| Невозможное | V – заведомо не произойдет | |
| Достоверное (истинное) | U – обязательно произойдет | |
| Случайное | в результате испытания может либо произойти, либо не произойти | |
| Несовместные А и В | если появление А исключает появление В, т. е. А × В= V | |
| Совместные А и В | если появление А не исключает появление В, т. е. А × В¹ V | |
| Равновозможные А и В | если ни одно из них не является более возможным, чем другое | |
Противоположные А и 
| если 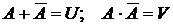
| |
| Полная группа А 1, А 2,… Аk | если 
| |
| Независимые А и В | если А не зависит от В и наоборот |
СОЕДИНЕНИЯ
| РАЗМЕЩЕНИЯ – группы элементов, отличающиеся друг от друга и элементами, и порядком | 
|
| ПЕРЕСТАНОВКИ – группы элементов, отличающиеся друг от друга только порядком элементов. | 
|
| СОЧЕТАНИЯ – группы элементов, отличающиеся друг от друга только самими элементами | 
|
ОТНОСИТЕЛЬНАЯ ЧАСТОТА события А  п – общее число испытаний
m – число появлений события А
п – общее число испытаний
m – число появлений события А
| ВЕРОЯТНОСТЬ события А
 п – общее число всех равновозможных несовместных элементарных исходов, образующих полную группу
m – число исходов, благоприятствующих событию А
п – общее число всех равновозможных несовместных элементарных исходов, образующих полную группу
m – число исходов, благоприятствующих событию А
| |||
ЗАКОН БОЛЬШИХ ЧИСЕЛ БЕРНУЛЛИ при 
| ||||
| СВОЙСТВА ВЕРОЯТНОСТИ | 
| 
| 
| |
СЛОЖЕНИЕ: Если А и В - несовместны, то
 Если А и В - совместны, то Если А и В - совместны, то 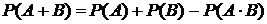
| ПРОИЗВЕДЕНИЕ: Если А и В - независимы, то
 Если А и В - зависимы, то
Если А и В - зависимы, то  Условной вероятностью РА называют вероятность события В, вычисленную в предположении, что событие А уже произошло.
Условной вероятностью РА называют вероятность события В, вычисленную в предположении, что событие А уже произошло.
| |||
Следствия: 1. Если А и  - противоположные события, то - противоположные события, то  или или  .
2. Вероятность появления хотя бы одного события из А 1, А 2,… Аk: .
2. Вероятность появления хотя бы одного события из А 1, А 2,… Аk: 
| ||||
ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ: А происходит с одной из гипотез Нi. Если Н1+Н2+…+Нп=U; Hi×Hj=V; i¹j, то 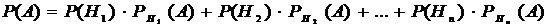
| ||||
ФОРМУЛА БЕЙЕСА позволяет найти изменение вероятности гипотез, если событие А произошло.
 , где Р(А) – полная вероятность. , где Р(А) – полная вероятность.
| ||||
ПОВТОРЕНИЕ ИСПЫТАНИЙ
Производится п испытаний (независимых), вероятность каждого  , а , а  . Находим вероятность того, что событие А появилось ровно т раз. . Находим вероятность того, что событие А появилось ровно т раз.
| ||||||||||||||||||||||
ФОРМУЛА БЕРНУЛЛИ (п – мало)

| ЛОКАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА (п – велико)
 , где , где 
| |||||||||||||||||||||
ФОРМУЛА ПУАССОНА (р – мало, п – велико)
 , , 
| ИНТЕГРАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА

 ; ; 
| |||||||||||||||||||||
Вероятность появления хотя бы одного события в п испытаниях:  . .
| ||||||||||||||||||||||
Примечание:
 - четная функция, т.е. - четная функция, т.е.  . Ее значения находят из таблицы, . Ее значения находят из таблицы,  . .
|
 - нечетная функция, т.е. - нечетная функция, т.е.  . Функцию Ф(х) часто называют функцией Лапласа. Ее значения находят из таблицы, причем при х >5 . Функцию Ф(х) часто называют функцией Лапласа. Ее значения находят из таблицы, причем при х >5  . .
| |||||||||||||||||||||
 у у

х
- s 0 s а= 0 s =1 |  у
0,5
у
0,5
у=Ф(х)
-0,5
| |||||||||||||||||||||
Отклонение W(A) от постоянной вероятности в независимых испытаниях
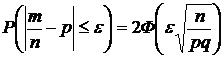
|
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
| Случайная величины – это величина, которая в результате опыта со случайным исходом принимает то или иное значение. Х – случайная величина, х – ее возможное значение. | ||||||||||||||||||||||||||
| ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА – это случайная величина, у которой множество возможных значений конечно или счетно (т.е. их можно перенумеровать в каком-то порядке). | НЕПРЕРВЫНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА – это случайная величина, у которой множество возможных значений сплошь занимает какой-то участок числовой оси, границы которого могут быть как зафиксированными, так и неопределенными. | |||||||||||||||||||||||||
| ЗАКОН РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ– это всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующим им вероятностям (для дискретной случайной величины) или плотностями вероятностей (для непрерывной случайной величины). | ||||||||||||||||||||||||||
р1+р2+ …+рп +…=1 рп - вероятности
Многоугольник распределения |  , где f(x) – плотность распределения , где f(x) – плотность распределения
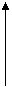 вероятностей Х. вероятностей Х.
  f(x) Ее свойства: f(x) Ее свойства:
 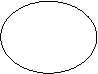 1. 1. 
 График плотности 2. График плотности 2.  распределения 3. распределения 3. 
| |||||||||||||||||||||||||
ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ–
это вероятность того, что случайная величина примет значение меньшее, чем заданное х, т.е.
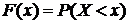
| ||||||||||||||||||||||||||
| Функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. | Свойства:
1. F(x) – неубывающая функция
2. F (-¥)=0
3. F (+¥)=1
4. 0£ F(x) £1
5.  6.
6. 
| Функция распределения любой непрерывной случайной величины есть непрерывная функция в любой точке и дифференцируема всюду.
Вероятность любого отдельного значения непрерывной случайной величины равна нулю, т.е.  .
Связь между плотностью и функцией распределения непрерывной случайной величины .
Связь между плотностью и функцией распределения непрерывной случайной величины 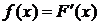 . .
| ||||||||||||||||||||||||

|         F(x) F(x)
  р1+р2 р1+р2
 р1
х1 0 х2 х3 …хп х р1
х1 0 х2 х3 …хп х
|        F(x) 1
0 х F(x) 1
0 х

| ||||||||||||||||||||||||
| ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН | ||||||||||||||||||||||||||
Дискретная случайная величина

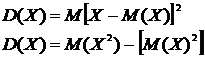
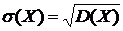
| МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДИСПЕРСИЯ СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ | Непрерывная случайная величина
 × ×

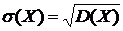
| ||||||||||||||||||||||||
| Свойства: М(С)=С D(С)=0 М(СХ)=С×М(Х) D(CX)=C2×D(X) М(Х±Y)=М(Х)±М(Y) D(Х±Y)=D(Х)+D(Y) М(Х×Y)=М(Х)×М(Y) | ||||||||||||||||||||||||||
| ВИДЫРАСПРЕДЕЛЕНИЙ СЛУЧАЙНЫХ ВЕЛИЧИН | ||||||||||||||||||||||||||
Дискретная случайная величина
БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
М(Х)=пр; D(Х)=прq; q=1-p
РАСПРЕДЕЛЕНИЕ ПУАССОНА М(Х)=l; D(Х)=l; l=пр £10; р- мало; п -велико
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2017-12-29 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд Интересно: |










 0 х
0 х







 или
или  р2 р
р2 р






 х1 х2 хп
х1 х2 хп