Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Саратовский государственный технический университет имени Гагарина Ю.А.»
Кафедра «Математика и моделирование»
ПРИЛОЖЕНИЕ ИНТЕГРАЛОВ И ТЕОРИИ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Методические указания и задания
К выполнению расчетно-графической работы
По дисциплине «Математика»
Для студентов автомеханического факультета
Одобрено
Редакционно-издательским советом
СГТУ имени Гагарина Ю.А.
Саратов 2014
ВВЕДЕНИЕ
Современная подготовка бакалавра и специалиста требует от него не только знания специальных дисциплин, но и умения формулировать возникающие задачи в математической форме. Задачи, включенные в данные методические указания, касаются двух больших разделов математического анализа: применение теории определенных интегралов к решению геометрических и физических задач, а также исследование экстремальных задач функции многих переменных.
Целью методических указаний является оказание практической помощи студентам при выполнении расчетно-графической работы (РГР) по данным разделам математики.
Расчетно-графическая работа является одной из форм самостоятельной работы студентов, способствующей активизации учебного процесса, улучшению познавательной деятельности студентов, выработке у них способности самостоятельно решать сложные проблемы.
Расчетно-графическая работасодержит шесть заданий. Необходимый теоретический материал изучается студентами в курсе лекций по дисциплине «Математика», поэтому в методических указаниях приводится ограниченное число теоретических сведений по каждому разделу. В конце методических указаний разбирается также решение ряда типовых примеров и приводится список основной литературы, которая имеется в научной библиотеке университета и окажется полезной при выполнении РГР.
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ И ЗАЩИТЕ
РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ
Выполнение расчетно-графической работы производится в соответствии с учебным планом специальности по графику, установленному кафедрой. Номер варианта указывает студенту преподаватель.
Прежде чем приступить к решению задач, студент должен изучить теоретический материал по указанной литературе.
После этого студент должен в письменной форме в отдельной тетради с титульным листом представить решения задач соответствующего варианта. Перед решением записывается полностью условие задачи. В процессе решения приводятся необходимые формулы и литература. Решение должно быть подробным и аккуратно оформленным.
Контроль выполнения расчетно-графической работы производится в два этапа:
1) предварительная проверка преподавателем решения заданий;
2) защита расчетно-графической работы перед группой.
Во время защиты студент должен уметь отвечать на теоретические вопросы, пояснять решения заданий работы.
Студенты, не предъявившие расчетно-графическую работу на предварительную проверку, к защите не допускаются.
ПРИМЕНЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Задание 1.
При выполнении задания необходимо предварительно построить в соответствующей системе координат кривые или фигуры, ограниченные указанными линиями.
1.1. Вычислить площадь фигуры, ограниченной линиями 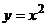 ; ;  . .
|
1.2. Вычислить длину дуги кривой  , заключенной внутри окружности , заключенной внутри окружности  . .
|
1.3. Вычислить площадь фигуры, ограниченной астроидой  ; ; 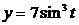 . .
|
1.4. Вычислить площадь фигуры, ограниченной линиями  ; ;  . .
|
1.5. Вычислить площадь фигуры, ограниченной кардиоидой  . .
|
1.6. Вычислить длину дуги кривой  , отсеченной прямой , отсеченной прямой  . .
|
1.7. Вычислить площадь фигуры, ограниченной линиями  ; ;  . .
|
1.8. Вычислить длину дуги кривой  при при  . .
|
1.9. Вычислить площадь фигуры, ограниченной первой аркой циклоиды  и прямой и прямой  при при  . .
|
1.10. Вычислить длину дуги кривой  , отсеченной прямой , отсеченной прямой  . .
|
1.11. Вычислить площадь фигуры, ограниченной «трехлепестковой розой»  . .
|
1.12. Вычислить длину кривой  , находящейся внутри окружности , находящейся внутри окружности  . .
|
1.13. Вычислить площадь фигуры, ограниченной линиями  . .  . .
|
1.14. Вычислить длину дуги кардиоиды  . .
|
1.15. Вычислить площадь фигуры, ограниченной эллипсом  , ,  . .
|
1.16. Вычислить длину дуги кривой  от от  до до  . .
|
1.17. Вычислить площадь фигуры, ограниченной лемнискатой Бернулли  . .
|
1.18. Вычислить длину дуги одной арки циклоиды  при при  . .
|
1.19. Вычислить площадь фигуры, ограниченной линиями  ; ;  . .
|
1.20. Вычислить площадь фигуры, ограниченной «восьмилепестковой розой»  . .
|
1.21. Вычислить площадь фигуры, ограниченной линиями  , ,  и и  . .
|
1.22. Вычислить длину дуги от вершины параболы  до точки с абсциссой до точки с абсциссой  . .
|
1.23. Вычислить площадь фигуры, ограниченной лемнискатой Бернулли  . .
|
1.24. Вычислить длину дуги кривой  от от  до до  . .
|
1.25. Вычислить площадь фигуры, ограниченной линиями  ; ;  ; ;  . .
|
1.26. Вычислить площадь фигуры, ограниченной локоном Аньези  и прямой и прямой  . .
|
1.27. Вычислить площадь фигуры, ограниченной линиями  ; ;  . .
|
1.28. Вычислить площадь фигуры, ограниченной одним лепестком «четырехлепестковой розы»  . .
|
1.29. Вычислить площадь фигуры, ограниченной линиями  ; ;  . .
|
1.30. Вычислить площадь фигуры, ограниченной «двухлепестковой розой»  . .
|
Задание 2.
При выполнении задания необходимо предварительно построить в соответствующей системе координат тело вращения. При вычислении объема тела по известным площадям поперечных сечений для построения тела использовать метод сечений. Площадь эллипса принять равной  .
.
2.1. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной линиями фигуры, ограниченной линиями  ; ;  . .
|
2.2. Вычислить объем тела, ограниченного поверхностями  , ,  , ,  . .
|
2.3. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной линиями фигуры, ограниченной линиями  ; ;  . .
|
2.4. Вычислить объем тела, ограниченного параболоидом  и плоскостью и плоскостью  . .
|
2.5. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной линиями фигуры, ограниченной линиями  ; ;  ; ;  . .
|
2.6. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной одной аркой циклоиды фигуры, ограниченной одной аркой циклоиды  . .
|
2.7. Вычислить объем тела, ограниченного эллипсоидом  . .
|
2.8. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной линиями фигуры, ограниченной линиями  ; ;  . .
|
2.9. Вычислить объем тела, ограниченного поверхностями  , , 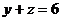 , ,  . .
|
2.10. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной линиями фигуры, ограниченной линиями  ; ;  ; ;  . .
|
2.11. Вычислить объем тела, ограниченного параболическим цилиндром  , плоскостями , плоскостями  , ,  , ,  , ,  . .
|
2.12. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной эллипсом фигуры, ограниченной эллипсом  . .
|
2.13. Вычислить объем шарового слоя, вырезанного из шара  плоскостями плоскостями  и и  . .
|
2.14. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной линиями фигуры, ограниченной линиями  ; ;  ; ;  ; ;  . .
|
2.15. Вычислить объем тела, ограниченного однополостным гиперболоидом  , и плоскостями , и плоскостями  , ,  . .
|
2.16. Вычислить объем тела, полученного вращением вокруг полярной оси кардиоиды  . .
|
2.17. Вычислить объем тела, ограниченного параболическим цилиндром  , плоскостями , плоскостями  , ,  , ,  . .
|
2.18. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной линиями фигуры, ограниченной линиями  ; ;  , ,  . .
|
2.19. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной астроидой фигуры, ограниченной астроидой  ; ;  . .
|
2.20. Вычислить объем тела, ограниченного конической поверхностью  и плоскостью и плоскостью  . .
|
2.21. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной линией фигуры, ограниченной линией  . .
|
2.22. Вычислить объем тела, полученного вращением кривой  вокруг полярной оси. вокруг полярной оси.
|
2.23. Вычислить объем тела, ограниченного эллиптическим параболоидом  и плоскостью и плоскостью  . .
|
2.24. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной линиями фигуры, ограниченной линиями  ; ;  ; ;  . .
|
2.25. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной линиями фигуры, ограниченной линиями  ; ;  . .
|
2.26. Цилиндр, основанием которого служит эллипс  , пересечен наклонной плоскостью, проходящей через малую ось эллипса. Высота полученного «цилиндрического клина» равна 5. Построить тело и вычислить его объем. , пересечен наклонной плоскостью, проходящей через малую ось эллипса. Высота полученного «цилиндрического клина» равна 5. Построить тело и вычислить его объем.
|
2.27. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной линией фигуры, ограниченной линией  . .
|
2.28. Вычислить объем шарового сегмента высотой 2, отсеченного от шара, ограниченного сферической поверхностью  . .
|
2.29. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной линиями фигуры, ограниченной линиями  ; ;  . .
|
2.30. Вычислить объем тела, полученного вращением вокруг оси  фигуры, ограниченной линиями фигуры, ограниченной линиями  ; ;  . .
|
Задание 3.
При выполнении задания необходимо предварительно изобразить в системе координат заданный резервуар или сооружение. Принять удельный вес бензина  , удельные веса материалов
, удельные веса материалов  ,
,  ,
,  , число
, число  . Результат округлить до целого числа.
. Результат округлить до целого числа.
3.1. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную четырехугольную пирамиду, обращенную вершиной вниз, со стороной основания 2 м и высотой 5 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную четырехугольную пирамиду, обращенную вершиной вниз, со стороной основания 2 м и высотой 5 м.
|
3.2. Вычислить работу  , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом  , представляющего собой правильную четырехугольную усеченную пирамиду, сторона верхнего основания которой равна 2 м, нижнего – 4 м, высота - 2 м. , представляющего собой правильную четырехугольную усеченную пирамиду, сторона верхнего основания которой равна 2 м, нижнего – 4 м, высота - 2 м.
|
3.3. Вычислить работу  , которую необходимо затратить на выкачивание бензина из котла, имеющего форму сферического сегмента, высота которого , которую необходимо затратить на выкачивание бензина из котла, имеющего форму сферического сегмента, высота которого  м и радиус 1 м. м и радиус 1 м.
|
3.4. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой усеченный конус, у которого радиус верхнего основания равен 1 м, нижнего – 2 м, высота – 3 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой усеченный конус, у которого радиус верхнего основания равен 1 м, нижнего – 2 м, высота – 3 м.
|
3.5. Вычислить работу  , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом  , представляющего собой правильную шестиугольную пирамиду со стороной основания 1 м и высотой 2 м. , представляющего собой правильную шестиугольную пирамиду со стороной основания 1 м и высотой 2 м.
|
3.6. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой желоб, перпендикулярное сечение которого является параболой, длина желоба 5 м, ширина – 4 м, глубина - 4 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой желоб, перпендикулярное сечение которого является параболой, длина желоба 5 м, ширина – 4 м, глубина - 4 м.
|
3.7. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой железнодорожную цилиндрическую цистерну, радиус основания которой 1 м, длина 5 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой железнодорожную цилиндрическую цистерну, радиус основания которой 1 м, длина 5 м.
|
3.8. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную треугольную пирамиду, обращенную вершиной вниз, с основанием 2 м, высотой – 5 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную треугольную пирамиду, обращенную вершиной вниз, с основанием 2 м, высотой – 5 м.
|
3.9. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой полуцилиндрический желоб, радиус основания которого 1 м, длина – 5 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой полуцилиндрический желоб, радиус основания которого 1 м, длина – 5 м.
|
3.10. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой конус, обращенный вершиной вниз, радиус основания которого 3 м, высота 5 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой конус, обращенный вершиной вниз, радиус основания которого 3 м, высота 5 м.
|
3.11. Вычислить работу  , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом  , представляющего собой правильную четырехугольную пирамиду со стороной основания 2 м и высотой 4 м. , представляющего собой правильную четырехугольную пирамиду со стороной основания 2 м и высотой 4 м.
|
3.12. Вычислить работу  , которую необходимо затратить на выкачивание бензи-на из резервуара, представляющего собой железнодорожную цистерну в виде эллиптического цилиндра с полуосями основания 2 м и 3 м и высотой 5 м. , которую необходимо затратить на выкачивание бензи-на из резервуара, представляющего собой железнодорожную цистерну в виде эллиптического цилиндра с полуосями основания 2 м и 3 м и высотой 5 м.
|
3.13. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой параболоид вращения, радиус основания которого 2 м, глубина – 4 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой параболоид вращения, радиус основания которого 2 м, глубина – 4 м.
|
3.14. Вычислить работу  , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом  , представляющего собой правильную шестиугольную усеченную пирамиду, сторона верхнего основания которой равна 1 м, нижнего – 2 м, высота - 2 м. , представляющего собой правильную шестиугольную усеченную пирамиду, сторона верхнего основания которой равна 1 м, нижнего – 2 м, высота - 2 м.
|
3.15. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой половину эллипсоида вращения, радиус основания которого 1 м, глубина – 2 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой половину эллипсоида вращения, радиус основания которого 1 м, глубина – 2 м.
|
3.16. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой четырехугольную усеченную пирамиду, у которой сторона верхнего основания равна 2 м, нижнего – 4 м, высота – 1 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой четырехугольную усеченную пирамиду, у которой сторона верхнего основания равна 2 м, нижнего – 4 м, высота – 1 м.
|
3.17. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную шестиугольную пирамиду, обращенную вершиной вниз, со стороной основания 1 м и высотой 2 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную шестиугольную пирамиду, обращенную вершиной вниз, со стороной основания 1 м и высотой 2 м.
|
3.18. Вычислить работу  , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом  , представляющего собой конус, радиус основания которого 2 м, высота 3 м. , представляющего собой конус, радиус основания которого 2 м, высота 3 м.
|
3.19. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой цилиндрическую вертикальную цистерну с радиусом основания 1м и высотой 3м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой цилиндрическую вертикальную цистерну с радиусом основания 1м и высотой 3м.
|
3.20. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную усеченную шестиугольную пирамиду, у которой сторона верхнего основания равна 1 м, нижнего – 2 м, высота – 2 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную усеченную шестиугольную пирамиду, у которой сторона верхнего основания равна 1 м, нижнего – 2 м, высота – 2 м.
|
3.21. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой желоб, в перпендикулярном сечении которого лежит полуокружность радиусом 1 м, длина желоба 10 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой желоб, в перпендикулярном сечении которого лежит полуокружность радиусом 1 м, длина желоба 10 м.
|
3.22. Вычислить работу  , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом  , представляющего собой правильную треугольную пирамиду со стороной основания 3 м и высотой 6 м. , представляющего собой правильную треугольную пирамиду со стороной основания 3 м и высотой 6 м.
|
3.23. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой полусферу радиусом 2 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой полусферу радиусом 2 м.
|
3.24. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой нижнюю часть эллипти-ческого конуса с полуосями 3 м и 4 м, высота 6 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой нижнюю часть эллипти-ческого конуса с полуосями 3 м и 4 м, высота 6 м.
|
3.25. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную треугольную пирамиду, обращенную вершиной вниз, сторона основания которой 4 м, высота 6 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную треугольную пирамиду, обращенную вершиной вниз, сторона основания которой 4 м, высота 6 м.
|
3.26. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой усеченный конус, у которого радиус верхнего основания равен 3 м, нижнего – 1 м, высота – 3 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой усеченный конус, у которого радиус верхнего основания равен 3 м, нижнего – 1 м, высота – 3 м.
|
3.27. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную четырехугольную усеченную пирамиду, у которой сторона верхнего основания 8 м, нижнего – 4 м, высота – 2 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную четырехугольную усеченную пирамиду, у которой сторона верхнего основания 8 м, нижнего – 4 м, высота – 2 м.
|
3.28. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную треугольную усеченную пирамиду со стороной верхнего основания 2 м, нижнего основания 3 м и высотой 6 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную треугольную усеченную пирамиду со стороной верхнего основания 2 м, нижнего основания 3 м и высотой 6 м.
|
3.29. Вычислить работу  , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную усеченную шестиугольную пирамиду, у которой сторона верхнего основания равна 2 м, нижнего – 1 м, высота – 2 м. , которую необходимо затратить на выкачивание бензина из резервуара, представляющего собой правильную усеченную шестиугольную пирамиду, у которой сторона верхнего основания равна 2 м, нижнего – 1 м, высота – 2 м.
|
3.30. Вычислить работу  , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом , затрачиваемую на преодоление силы тяжести при построении сооружения из материала с удельным весом  , представляющего собой усеченный конус, радиус верхнего основания которого равен 1 м, нижнего – 2 м, высота – 2 м. , представляющего собой усеченный конус, радиус верхнего основания которого равен 1 м, нижнего – 2 м, высота – 2 м.
|
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ
МНОГИХ ПЕРЕМЕННЫХ
Задание 4.
Исследовать на экстремум следующие функции:
4.1  . .
| 4.2  . .
|
4.3  . .
| 4.4  . .
|
4.5  . .
| 4.6  . .
|
4.7 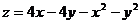 . .
| 4.8  . .
|
4.9  . .
| 4.10  . .
|
4.11 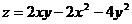 . .
| 4.12  . .
|
4.13  . .
| 4.14  . .
|
4.15  . .
| 4.16  . .
|
4.17  . .
| 4.18  . .
|
4.19  . .
| 4.20  . .
|
4.21  . .
| 4.22 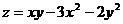 . .
|
4.23  . .
| 4.24  . .
|
4.25  . .
| 4.26  . .
|
4.27  . .
| 4.28  . .
|
4.29  . .
| 4.30 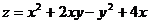 . .
|
Задание 5.
Найти наибольшее и наименьшее значения функции  в области
в области  , ограниченной заданными линиями:
, ограниченной заданными линиями:
5.1  . .
|
5.2  . .
|
5.3  . .
|
5.4  . .
|
5.5  . .
|
5.6  . .
|
5.7  . .
|
5.8  . .
|
5.9  . .
|
5.10  . .
|
5.11  . .
|
5.12  . .
|
5.13  . .
|
5.14  . .
|
5.15  . .
|
5.16  . .
|
5.17  . .
|
5.18  . .
|
5.19  . .
|
5.20  . .
|
5.21  . .
|
5.22  . .
|
5.23  . .
|
5.24 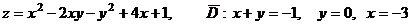 . .
|
5.25  . .
|
5.26  . .
|
5.27  . .
|
5.28  . .
|
5.29  . .
|
5.30  . .
|
Задание 6.
Найти условные экстремумы функций методом множителей Лагранжа:
6.1  при ограничении при ограничении  . .
|
6.2 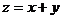 при ограничении при ограничении  . .
|
6.3  при ограничении при ограничении  . .
|
6.4  при ограничении при ограничении  . .
|
6.5  при ограничении при ограничении  . .
|
6.6  при ограничении при ограничении  . .
|
6.7  при ограничении при ограничении  . .
|
6.8  при ограничении при ограничении  . .
|
6.9  при ограничении при ограничении  . .
|
6.10  при ограничении при ограничении  . .
|
6.11  при ограничении при ограничении  . .
|
6.12  при ограничении при ограничении  . .
|
6.13  при ограничении при ограничении  . .
|
6.14  при ограничении при ограничении 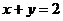 . .
|
6.15 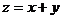 при ограничении при ограничении  . .
|
6.16  при ограничении при ограничении  . .
|
6.17  при ограничении при ограничении  . .
|
6.18  при ограничении при ограничении  . .
|
6.19  при ограничении при ограничении  . .
|
6.20  при ограничении при ограничении  . .
|
6.21  при ограничении при ограничении  . .
|
6.22  при ограничении при ограничении  . .
|
6.23  при ограничении при ограничении  . .
|
6.24  при ограничении при ограничении  . .
|
6.25  при ограничении при ограничении  . .
|
6.26  при ограничении при ограничении  . .
|
6.27  при ограничении при ограничении  . .
|
6.28  при ограничении при ограничении  . .
|
6.29  при ограничении при ограничении  . .
|
6.30  при ограничении при ограничении  . .
|
Решения типовых задач
Площади плоских фигур
Вычисление площадей плоских фигур основано на геометрическом смысле определенного интеграла.
1.1 Площадь криволинейной трапеции, ограниченной сверху графиком функции  , слева и справасоответственно прямыми
, слева и справасоответственно прямыми  и
и  , снизу – отрезком
, снизу – отрезком  оси
оси  (см. рис. 1),
(см. рис. 1),

Рис. 1
вычисляется по формуле
 . .
| (1) |
Если  при
при  , то
, то
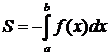 . .
| (2) |
Площадь фигуры, ограниченной кривыми  и
и  , причем
, причем  , прямыми
, прямыми  и
и  (см. рис. 2),
(см. рис. 2),

Рис. 2
вычисляется по формуле
 . .
| (3) |
Если криволинейная трапеция ограничена кривой  , прямыми
, прямыми  и
и  и отрезком
и отрезком  оси
оси  , тогда площадь этой трапеции вычисляется по формуле
, тогда площадь этой трапеции вычисляется по формуле
 . .
| (4) |
Пример 1. Найти площадь фигуры, ограниченной линиями  и
и  .
.
Решение. Найдем абсциссы точек пересечения графиков данных функций. Для этого решаем систему уравнений

Отсюда находим  .
.

Рис. 3
Искомую площадь (см. рис. 3) находим по формуле (3):
 . 3
. 3
1.2. Если криволинейная трапеция ограничена сверху кривой, заданной параметрическими уравнениями 
 ,
,  , прямыми
, прямыми  и
и  и отрезком
и отрезком  оси
оси  , то ее площадь вычисляется по формуле
, то ее площадь вычисляется по формуле
 , ,
| (5) |
где  и
и  определяются
определяются