Физических задач
Работа переменной силы, заданной функцией  и направлен-ной вдоль оси
и направлен-ной вдоль оси  на отрезке
на отрезке  , равна интегралу
, равна интегралу
 . .
| (15) |
Для вычисления силы давления жидкости используют «закон Паскаля»: давление жидкости на горизонтальную пластину площади  равно весу столба этой жидкости, т.е.
равно весу столба этой жидкости, т.е.  , где
, где 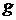 - ускорение свободного падения,
- ускорение свободного падения,  - плотность жидкости,
- плотность жидкости,  - глубина ее погружения.
- глубина ее погружения.
Пример 11. Найти работу, которую нужно затратить, чтобы выкачать воду из корыта, имеющего форму полуцилиндра, длина которого  , радиус
, радиус  (рис. 13).
(рис. 13).
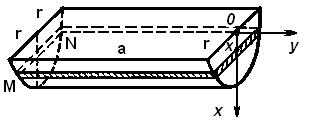
Рис. 13
Решение. Введем систему координат так как указано на рис. 13.
Работа, затрачиваемая на поднятие тела весом  на высоту
на высоту  , равна
, равна  . Однако различные слои жидкости в резервуаре находятся на различных глубинах и высота поднятия до края резервуара различных слоев не одинакова.
. Однако различные слои жидкости в резервуаре находятся на различных глубинах и высота поднятия до края резервуара различных слоев не одинакова.
Учитывая, что вес воды равен  , где
, где  - удельный вес,
- удельный вес,  - плотность воды, найдем сначала объем элементарного слоя воды, находящегося на глубине
- плотность воды, найдем сначала объем элементарного слоя воды, находящегося на глубине  и имеющего длину
и имеющего длину  , ширину
, ширину  и толщину
и толщину  :
:
 .
.
Найдем элементарную работу, совершаемую для поднятия этого слоя воды на высоту  ,:
,:
 .
.
Следовательно,

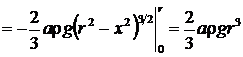 . 3
. 3
Пример 12. Какую работу надо затратить, чтобы насыпать кучу песка конической формы с радиусом основания  , высотой
, высотой 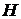 и плотностью
и плотностью
песка  .
.
Решение. 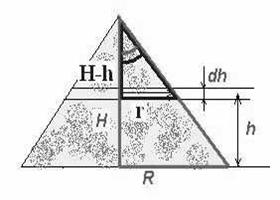 Рассмотрим физическую модель. В данном случае работа затрачивается при поднятии песка на некоторую высоту.
Рассмотрим физическую модель. В данном случае работа затрачивается при поднятии песка на некоторую высоту.
Работу можно вычислить по формуле 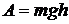 , где
, где  – масса песка,
– масса песка, 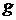 – ускорение свободного падения,
– ускорение свободного падения,  – высота, на которую поднимают песок.
– высота, на которую поднимают песок.
Однако трудность заключается в том, что разные части песка нужно поднимать на разную высоту.
Разобьем наш конус на тонкие горизонтальные пласты толщиной  . Рассмотрим один из таких пластов.
. Рассмотрим один из таких пластов.
Можно считать, что всю массу песка  такого пласта подняли на одну и ту же высоту
такого пласта подняли на одну и ту же высоту  . При этом
. При этом  и работа по поднятию этого тонкого пласта
и работа по поднятию этого тонкого пласта  .
.
Из рисунка видно, что выделенные треугольники подобны, имеют общий угол, причем
 .
.
Отсюда  . Величина
. Величина  изменяется для разных пластов от
изменяется для разных пластов от  до
до 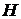 .
.
Для того, чтобы найти полную работу, нужно просуммировать элементарные работы  для всех тонких пластов. При переходе к пределу при
для всех тонких пластов. При переходе к пределу при  , суммирование превращается в интегрирование и окончательно получаем
, суммирование превращается в интегрирование и окончательно получаем
 .3
.3
5. Функции многих переменных
5.1 Определение экстремума функции двух переменных в точке.
Рассмотрим функцию  двух переменных, определенную в некоторой области
двух переменных, определенную в некоторой области  . Функция
. Функция  имеет в точке
имеет в точке  :
:
локальный максимум, если неравенство  имеет место во всех точках
имеет место во всех точках  из некоторой достаточно малой окрестности точки
из некоторой достаточно малой окрестности точки  ;
;
локальный минимум, если неравенство  имеет место во всех точках
имеет место во всех точках  из некоторой достаточно малой окрестности точки
из некоторой достаточно малой окрестности точки  .
.
Максимум или минимум функции называется ее экстремумом. Точка  , в которой функция имеет экстремум, называется точкой экстремума.
, в которой функция имеет экстремум, называется точкой экстремума.
Необходимые условия экстремума. Если дифференцируемая функция  достигает экстремума в точке
достигает экстремума в точке  , то ее частные производные первого порядка в этой точке равны нулю, т.е.
, то ее частные производные первого порядка в этой точке равны нулю, т.е.
 ,
,  .
.
Точки, в которых частные производные первого порядка равны нулю, называются стационарными точками.
Не всякая стационарная точка является точкой экстремума.
Достаточные условия экстремума. Пусть  - стационарная точка функции
- стационарная точка функции  . Обозначим
. Обозначим
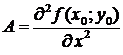 ,
,  ,
, 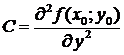
и составим дискриминант  . Тогда:
. Тогда:
если 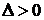 и
и  , то
, то  - точка максимума;
- точка максимума;
если 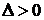 и
и  , то
, то  - точка минимума;
- точка минимума;
если  , то в точке
, то в точке  экстремума нет;
экстремума нет;
если  , то требуется дополнительное исследование.
, то требуется дополнительное исследование.
Пример 12. Исследовать на экстремум функцию  .
.
Решение. Находим частные производные первого порядка:

Воспользовавшись необходимыми условиями экстремума, находим стационарные точки: 
Решениями системы уравнений  будут точки
будут точки  ,
,  ,
, 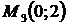 ,
,  .
.
Найденные точки являются стационарными точками данной функции.
Найдем вторые частные производные данной функции:
 .
.
Найдем значения частных производных второго порядка в каждой стационарной точке и составим дискриминант 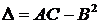 .
.
Имеем:
а) для точки  :
:
 ;
;
 .
.
Согласно достаточным условиям экстремума в точке  экстремума нет;
экстремума нет;
б) для точки  :
:
 ;
;
 , т.е. экстремума нет;
, т.е. экстремума нет;
в) для точки 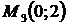 :
:
 ;
;
 , т.е. экстремума нет;
, т.е. экстремума нет;
г) для точки  :
:
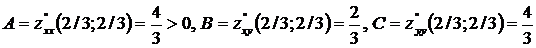
 , т.е. имеем точку локального минимума:
, т.е. имеем точку локального минимума:  . 3
. 3
5.2 Наибольшее и наименьшее значение функции в замкнутой области. Для того, чтобы найти наибольшее и наименьшее значения функции  в замкнутой области, надо:
в замкнутой области, надо:
найти стационарные точки, расположенные в данной области, и вычислить значения функции в этих точках;
найти наибольшее и наименьшее значения функции на линиях, образующих границу области;
из всех найденных значений выбрать наибольшее и наименьшее.
Пример 13. Найти наибольшее и наименьшее значения функции  в замкнутой области
в замкнутой области  , ограниченной осью
, ограниченной осью  , прямой
, прямой  и параболой
и параболой  при
при  .
. 
Решение. Изобразим область  на плоскости
на плоскости  .
.

Точки, в которых функция принимает наибольшее и наименьшее значения, могут находиться как внутри области  , так и на ее границе.
, так и на ее границе.
Если функция принимает наибольшее (наименьшее) значение во внутренней области, то в этой точке частные производные первого порядка равны нулю:  ,
,  .
.
Решив систему полученных уравнений, найдем две точки  и
и  , в которых обе частные производные равны нулю. Первая из них принадлежит границе области. Следовательно, если функция
, в которых обе частные производные равны нулю. Первая из них принадлежит границе области. Следовательно, если функция  принимает наибольшее (наименьшее) значение во внутренней точке области, то это может быть только в точке
принимает наибольшее (наименьшее) значение во внутренней точке области, то это может быть только в точке  .
.
Исследуем функцию на границе области.
На отрезке  имеем
имеем  , поэтому на этом отрезке
, поэтому на этом отрезке  - возрастающая функция одной переменной
- возрастающая функция одной переменной  . Наибольшее и наименьшее значения она принимает на концах отрезка
. Наибольшее и наименьшее значения она принимает на концах отрезка  .
.
На отрезке  имеем
имеем  , следовательно, на этом отрезке функция
, следовательно, на этом отрезке функция  , представляет собой функцию одной переменной
, представляет собой функцию одной переменной  , ее наибольшее и наименьшее значения находятся среди ее значений в критических точках и на концах отрезка. Находим производную
, ее наибольшее и наименьшее значения находятся среди ее значений в критических точках и на концах отрезка. Находим производную  . Находим критические точки:
. Находим критические точки:  .
.
Внутри отрезка  имеется лишь одна критическая точка
имеется лишь одна критическая точка  . Соответствующей точкой отрезка
. Соответствующей точкой отрезка  является точка
является точка  . Итак, наибольшее и наименьшее значения функции
. Итак, наибольшее и наименьшее значения функции  на отрезке
на отрезке  находятся среди ее значений в точках
находятся среди ее значений в точках  .
.
На дуге  параболы
параболы  имеем:
имеем:
 .
.
Найдем критические точки  .
.
Таким образом, наибольшее и наименьшее значения функции  на дуге
на дуге  находятся среди ее значений в точках
находятся среди ее значений в точках  .
.
Следовательно, наибольшее и наименьшее значения функции  в данной замкнутой области находятся среди ее значений в точках
в данной замкнутой области находятся среди ее значений в точках  , т.е. среди значений:
, т.е. среди значений:
 ;
;  ;
;  ;
;
 ;
;  ;
;  .
.
Наибольшее и наименьшее из них соответственно равны 12 и -1.
Они являются наибольшим и наименьшим значениями данной функции в замкнутой области  . 3
. 3
5.3 Условный экстремум. Условным экстремумом функции  называется экстремум этой функции, достигнутый при условии, что переменные
называется экстремум этой функции, достигнутый при условии, что переменные  и
и  связаны уравнением
связаны уравнением  (уравнение связи).
(уравнение связи).
Отыскание условного экстремума можно свести к исследованию на обычный экстремум так называемой функции Лагранжа
 ,
,
где  - неопределенный постоянный множитель Лагранжа.
- неопределенный постоянный множитель Лагранжа.
Необходимые условия экстремума функции Лагранжа имеют вид
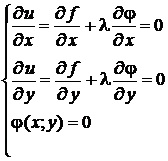 .
.
Из этой системы трех уравнений можно найти неизвестные  ,
,  и
и  .
.
Достаточные условия экстремума функции Лагранжа.
Пусть  ,
,  - стационарная точка функции
- стационарная точка функции  , тогда определитель
, тогда определитель 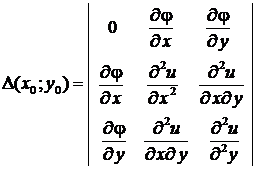 дает условия экстремума:
дает условия экстремума:
если 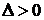 , то
, то  имеет в точке
имеет в точке  условный максимум;
условный максимум;
если  , то
, то  имеет в точке
имеет в точке  условный минимум.
условный минимум.
Геометрически задача отыскания условного экстремума сводится к нахождению экстремальных точек кривой, по которой поверхность  пересекается с цилиндром
пересекается с цилиндром  .
.
Пример 14. Найти экстремум функции  при условии, что
при условии, что  и
и  связаны уравнением
связаны уравнением 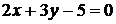 .
.
Решение. Рассмотрим функцию Лагранжа  .
.
Имеем  ,
,  . Из системы уравнений (необходимые условия экстремума)
. Из системы уравнений (необходимые условия экстремума)  находим
находим 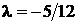 ,
,  ,
,  .
.
В нашем случае получаем в точке 
 ,
,
т. е. в этой точке функция  принимает условный максимум
принимает условный максимум  .3
.3