Лекция 4
Термин "морфизм" в математике - это полный (или почти полный) синоним термина "отображение" (множеств).
Линейное пространство
Определения
Пусть дано множество 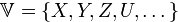 элементов произвольной природы. Пусть для элементов этого множества определены две операции: сложения
элементов произвольной природы. Пусть для элементов этого множества определены две операции: сложения 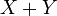 и умножения на любое вещественное число
и умножения на любое вещественное число  :
:  , и множество
, и множество 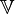 замкнуто относительно этих операций:
замкнуто относительно этих операций: 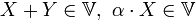 . Пусть эти операции подчиняются аксиомам:
. Пусть эти операции подчиняются аксиомам:
1. 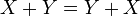 для
для 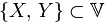 ;
;
2. 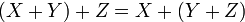 для
для 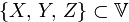 ;
;
3. в 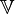 cуществует нулевой вектор
cуществует нулевой вектор 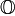 со свойством
со свойством 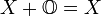 для
для 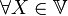 ;
;
4. для каждого 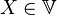 существует обратный вектор
существует обратный вектор 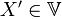 со свойством
со свойством  ;
;
5. 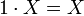 для
для 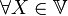 ;
;
6.  для
для 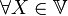 ,
, 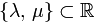 ;
;
7. 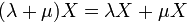 для
для 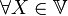 ,
, 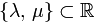 ;
;
8. 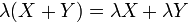 для
для 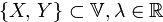 .
.
Тогда такое множество 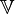 называется линейным (векторным) пространством, его элементы называются векторами, и — чтобы подчеркнуть их отличие от чисел из
называется линейным (векторным) пространством, его элементы называются векторами, и — чтобы подчеркнуть их отличие от чисел из  — после
— после
Изоморфизм линейных пространств
Говорят, что между элементами двух множеств 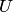 и
и 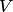 установлено взаимно однозначное соответствие, если указано правило, которое каждому элементу
установлено взаимно однозначное соответствие, если указано правило, которое каждому элементу 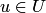 сопоставляет один и только один элемент
сопоставляет один и только один элемент 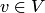 , при чем каждый элемент
, при чем каждый элемент 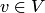 оказывается сопоставленным одному и только одному элементу
оказывается сопоставленным одному и только одному элементу 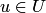 . Взаимно однозначное соответствие будем обозначать
. Взаимно однозначное соответствие будем обозначать 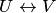 , а соответствующие элементы:
, а соответствующие элементы:  .Два линейных пространства
.Два линейных пространства 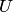 и
и 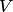 называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что выполняются условия:
называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что выполняются условия:
1) сумме векторов пространства 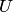 соответствует сумма соответствующих векторов пространства
соответствует сумма соответствующих векторов пространства 
2) произведению числа на вектор пространства 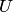 соответствует про изведение того же числа на соответствующий вектор пространства
соответствует про изведение того же числа на соответствующий вектор пространства 
Другими словами, изоморфизм — это взаимно однозначное соответствие, сохраняющее линейные операции.Два объекта, между которыми существует изоморфизм, называются изоморфными. В частности, тождественный морфизм является изоморфизмом, поэтому любой объект изоморфен сам себе.
ГОМОМОРФИЗМ ( (от греч. ὁμός – равный и μορφή – образ) (в математике и л о г и к е). Г. называют такое соответствие между двумя системами объектов с определенными для этих объектов отношениями, при к-ром: 1) каждому объекту первой системы поставлен в соответствие ровно один объект второй еистемы и каждому отношению первой системы поставлено в соответствие ровно одно отношение второй системы; 2) если для нек-рых объектов а, b, с,... первой системы выполняется нек-рое отношение S первой системы, то для объектов а', b', с',... второй системы, соответствующих объектам а, b, с,..., выполняется отношение S' второй системы, соответствующее отношению S. Вторая система объектов и отношений называется при этом гомоморфным образом первой.
О гомоморфном образе какой-либо системы можно в определенном смысле говорить как о модели этой системы. В том частном случае, когда, во-первых, установленное между рассматриваемыми системами соответствие взаимнооднозначно и, во-вторых, отношение S' выполняется во второй системе между объектами а', b', с',... только тогда, когда соответствующее отношение S выполняется между соответствующими объектами а, b, с,... первой системы, Г. называют изоморфизмом.
Два объекта, между которыми существует изоморфизм, называются изоморфными
Эндоморфизм - отображение множества в себя, сохраняющее алгебраические операции и отношения, которые определены на этом множестве. Морфизма, в которых начало и конец совпадают, называют эндоморфизмами
Эндоморфизмы, которые одновременно являются изоморфизм, называются автоморфизмов.
АВТОМОРФИЗМ графа - изоморфное отображение графа на себя (см. Графов изоморфизм). Множество всех автоморфизмов данного графа образует группу относительно операции композиции автоморфизмов. Автоморфизмы графа Gпорождают группу подстановок вершин Г(G), наз. группой (или иногда вершинной группой) графа G, и группу подстановок ребер Г 1(G), наз. реберной группой графа G. Реберная п вершинная группы графа G без петель и кратных ребер изоморфны тогда и только тогда, когда граф G имеет не более одной изолированной вершины и никакая его компонента связности не является изолированным ребром.
Для каждой конечной группы Fсуществует граф, группа автоморфизмов к-рого изоморфна F. В то же время существуют группы подстановок на множестве из пэлементов, не являющиеся вершинной группой никакого графа с пвершинами. С Г. а. можно связать различные типы и меры симметрии графа. Асимметричным называется граф, не имеющий автоморфизмов, отличных от тождественного. При n Ю 4 почти все графы с пвершинами являются асимметричными.