Для экспоненциального сглаживания ряда используется рекуррентная формула:
 (1.8.43)
(1.8.43)
где St —значение экспоненциальной средней в момент t;  -параметр сглаживания,
-параметр сглаживания,  -const, 0<
-const, 0<  <1.
<1.
Величина St оказывается взвешенной суммой всех членов ряда. Причем веса отдельных уровней ряда убывают по мере их удаления в прошлое соответственно экспоненциальной функции (в зависимости о «возраста» наблюдений). Именно поэтому величина St названа экспоненциальной средней.
При высоком значении  дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда. С уменьшением
дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда. С уменьшением  дисперсия экспоненциальной средней сокращается, возрастает ее отличие от дисперсии ряда. Тем самым экспоненциальная средняя начинает играть роль «фильтра», поглощающего колебания временного рада.
дисперсия экспоненциальной средней сокращается, возрастает ее отличие от дисперсии ряда. Тем самым экспоненциальная средняя начинает играть роль «фильтра», поглощающего колебания временного рада.
Таким образом, с одной стороны, следует увеличивать вес более свежих наблюдений, что может быть достигнуто повышением  , а с другой стороны, для сглаживания случайных отклонений значений
, а с другой стороны, для сглаживания случайных отклонений значений  нужно уменьшить. Эти два требования находятся в противоречии. Поиск компромиссного значения параметра сглаживания
нужно уменьшить. Эти два требования находятся в противоречии. Поиск компромиссного значения параметра сглаживания  составляет задачу оптимизации.
составляет задачу оптимизации.
При расчете экспоненциальной средней в момент времени t всегда требуется значение экспоненциальной средней в предыдущий момент времени, поэтому на первом шаге должно быть определено некоторое значение S0, предшествующее St. Часто на практике в качестве начального значения S0 используется среднее арифметическое значение из всех имеющихся уровней временного рада или какой-то их части. Для длинных временных рядов влияние неудачного выбора S0 погашается. Однако, при малых выборках это может привести к существенным ошибкам, так как, например, при а=0,1, даже после 20 итераций вес начального значения S0 превышает веса других уровней ряда. Для элиминирования избыточного веса может быть использована модифицированная процедура:
 (1.8.44)
(1.8.44)
Тогда на первой интеграции при  =0,1 вес текущего уровня
=0,1 вес текущего уровня 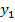 определяется выражением
определяется выражением
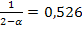 , а вес
, а вес  уже равен меньшему значению
уже равен меньшему значению 
Экспоненциальное сглаживание — это пример самообучающейся модели. К ее безусловным достоинствам относится чрезвычайная простота вычислений, выполняемых итеративно, причем массив прошлой информации уменьшен до единственного значения  .
.
Метод гармонических весов
Данный метод близок к методу экспоненциального сглаживания, поскольку использует примерно тот же принцип. В его основе лежит взвешивание скользящего показателя, но вместо скользящей средней используется идея скользящего тренда.
Экстраполяция проводится по скользящему тренду отдельные точки ломаной линии взвешиваются с помощью гармонических весов, что позволяет более поздним наблюдениям придать больший вес. При использовании данного метода период времени, за который изучается экономический процесс (ретроспективный период), должен быть достаточно длительным, чтобы можно было определить его закономерность. Для осуществления прогноза данным методом исходный ряд динамики разбивается на фазы к. Число фаз должно быть меньше числа уровней ряда n, то есть к<n. Для каждой фазы рассчитывается линейный тренд:
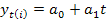 (1.8.45)
(1.8.45)
i=1,2,…n-k+1
При этом для:
i=1 t=1,2,..k
i=2 t=2,3,..k+1
i=3 t=3,4,..k+2
i=n-k+1 t=n-k+1,n-k+2,...n.
С помощью n-k+I уравнений определяются значения скользящего тренда. С этой целью выделяются те значения 
для которых t=1, их обозначают  . Пусть их будет т. Затем находится среднее значение
. Пусть их будет т. Затем находится среднее значение  по формуле средней арифметической.
по формуле средней арифметической.
Далее рассчитываются приросты по формуле:
 (1.8.46)
(1.8.46)
Средняя приростов вычисляется по формуле:
 (1.8.47)
(1.8.47)
Где 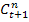 —гармонические коэффициенты, удовлетворяющие следующим условиям:
—гармонические коэффициенты, удовлетворяющие следующим условиям:
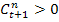 и
и  (1.8.48)
(1.8.48)
Данное выражение позволяет более поздней информации придать большие веса, так как приросты обратно пропорциональны времени, которое отделяет раннюю информацию от поздней для момента t+n.
Если самая ранняя информация имеет вес
 то вес информации, относящейся к следующему моменту времени, равен:
то вес информации, относящейся к следующему моменту времени, равен:
 (1.8.49)
(1.8.49)
В общем виде рад гармонических весов определяется по формуле:
 t=1,2,3,…n-1 (1.8.50)
t=1,2,3,…n-1 (1.8.50)
Чтобы получить гармонические коэффициенты, удовлетворяющие условиям (7.29), нужно гармонические веса  разделить на (n-1), то есть
разделить на (n-1), то есть
 (1.8.51)
(1.8.51)
Далее прогнозирование производится: так же, как и при простых методах, то есть прибавляя к последнему значению рада динамики значение среднего прироста:
 (1.8.52)
(1.8.52)