Задание
Задание 1. Путем опроса получены следующие данные (
):
8 4 4 7 5 5 5 3 10 2 3 6 7 6 10 6 7 7 6 10 7 6 8 10 7 7 9 1 3 4
7 4 4 5 4 9 6 5 9 5 6 5 6 4 7 2 5 7 6 7 3 8 8 7 4 7 5 7 6 6
5 6 6 6 12 5 11 8 1 10 10 9 1 4 5 6 8 4 10 8
а) Составить статистическое распределение выборки, предварительно записав дискретный вариационный ряд.
б) Построить полигон частот.
в) Составить ряд распределения относительных частот.
г) Составить эмпирическую функцию распределения.
д) Построить график эмпирической функции распределения.
е) Найти основные числовые характеристики вариационного ряда (по возможности использовать упрощающие формулы для их нахождения): 1) выборочное среднее 
, 2) выборочную дисперсию D(X), 3) выборочное среднее квадратическое отклонение 
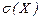, 4) коэффициент вариации V. 5) Пояснить смысл полученных результатов.
Задание 3. Дана выборка
| -2 | -1 | ||||||||||||||||||
1. Провести группировку данных. число интервалов k вычислить по формуле 
, где n – объем выборки. Записать группирированный статистический ряд распределения выборки.
2. Построить гистограмму относительных частот и выдвинуть гипотезу о законе распределения изучаемого признака Х.
3. Провести проверку нулевой гипотезы, используя χ2 - критерий Пирсона при уровне значимости 
. После принятия гипотезы построить график плотности распределения.
Задание 4. Зависимость между показателями X и Y приведена в таблице:
| Х | ||||||||||
| Y |
Построить поле корреляции.
2. Полагая, что между X и Y имеет место линейная корреляционная связь, найти выборочное уравнение прямой линии регрессии
и выборочный коэффициент корреляции 
.
Построить линию регрессии.
4. Сделать вывод о направлении и тесноте связи между показателями X и Y.
Задание 1.
Путем опроса получены следующие данные ():
8 4 4 7 5 5 5 3 10 2 3 6 7 6 10 6 7 7 6 10 7 6 8 10 7 7 9 1 3 4
7 4 4 5 4 9 6 5 9 5 6 5 6 4 7 2 5 7 6 7 3 8 8 7 4 7 5 7 6 6
5 6 6 6 12 5 11 8 1 10 10 9 1 4 5 6 8 4 10 8
а) Составить статистическое распределение выборки, предварительно записав дискретный вариационный ряд.
б) Построить полигон частот.
в) Составить ряд распределения относительных частот.
г) Составить эмпирическую функцию распределения.
д) Построить график эмпирической функции распределения.
е) Найти основные числовые характеристики вариационного ряда (по возможности использовать упрощающие формулы для их нахождения): 1) выборочное среднее , 2) выборочную дисперсию D(X), 3) выборочное среднее квадратическое отклонение 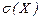, 4) коэффициент вариации V. 5) Пояснить смысл полученных результатов.
РЕШЕНИЕ:
а) Составить статистическое распределение выборки, предварительно записав дискретный вариационный ряд.
Для составления дискретного вариационного ряда отсортируем данные опроса по величине и расположим их в порядке возрастания
111 22 3333 4444444444 555555555555 666666666666666
77777777777777 8888888 9999 10101010101010 11 12
Более компактно эти данные можно представить в виде статистического распределения выборки (в виде табл. 1, в которой первая строка – варианты (наблюдаемые значение), вторая строка – частоты появления этих вариант).
| xi | ||||||||||||
| ni |
б) Для построения полигона частот найдем относительные частоты (
, где 
, где m – число различных значений признака X (
) и в данном примере 
), которые будем вычислять с одинаковой точностью. Полигон частот – ломаная линия, соединяющая точки с координатами 
. Расчеты запишем в табл. 2.
Таблица 2
| xi | ni | Относительная
частоты ( )
| Накопленные Частоты |
| 0,0375 | 0,0375 | ||
| 0,025 | 0,0625 | ||
| 0,05 | 0,1125 | ||
| 0,125 | 0,2375 | ||
| 0,15 | 0,3875 | ||
| 0,1875 | 0,575 | ||
| 0,175 | 0,75 | ||
| 0,0875 | 0,8375 | ||
| 0,05 | 0,8875 | ||
| 0,0875 | 0,975 | ||
| 0,0125 | 0,9875 | ||
| 0,0125 | |||
| сумма | 1,000 |
Изобразим полигон частот вариационного ряда
в) Запишем ряд распределения относительных частот в виде таблицы 3, в которой первая строка – варианты (изучаемый признак), вторая строка – относительные частоты (частости) .
| xi | ||||||||||||
| wi | 0,0375 | 0,025 | 0,05 | 0,125 | 0,15 | 0,1875 | 0,175 | 0,0875 | 0,05 | 0,0875 | 0,0125 | 0,0125 |
г) Эмпирическую функцию распределения найдем, используя накопленные частоты (табл. 2, столбик 4) и следующую формулу:
Таким образом, эмпирическая функция распределения примет вид
д) Построим график эмпирической функции распределения (рис. 2), используя значения полученные в пункте г.
е) Найдем основные числовые характеристики вариационного ряда:
1) Выборочное среднее найдем как среднее арифметическое взвешенное
,
которое характеризует среднее значение признака X в пределах рассматриваемой выборки.
2) Выборочную дисперсию
,
которая является мерой рассеяния возможных значений показателя X вокруг своего среднего значения. Его размерность совпадает с квадратом размерности варианты.
3) Выборочное среднее квадратическое отклонение
,
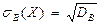которое описывает абсолютный разброс значений показателя X. Его размерность совпадает с размерностью варианты.
Примечание. При малых n 
вычисляют «исправленную» дисперсию:
,
и исправленное стандартное отклонение 
.
4) Коэффициент вариации
,
который характеризует относительную изменчивость показателя X, то есть относительный разброс вокруг его среднего значения 
. Коэффициент вариации является безмерной величиной, поэтому он пригоден для сравнения рассеяния вариационных рядов, варианты которых имеют различную размерность.
Используя приведенные выше формулы, вычислим выборочное среднее и выборочную дисперсию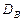 
. Для этого составим расчетную табл. 4.
Таблица 4.
| n i | 
| 
| 
| |
| 26,5225 | 79,5675 | |||
| 17,2225 | 34,445 | |||
| 9,9225 | 39,69 | |||
| 4,6225 | 46,225 | |||
| 1,3225 | 15,87 | |||
| 0,0225 | 0,3375 | |||
| 0,7225 | 10,115 | |||
| 3,4225 | 23,9575 | |||
| 8,1225 | 32,49 | |||
| 14,8225 | 103,758 | |||
| 23,5225 | 23,5225 | |||
| 34,2225 | 34,2225 | |||
| Сумма | 444,2 |
Используя суммы, полученные в табл. 4, найдем:
1) Выборочную среднюю
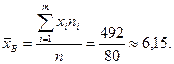
2) Выборочную дисперсию
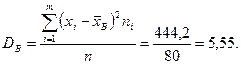
Замечание. Если первоначальные варианты – большие числа или, наоборот, слишком малы и к тому же являются равноотстоящими, то удобно перейти к условным вариантам
,
где с и k – произвольные числа.
В качестве с целесообразно выбирать одно из средних значений признака X, а в качестве k – разность между двумя соседними вариантами. В этом случае формулы для упрощенного вычисления принимают следующий вид:
– выборочная средняя
;
– и выборочная дисперсия
.
Для вычисления основных числовых характеристик воспользуемся упрощающими формулами, для чего составим расчетную табл. 5. Выберем 
и 
| xi | n i |
| 
| 
|
| -2 | -6 | |||
| -1 | -2 | |||
| Сумма |
Используя суммы, полученные в таблице, найдем:
1) Выборочную среднюю
.
2) Выборочную дисперсию
.
3) Выборочное среднее квадратическое отклонение
.
4) Коэффициент вариации
.
5) Смысл полученных результатов заключается в том, что величина 
характеризует среднее значение признака X, то есть среднее значение составило 6,15. Среднее квадратическое отклонение 
описывает абсолютный разброс значений показателя X и в данном случае составляет 
. Коэффициент вариации V характеризует относительную изменчивость показателя X, то есть относительный разброс вокруг его среднего значения , и в данном случае составляет 
.
Задание 2.
Дана выборка
| -2 | -1 | ||||||||||||||||||
1. Провести группировку данных. число интервалов k вычислить по формуле , где n – объем выборки. Записать группирированный статистический ряд распределения выборки.
2. Построить гистограмму относительных частот и выдвинуть гипотезу о законе распределения изучаемого признака Х.
3. Провести проверку нулевой гипотезы, используя χ2 - критерий Пирсона при уровне значимости . После принятия гипотезы построить график плотности распределения.
Найдем к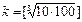 
=10.
| xi | -2 | -1 | ||||||||||||||
| ni |
| xi | -2 -0,4 | -0,4 1,2 | 1,2 2,8 | 2,8 4,4 | 4,4 | 7,6 | 7,6 9,2 | 9,2 10,8 | 10,8 12,4 | 12,4 | итого |
| ni |
выборочную дисперсию 
найдем по упрощенной формуле
,
где выборочную среднюю 
найдем также по упрощенной формуле
.
Составим расчетную таблицу для нахождения необходимых сумм при 
и 
Таблица 9.
| Стаж работы по специальности | Середина интервала xi | Количество студентов n i |
| 
| 
|
| (-2-0,4) | -1,2 | -3,2 | -6,4 | 20,48 | |
| (-0,4 1,2) | 0,4 | -2,4 | -9,6 | 23,04 | |
| 1,2 2,8 | -1,6 | -11,2 | 17,92 | ||
| 2,8 4,4 | 3,6 | -0,8 | -16,8 | 13,44 | |
| 4,4 6 | 5,2 | ||||
| 6 7,6 | 6,8 | 0,8 | 10,4 | 8,32 | |
| 7,6 9,2 | 8,4 | 1,6 | 25,6 | 40,96 | |
| 9,2 10,8 | 2,4 | 9,6 | 23,04 | ||
| 10,8 12,4 | 11,6 | 3,2 | 6,4 | 20,48 | |
| 12,4 14 | 13, | ||||
| СУММА | 199,68 |
Тогда выборочная средняя
Выборочная дисперсия
.
Параметры теоретического нормального закона распределения 
и 
, являющиеся соответственно математическим ожиданием и дисперсией случайной величины X, неизвестны, поэтому заменяем их «наилучшими» оценками по выборке – несмещенными и состоятельными оценками соответственно выборочной средней и «исправленной» выборочной дисперсией 
. Так как число наблюдений 
достаточно велико, то вместо исправленной 
можно взять «обычную» выборочную дисперсию 
. было найдено 
; 
. Тогда 
.
Так как случайная величина имеет нормальное распределение, то для расчета вероятностей попадания случайной величины X в интервал 
, где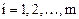 
, используем функцию Лапласа в соответствии со свойствами нормального распределения:
Так как нормальное распределение определено на всей числовой оси, то есть 
, то указанная выше формула применяется при нахождении вероятностей попадания случайной величины X в интервал для всех значений случайной величины X, за исключением крайних значений, то есть 
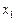и 
.
При нахождении вероятности попадания случайной величины X в интервал 
полагаем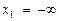 
, то есть искомая вероятность будет определяться следующей формулой:
В силу нечетности функции Лапласа 
, то есть 
, находим значения функции Лапласа для отрицательных аргументов,
При нахождении вероятности попадания случайной величины X в интервал 
, полагаем 
, то есть искомая вероятность будет определяться следующей формулой
Таким образом, в нашем примере получим:
| xi | -2 -0,4 | -0,4 1,2 | 1,2 2,8 | 2,8 4,4 | 4,4 | 7,6 | 7,6 9,2 | 9,2 10,8 | 10,8 12,4 | 12,4 | итого |
1) 
2) 
3) 
4) 
5) 
6) 
7) 
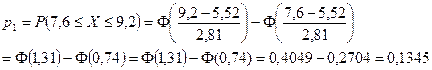
8) 
9) 
10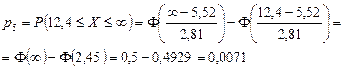 
Для определения выборочной статистики (2)
,
где 
– теоретические частоты, составим расчетную табл.10.
Таблица 10.
| i |
Интервал
|
Эмпирические частоты
|
Вероятности
|
Теоретические частоты
|
|
|
| |
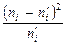
| (-2-0,4) | 0,0174 | 1,74 | 0,0676 | 0,0389 | 0,02 | |||
| (-0,4 1,2) | 0,0444 | 4,44 | 0,1936 | 0,0436 | 0,04 | |||
| 1,2 2,8 | 0,1042 | 10,42 | 11,6964 | 1,1225 | 0,07 | |||
| 2,8 4,4 | 0,1786 | 17,86 | 9,8596 | 0,5520 | 0,21 | |||
| 4,4 6 | 0,2229 | 22,29 | 45,0241 | 2,0199 | 0,29 | |||
| 6 7,6 | 0,2029 | 20,29 | 53,1441 | 2,6192 | 0,13 | |||
| 7,6 9,2 | 0,1345 | 13,45 | 6,5025 | 0,4835 | 0,16 | |||
| 9,2 10,8 | 0,065 | 6,5 | 6,25 | 0,9615 | 0,04 | |||
| 10,8 12,4 | 0,023 | 2,3 | 0,09 | 0,0391 | 0,02 | |||
| 12,4 14 | 0,0071 | 0,71 | 1,6641 | 2,3438 | 0,02 | |||
| 10,2241 |
Из табл. 10 находим фактически наблюдаемое значение статистики (выборочная статистика) 
Так как число интервалов 
, а нормальный закон распределения определяется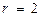 
параметрами, точечные оценки которых были получены по выборочным данным, то число степеней свободы 
. Соответствующее критическое значение статистики 
можно найти по таблице «Критические точки распределения 
» в приложении 3 настоящих методических указаний или в приложении 5 в книгах [1] или [5]. Имеем 
.
Так как 
, то гипотеза о выбранном теоретическом нормальном законе распределения с параметрами 
и 
не согласуется с опытными данными (в данном примере), то есть гипотеза отвергается на заданном уровне значимости 
.
Изобразить эмпирические распределения можно, например, ступенчатой фигурой, состоящей из прямоугольников с основаниями, равными величинам интервалов 
, и высотами, равными частностям 
(или частотам ) этих интервалов, называемой гистограммой. При построении нормальной кривой для каждого интервала по оси ординат откладываем соответствующие вероятности (теоретические частоты ). Вершина нормальной кривой имеет координаты 
; 
(где 
– малая функция Лапласа, значения которой приведены в приложении 1 настоящих методических указаний или в приложении 1 в книгах [1] или [5]).
Выполнив чертеж можно увидеть, что нормальная кривая теоретического распределения практически не «выравнивает» гистограмму эмпирического распределения.
Задание 3.
Зависимость между показателями X и Y приведена в таблице:
| Х | ||||||||||
| Y |
1. Построить поле корреляции.
2. Полагая, что между X и Y имеет место линейная корреляционная связь, найти выборочное уравнение прямой линии регрессии
и выборочный коэффициент корреляции .
Решение. Построим диаграмму рассеяния отметив в прямоугольной декартовой системе координат точки с координатами 
– эмпирические данные. Из диаграммы рассеяния видно, что между показателями X и Y действительно наблюдается линейная связь.
Для определения коэффициентов выборочного уравнения регрессии 
можно воспользоваться, например, следующими формулами
,
,
,
,
.
Тогда параметры 
и 
уравнения линейной регрессии и выборочный коэффициент линейной корреляции 
определим по формулам
,
,
.
| x | y | x 2 | y 2 | xy | |
| сумма |
Используя суммы, найдем:
,
,
,
,
,
.
Тогда выборочное уравнение линейной регрессии примет вид
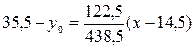
или
- 
.
Выборочный коэффициент линейной корреляции
3. Построить линию регрессии.
Для построения линии регрессии (прямой) найдем две точки. В качестве одной из них можно выбрать 
, то есть точку 
. Вторую точку найдем из уравнения регрессии . При 
: 
, то есть точка 
.
4. Сделать вывод о направлении и тесноте связи между показателями X и Y.
Таким образом, расчеты подтвердили, что между показателями X и Y наблюдается положительная линейная корреляционная связь (связь прямая, так как 
), которую согласно таблице Чеддока можно считать весьма высокой (
).
Библиографический список
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд 4-е, стер. – М.: Высш. шк., 1998. – 400 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. II: Учеб. пособие для втузов. – 5-е изд., испр. – М.: Высш. шк., 1997. – 416 с.
3. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. В 2-х частях. Ч. II. Теория вероятностей и математическая статистика. Линейное программирование. – М.: Высшая школа, 1982.
4. Бронштейн И.Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука, 1986.
5. Гмурман В.Е. Теории вероятностей и математическая статистика: Учеб. пособие для вузов. Изд 6-е, стер. –М.: Высш. шк.,1998. – 479 с.
6. Кремер Н.Ш. Математическая статистика. Учебное пособие/ ВЗФЭИ. – М.: Экономическое образование, 1992. – 112 с.
7. Вентцель Е.С. Теория вероятностей: Учеб. для вузов. – 5-е изд. стер. – М.: Высш. шк., 1998. – 576 с.