Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технологический университет»
МГУПИ
Кафедра КБ-3 «Управление и моделирование систем»
Отчет №3 о выполнении
Лабораторной работы по предмету
«Численные методы»
Тема: «Методы интерполяции: полином Лагранжа, кусочно-полиномиальная интерполяция, интерполяция сплайнами»
Выполнил:
Студент 2 курса,
Группы БИСО-01-15
№ студ. Билета 15Б0069
Азерский Владислав Дмитриевич
Проверил: Серов В.А.
Москва 2017
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Интерполяция – это задача нахождения промежуточных значений величины по имеющемуся дискретному набору значений.
Пусть функция 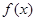 задана таблицей n значений:
задана таблицей n значений:

| 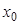
| 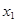
| 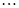
| 
|
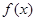
| 
| 
| 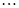
| 
|
То есть 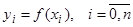 .
.
Точки 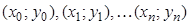 называются интерполяционными узлами.
называются интерполяционными узлами.
Задача интерполяции состоит в том, чтобы вычислить значение 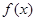 в точке
в точке  .
.
Решается эта задача построением по исходной информации из таблицы функции  , которая близка к
, которая близка к 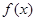 и имеет аналитическое представление. После этого предполагается, что
и имеет аналитическое представление. После этого предполагается, что 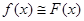 , и
, и  используется для получения неизвестного значения
используется для получения неизвестного значения 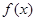 .
.
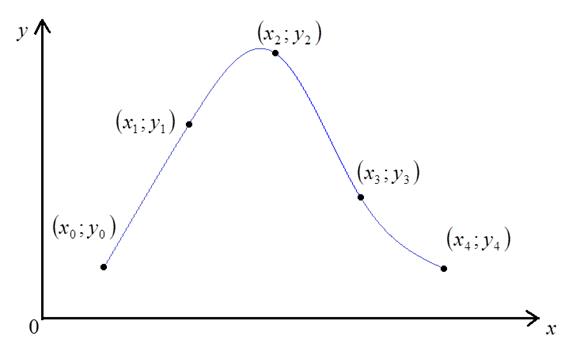
Классическая постановка задачи интерполяции состоит в построении такой функции  , что
, что  .
.
Кусочно-полиномиальная интерполяция
Кусочно-полиномиальная интерполяция используется для большого числа интерполяционных узлов, когда от одного полинома проку мало. Суть данного метода в том, что отрезок разбивается на подотрезки, на каждом из которых строится свой полином. Важное условие – на концах этих отрезков линия не должна прерываться.
Рассмотрим кусочно-полиномиальную интерполяцию на следующей задаче.

| |||||
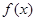
| 1.0 | 1.8 | 2.2 | 1.4 | 1.0 |
Разобьём отрезок 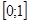 на части
на части 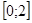 и
и 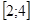 , и построим многочлены Лагранжа соответственно
, и построим многочлены Лагранжа соответственно 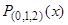 и
и  .
.
В результате вычислений получается:


Главное условие кусочно-полиномиальной интерполяции 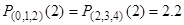 выполняется.
выполняется.
Но, с другой стороны, если посчитать производные, то мы увидим основной недостаток данного метода:
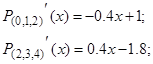
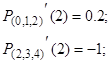
В точке соединения двух полиномов 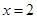 первая производная имеет разрыв, то есть функция
первая производная имеет разрыв, то есть функция 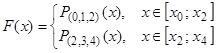 не обладает свойством гладкости.
не обладает свойством гладкости.
На практике часто требуется, чтобы аппроксимирующая функция была гладкой (чтобы производная была непрерывна). Тогда метод кусочно-полиномиальной интерполяции неприменим.
Интерполяция сплайнами
Интерполяция сплайнами придумана для того, чтобы избежать главный недостаток кусочно-полиномиальной интерполяции и построить гладкую функцию. Такая интерполяция сочетает в себе глобальную гладкость и локальную простоту функции по сравнению с другими интерполяциями.
Пусть 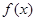 задана таблицей:
задана таблицей:

| 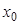
| 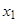
| 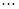
| 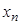
|
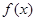
| 
| 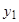
| 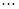
| 
|
Назовём функцию 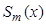 интерполяционным сплайном порядка n для функции
интерполяционным сплайном порядка n для функции 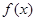 на отрезке
на отрезке 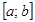 , если выполнены следующие условия:
, если выполнены следующие условия:
1. На всём отрезке 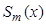 имеет непрерывные производные до порядка
имеет непрерывные производные до порядка  включительно.
включительно.
2. На каждом из частичных отрезков 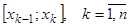
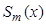 является многочленом степени
является многочленом степени  .
.
3.  для
для 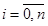 .
.
Дефект сплайна – это разность 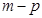 .
.
Самый распространённый вид сплайна – это кубический сплайн с дефектом 1. Рассмотрим его.
По определению сплайн 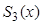 на любом
на любом  отрезке
отрезке  является многочленом
является многочленом  порядка -
порядка - 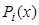 :
:
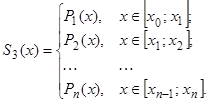
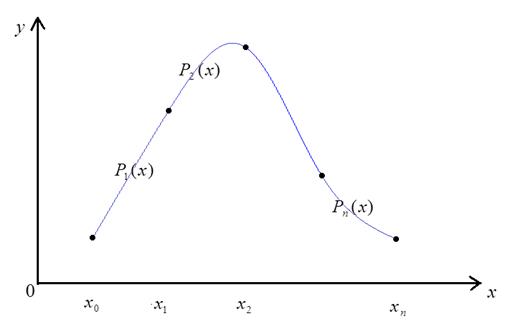
Раз это – кубический многочлен, то мы будем искать 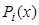 по следующей формуле:
по следующей формуле:
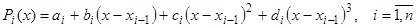 ,
,
где коэффициенты неизвестны и именно их и надо найти – всего  неизвестных.
неизвестных.
По определению сплайна должны выполняться условия совпадения 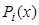 в узлах интерполяции:
в узлах интерполяции:

Через 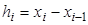 мы обозначили шаг между текущим и предыдущим узлами интерполяции.
мы обозначили шаг между текущим и предыдущим узлами интерполяции.
Итак, мы получили  линейных алгебраических уравнений. Чтобы получить оставшиеся
линейных алгебраических уравнений. Чтобы получить оставшиеся  , потребуем непрерывности производных на отрезке
, потребуем непрерывности производных на отрезке 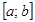 . Так как мы составляем сплайн 3 порядка с дефектом 1, то необходимо выполнить непрерывность
. Так как мы составляем сплайн 3 порядка с дефектом 1, то необходимо выполнить непрерывность  производных – первой
производных – первой 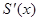 и второй
и второй 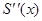 :
:

Обратите внимание, что эти условия должны выполняться только на внутренних точках, а не на крайних, поэтому внешние точки исключаем из рассмотрения:

Считаем производные:
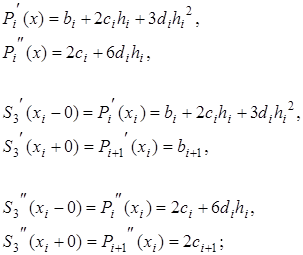
Приравнивая левые и правые соответствующие производные, получаем ещё 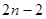 линейных алгебраических уравнений:
линейных алгебраических уравнений:

Недостаёт ещё двух уравнений, которыми мы должны описать поведение производных на крайних точках. Для их получения используют какие-либо требования к поведению сплайна в граничных точках интервала 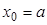 и
и 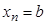 .
.
Выдвигаемые требования могут быть разные. Достаточно вторую производную в этих точках приравнять к каким-либо числам 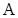 и
и  . Самое простое требование – это требование нулевой кривизны – положить эти числа равными нулю.
. Самое простое требование – это требование нулевой кривизны – положить эти числа равными нулю.
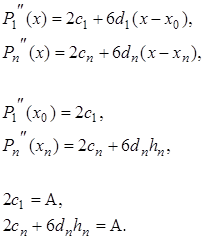
Теперь все  уравнений выведены и давайте соберём их в одну СЛАУ:
уравнений выведены и давайте соберём их в одну СЛАУ:
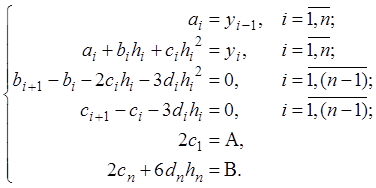
Исключим из этой системы  , так как они уже известны, и получим:
, так как они уже известны, и получим:
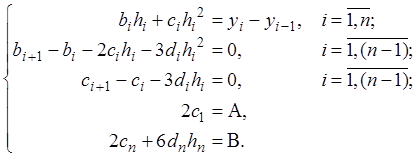
Эта система содержит все необходимые уравнения для получения  . Можно доказать, что решение этой СЛАУ существует.
. Можно доказать, что решение этой СЛАУ существует.
ЛИСТИНГ ПРОГРАММЫ
1. Основной код:
clear, clc
def={''};
optn=struct('Resize','on','WindowStyle','normal','Interpreter','none');
% Диалоговое окно для ввода таблицы (xi, yi):
text_1='Введите значения xi через пробел:';
text_2='Введите значения yi=y(xi) через пробел:';
p_int=inputdlg({text_1, text_2},'Окно ввода',1,[def, def], optn);
a=str2num(p_int{1});
b=str2num(p_int{2});
if ((isempty(a)==1) || (isempty(b)==1))
error('Неправильные входные данные!');
end
interpol(a, b, 0.5, 0.5);
2. Реализация полинома Лагранжа:
function Polynom=lagranj(X, Y)
w = length(X);
n = w - 1;
L = zeros(w, w);
for k = 1:n+1
V = 1;
for j = 1:n+1
if (k ~= j)
V=conv(V, poly(X(j)))/(X(k)-X(j));
end
end
L(k,:) = V;
end
Polynom = Y * L;
end
function y = lagranj_f_x(P,value)
xx = value;
y = 0;
w = length(P);
for i = 1:w
y = y + xx^(w - i) * P(i);
end
end
3. Реализация кусочно-полиномиальной интерполяции:
function [pl_y] = piece_poli(x, f_x)
P = lagranj(x, f_x);
a = x(1);
b = x(length(x));
pl = a:(b-a) / 60:b;
pl_y = [];
k = 1;
for i = a:(b-a) / 60:b
pl_y(k) = lagranj_f_x(P, i);
k = k + 1;
end
end
è смотри функцию interpol.
4. Реализация интерполяции кубическими сплайнами:
function s = spline_poli(x, f_x, dx0, dxn)
%dx0 = s'(x0); - граничное условие на первую производную
%dxn = s'(xn); - граничное условие на первую производную
n = length(x) - 1;
h = diff(x);
d = diff(f_x)./h;
a1 = h(2:n - 1);
b1 = 2 * (h(1:n-1) + h(2:n));
c = h(2:n);
u= 6 * diff(d);
b1(1) = b1(1) - h(1) / 2;
u(1) = u(1) - 3 * (d(1) - dx0);
b1(n - 1) = b1(n - 1) - h(n) / 2;
u(n - 1) = u(n - 1) - 3 * (dxn - d(n));
for k = 2:n-1
temp = a1(k - 1) / b1(k - 1);
b1(k) = b1(k) - temp * c(k - 1);
u(k) = u(k) - temp * u(k - 1);
end
m(n) = u(n - 1) / b1(n - 1);
for k = n - 2:-1:1
m(k + 1) = (u(k) - c(k) * m(k + 2)) / b1(k);
end
m(1) = 3 * (d(1) - dx0) / h(1) - m(2)/2;
m(n + 1)=3 * (dxn-d(n)) / h(n) - m(n) / 2;
for k = 0:n-1
s(k + 1, 1) = (m(k + 2) - m(k + 1)) / (6 * h(k + 1));
s(k + 1, 2) = m(k + 1) / 2;
s(k + 1, 3) = d(k + 1) - h(k + 1) * (2 * m(k + 1) + m(k + 2)) / 6;
s(k + 1, 4) = f_x(k + 1);
end
end
function y=spline_f_x(ar,value)
xx=value;
y=0;
w=length(ar)-1;
for i=0:w
y=y+ xx^(w-i) * ar(i+1);
end
end
5. Функция, в которой осуществляется вызов предыдущих функций:
function interpol(x, f_x, dx0, dxn)
points = 0;
a = x(1);
b = x(length(x));
z = 1;
distant = [];
distant_y = [];
m = 1;
pl = [];
pl_y = [];
f = false;
% Кусочно-полиномиальная интерполяция:
for i = 1:length(x)
distant(z)=x(i);
distant_y(z)=f_x(i);
if (z == 3)
pl_y(((m - 1) * 61 + 1):(m * 61)) = piece_poli(distant, distant_y);
points = points + 60;
if(f)
points = points + 1;
end
f = true;
distant = [];
distant_y = [];
z = 1;
m = m + 1;
distant(z) = x(i);
distant_y(z) = f_x(i);
end
z = z + 1;
end
% График (кусочно-полиномиальная):
hold on;
pl = a:(b - a) / points:b;
plot(pl, pl_y, 'b');
grid on;
xlabel('Координата по Ox');
ylabel('Координата по Oy');
% Интерполяция кубическими сплайнами:
s = spline_poli(x, f_x, dx0, dxn);
pl_kyb = [];
pl_kyp_y = [];
points = 0;
a = x(1);
b = x(length(x));
m = 1;
y = [];
for i = 1:1:length(x) - 1
for j = x(i):0.1:x(i + 1)
y(m) = spline_f_x(s(i,:),j - x(i));
xx(m) = j;
m = m + 1;
end
end
% График (полином Лангранжа):
zz(1:61) = piece_poli(x,f_x);
z = a:(b - a)/60:b;
plot(z,zz,'m');
%xx_ = 0:(b-a)/60:4;
%yy = spline(x,f_x,xx_);
%plot(x,f_x,'y',xx_,yy)
% График (куб. сплайны):
plot(xx, y, 'g');
legend('Кусочно-полиномиальная','Полином Лангранжа','Куб. сплайны',...
'Location','southwest');
x1 = [];
y1 = [];
for i = 1:length(x) - 1
x1(i,:) = i - 1:0.1:i;
y1(i,:) = polyval(s(i,:), x1(1,:));
end
c = a:1:b;
plot(c, f_x, 'ko');
hold off;
end
ДЕМОНСТРАЦИЯ РАБОТЫПРОГРАММЫ
Задача №1:
Функция задана таблицей:
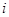
| |||||
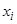
| |||||
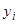
| 1.0 | 1.8 | 2.2 | 1.4 | 1.0 |
Требуется воспользоваться методами интерполяции.
Этапы решения задачи:
1) Вводим значения x и y из таблицы в поля диалогового окна:
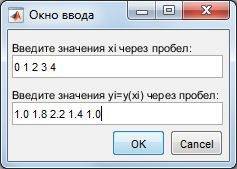
2) Вывод графиков:
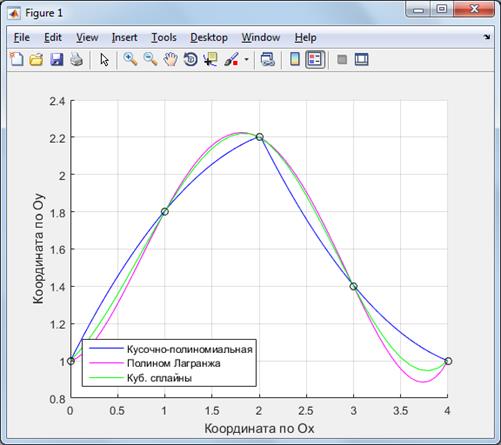
Задача №2:
Функция задана таблицей:
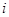
| ||||
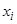
| -1 | |||
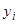
| 0.5 | 1.0 | 2.0 | 4.0 |
Требуется воспользоваться методами интерполяции.
Этапы решения задачи:
1) Вводим значения x и y из таблицы в поля диалогового окна:
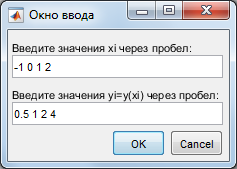
2) Вывод графиков:
