МЕТОД МОНТЕ-КАРЛО
КРАТКАЯ ТЕОРЕТИЧЕСКАЯ СПРАВКА
ОБЩАЯ ХАРАКТЕРИСТИКА МЕТОДА
Во многих задачах исходные данные носят случайный характер. Например, при расчете надежности случайной конструкции, состоящей из многих элементов не известны точно (и даже приближенно) моменты отказа каждого элемента. Каждый элемент обычно испытывают на изготовляющем заводе и снимают так называемую кривую отказов p(t) - вероятность выхода из строя элемента после £t часов работы. Определять экспериментальным путем кривую отказов для всей конструкции слишком дорого. Для решения этой и многих других задач применяют метод статистических испыта ний, называемый также методом Монте-Карло.
Основная мысль метода Монте-Карло состоит в следующем. Предположим, имеется некая величина x, могущая принимать различные значения (например, время работы конструкции до отказа; в теории вероятностей x называется случайной величиной), и нужно найти ее среднее значение (в теории вероятностей erо называют математическим ожиданием и обозначают Мx). Для этого осуществляется серия из N независимых случайных математических измерений (принято говорить: испытаний) значений величины x: x1, x2,… xN.и затем приближенно полагается 
Метод Монте-Карло может быть применен и в тех случаях, когда исходные данные имеют вполне определенное значение. Например, опрос всего населения с целью выяснить общественное мнение по какому-либо вопросу в принципе может быть проведен, но является очень дорогим мероприятием. Для достижений этой цели можно опросить лишь часть населения (например, одного человека из каждой тысячи) и мнение этой части принять приближенно за мнение всего населения. Однако, чтобы получить верный результат, необходимо, чтобы выбор опрашиваемых людей был случайным. (Например, опрос городского населения, проводимый по телефону по случайно выбранным номерам, даст нам "среднее мнение" людей, в целом более обеспеченных.). Простым и очень полезным оказывается применение метода Монте-Карло к вычислению объемов и интегралов по сложным областям в n-мерных пространствах.
ВЫЧИСЛЕНИЕ ОБЪЕМОВ И КРАТНЫХ ИНТЕГРАЛОВ METOДOM МОНТЕ-КАРЛО
Пусть требуется вычислить объем n-мерной области G, лежащей в n-мерном параллелепипеде
(1) Т = [a1,b1] ´ [a2,b2] ´…´[an,bn]
Выберем в Т случайным образом какую-либо точку θ. Эта точка с некоторой вероятностью р окажется в области G. Если точку мы выбрали совершенно случайно, то
р =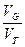 
, где VG и VT - объемы области и параллелепипеда.
Пусть в Т выбрано N точек независимо (то есть так, чтобы выбор одной точки не оказывал никакого влияния на выбор любой другой точки) и пусть из них К точек оказалась в области G. Если N достаточно велико, то, как следует из теории вероятностей, K/N» р. Таким образом, зная объем VT (он легко вычисляется), получаем
(2) 
Приближенное равенство может в принципе оказаться очень неточным, но чем больше N, тем больше вероятность; что равенство (2) окажется более точным.
 |
Примечание. Здесь вкачестве случайной величины x неявно присутствовала следующая функция, зависящая от θ:
Ее среднее значение (равное р) мы находили путем измерения значений x в различных случайно выбранных точках
Пусть теперь требуется вычислить кратный интеграл по области G:
(3) 
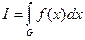
Ясно, что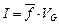 
, 
где 
- среднее значение функции f в области G. Случайный выбор точки θÎG и вычисление значения f(θ) можно рассматривать как однократное испытание случайной величины f(x). Проведем серию из N независимых испытаний, То есть, выберем случайным образом точки θ1, θ2,…, θN Тогда
 |
Если G имеет сложную форму, то интеграл предварительно преобразуют к виду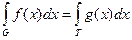 
где T-параллелепипед, содержащий в себе G, а функция
ОЦЕНКА ТОЧНОСТИ ВЫЧИСЛЕНИЯ МЕТОДОМ МОНТЕ - КАРЛО
Для метода Монте-Карло не существует гарантированных оценок точности вычислений. Точность вычисления объема может быть оценена с помощью известного в теории вероятностей правила "трех сигм" следующим неравенством
(4) 
 |
справедливым с вероятностью не менее 99,7%. Здесь сохранены обозначения формулы (2), а величину s характеризующую среднеквадратичный разброс результатов разных испытаний, можно приближенно вычислить (при N > 10) по следующей формуле
(5)
Величина 
называется вероятной.ошибкой. Истинная ошибка D не превосходит R с вероятностью 50%. и обычно удовлетворяет неравенству
0,5R £ D£2R.
Применительно к оценке точности вычисления интегралов правило "трех сигм" дает
следующее неравенство, также верное с вероятность» не менее 99,7%.
 |
(6)
-
где s можно вычислить приближенно (при N > 10) по формуле
(7) 
Замечание 1. Если объем области близок к объему параллелепипеда (»99% от объема Т) или очень мал (»1% от объема Т), то правило «трех сигм» применимо только при очень больших N, иначе оценку точности необходимо проводить по формулам теории вероятностей.
Замечание 2. Метод Монте-Карло обычно дает результат с невысокой относительной точностью (d ³ 0,1%). Зато даваемая им точность не зависит от степени гладкости функций. Поэтому, если функция имеет не более двух непрерывных производных, то вычисление интегралов методом Монте-Карло становится выгодным при пяти измерениях и выше, а если только одну производную, то – уже в трехмерном случае.