Б) Решение вариационных задач методом Ритца.

Прямые методы решения вариационных задач

А) Решение вариационных задач методом конечных разностей

Исследуемая область существования решения разбивается на интервалов, величиной

, (4.43)

где и – границы исследуемой области.

Производные и функции, входящие в выражение функционала, заменяются конечно-разностными выражениями, вследствие чего функционал становится функцией значений в каждой точке этой области. В соответствии с правилами определения экстремума функционала, зависящего от нескольких переменных (Раздел 4.2), полученные выражения функционала дифференцируются по всем переменным . В результате получается система алгебраических уравнений, решение которой позволяет определить значение искомой функции в каждой точке исследуемой области.

Пример: На интервале [0,1] задан функционал . Найти функцию, минимизирующую данный функционал при нулевых краевых условиях.

Решение. 1. Разобьём исследуемую область [0,1] на =5 подынтервалов, величиной .

2. Обозначим значения искомой функции в точках разбиения пространственной координаты следующим образом: ; ; ; ; ; .

3. Заменяем производные функции конечно-разностными выражениями: ; ; ; : .

4. Записываем функционал в виде суммы отдельных составляющих

5. Заменяем производные конечно-разностными выражениями и группируем подобные

6. Дифференцируем полученное выражение по каждой из переменных и приравниваем производные к нулю. В результате получаем алгебраическую систему уравнений, позволяющую определить значения функции , доставляющей функционалу минимум.

; ;

; .

7. Подставляя в полученные уравнения значения координат ; ; ; , значения функций на границах исследуемой области и , выполняя промежуточные преобразования, в окончательном виде получим систему:

; Решая систему традиционными методами, получим: ,

; , ; .

;

.

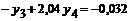Точное решение уравнения Эйлера: ; ; ; .

Сравнение точного решения с приближённым свидетельствует о высокой точности последнего даже при малом числе разбиения пространственной координаты.

Для решения вариационных задач широкое распространение получил метод Ритца.

б) Решение вариационных задач методом Ритца.

Идея метода Ритца заключается в следующем. Для минимизации функционала в качестве искомой задают пробную функцию с неизвестными коэффициентами, удовлетворяющую краевым условиям. Чаще всего в качестве пробной, функции используется алгебраический полином 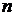-го порядка , (4.44)

где ; ; ; .

Основным условия выбора вида пробной функции является то, чтобы она удовлетворяла краевым условиям. Если, например, краевые условия заданы в виде ; , то пробную функцию рационально представить в виде полинома . с тем чтобы и .

Подставляя пробную функцию в выражение функционала, выполняя промежуточные преобразования и интегрируя полученное подынтегральное выражение в пределах исследуемой области, получают полином, являющийся функцией коэффициентов пробной функции. Руководствуясь правилами отыскания экстремума функции нескольких переменных (Раздел 4.2), полученное выражение дифференцируют по каждому искомому коэффициенту. В результате получают систему уравнений относительно неизвестных коэффициентов пробной функции. Определив значения этих коэффициентов, восстанавливают вид пробной функции, минимизирующей исследуемый функционал.

Для иллюстрации этого метода рассмотрим приведённый выше пример, решив его методом Ритца.

Пример. На интервале [0,1] задан функционал .

Найти функцию, минимизирующую данный функционал, при нулевых краевых условиях первого рода.

Решение. Пробную функцию задаём в виде , удовлетворяющем краевым условиям. Производная пробной функции имеет вид .

Подставляя выражение пробной функции и её производной в функционал

Выполняя преобразования, группируя подобные и выполняя интегрирование в указанных пределах, получим .

Для определения коэффициентов пробной функции воспользуемся условиями минимизации функционала: приравняем к нулю производные функционала по каждому из искомых коэффициентов ; . Решая систему двух уравнений с двумя неизвестными, определим их значения: ; и решение вариационной задачи имеет вид .

Сравним решение вариационной задачи, полученное рассмотренным выше конечно-разностным методом, методом Ритца с точным аналитическим решением, которое записывается следующим образом .

В первой строке таблицы приведены значения минимизирующей функции, полученные конечно-разностным методом, во второй - методом Ритца, в третьей - точное решение.

		0,2	0,4	0,6	0,8	1,0
, мкр
, м.Ритца		- 0,02855	- 0,05064	- 0,05845	-0,04418
Аналитическое		-0,02868	-0,05048	-0,05826	0,04429

Сравнение результатов приближённых значений с точным аналитическим решением показывает высокую точность приближённых методов, несмотря на довольно грубое деление исследуемой области. Точность решения может быть повышена за счёт увеличения числа интервалов разбиения пространственной координаты при использовании метода конечных разностей и увеличения порядка аппроксимирующего полинома - при использовании метода Ритца.