Относительная погрешность обычно выражается в процентах и дает наиболее ясное представление о погрешности, поскольку характеризует соотношение между абсолютной погрешностью и истинной величиной:
δ = (Δ / Х) × 100 % (5.2)
Следует заметить, что точное значение Х заранее неизвестно, поэтому погрешности измерений могут оцениваться только приближенно.
Чтобы повысить точность и достоверность измерений необходимо уменьшить погрешности, которые возникают вследствие несовершенства методов и средств измерений, недостатков проведения опыта, влияния различных внешних факторов, субъективных особенностей экспериментатора.
Погрешности классифицируются на систематические и случайные. Систематические погрешности остаются постоянными при повторных экспериментах или изменяются по определенному закону. Их разделяют на пять групп:
– инструментальные погрешности;
– погрешности из-за неправильной установки;
– погрешности в результате действия внешней среды (температуры, магнитных и электрических полей, атмосферного давления, влажности, вибрации и колебаний);
– субъективные погрешности;
– погрешности метода.
Систематические погрешности необходимо обязательно исключить, так как они могут привести к неправильным научным выводам. Они могут быть устранены следующими методами:
– путем регулирования средств измерений, тщательной их поверки, устранения внешних воздействий;
– исключения погрешности в процессе эксперимента путем повторного измерения;
– путем нахождения погрешности с помощью более точного средства измерения и её учета.
Если систематическую погрешность устранить нельзя, то ограничиваются оценкой её границ.
Случайными называют погрешности, которые возникают случайно и не могут быть исключены. Однако при наличии многократных повторений наиболее отклоняющиеся измерения можно исключить с помощью статистических методов. Разновидностью случайных погрешностей являются грубые погрешности или промахи. Наиболее типичными причинами промахов являются ошибки при наблюдениях: неправильный отсчет, описки при записи результатов, различные манипуляции с приборами.
Измерительные приборы также характеризуются погрешностью и точностью, стабильностью измерений и чувствительностью. Под абсолютной погрешностью прибора понимают величину:
b = ± (х – хд), (5.3)
где х – показание прибора;
хд – действительное значение измеряемой величины, определяемое более точным методом.
Часто для оценки погрешности приборов применяют относительную погрешность в процентах:
bот = ± ((х – хд) / хд) · 100%. (5.4)
Погрешность прибора является важнейшей его характеристикой. Она возникает вследствие некачественного изготовления или неудовлетворительной эксплуатации, что приводит к систематическим погрешностям. Кроме них, возникают и случайные погрешности, обусловленные сочетанием различных факторов. Поэтому основными характеристиками прибора являются суммарные погрешности, определяющие его точность. В зависимости от величины допускаемых погрешностей приборы делятся на классы точности: 1-й – наивысший, 4-й – наинизший.
Разность между максимальным и минимальным показателями прибора называют размахом. Если эта величина непостоянная при прямом и обратном ходах, то эту разность называют вариацией показаний. Под чувствительностью прибора понимают способность отсчитывающего устройства реагировать на изменения измеряемой величины, а под стабильностью – свойства отсчетного устройства обеспечивать постоянство показаний одной и той же величины. Стабильность прибора определяется вариацией показаний.
Все средства измерений должны проходить периодическую поверку, которая может быть государственной, ведомственной и рабочей, проводимой перед началом измерений. Наиболее распространенным способом поверки прибора является его сопоставление с образцовым прибором.
Методы оценки измерений. Общая погрешность измерений в основном определяется случайной погрешностью, учет которой очень важен.Анализ случайных погрешностей основывается на теории случайных ошибок. В основе теории случайных ошибок лежит предположение о том, что при большом числе измерений случайные погрешности одинаковой величины, но разного знака, встречаются одинаково часто. Большие погрешности встречаются реже, чем малые, или вероятность появления погрешности уменьшается с ростом её величины. При бесконечно большом числе измерений истинное значение измеряемой величины равно среднеарифметическому значению всех результатов измерений, а появление того или иного результата как случайного события описывается нормальным законом распределения.
Различают генеральную и выборочную совокупность измерений. Совокупность всех возможных значений случайной величины в рассматриваемых условиях представляет собой генеральную совокупность. Некоторая часть этих экспериментов, которая имеет место в действительных условиях, является выборочной или выборкой. Число экспериментов, составляющих выборку, представляет её объем. Обычно считают, если число измерений n > 30, то среднее значение данной совокупности х приближается к его истинному значению.
Теория случайных ошибок позволяет решить две основные задачи: оценить точность и надежность измерения при данном количестве замеров; определить минимальное количество замеров, гарантирующее требуемую точность и надежность измерения. Наряду с этим возникает часто необходимость исключить грубые ошибки, определить достоверность полученных данных и др.
Интервальная оценка с помощью доверительной вероятности. Для большой выборки и нормального закона распределения характеристикой измерения являются дисперсия Д или коэффициент вариации:
Д = s2 = 
; k в = s / 
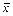. (5.5)
Дисперсия характеризует однородность измерения. Чем она выше, тем больше разброс. Коэффициент вариации характеризует изменчивость. Чем выше k в, тем больше изменчивость измерений относительно средних значений. Коэффициент вариации оценивает также разброс при оценке нескольких выборок.
Доверительным называется интервал значений хi, в который попадает истинное значение хд измеряемой величины с заданной вероятностью. Доверительной вероятностью измерения называют вероятность Рд того, что значение хд измеряемой величины попадет в данный доверительный интервал. Эта величина определяется в долях единицы или в процентах.
Пусть необходимо установить вероятность того, что хд попадет в диапазон а ≤ хд ≤ b. Доверительная вероятность Рд описывается выражением
Р д = Р (а < m (х) < b) = ½ (Ф ((b – х) / s) – Ф ((а – х) / s))),
где Ф (t) – функция Лапласса, аргументом которой является
t = m / s, (5.6)
здесь m = b – х; m = – (а – х),
t – гарантийный коэффициент.
Функция Лапласса Ф (t) является интегральной, ее численные значения Ф (t) табулированы и изменяются (при t от 0 до t = 4,0) соответственно в пределах Ф (t)=0 до Ф (t)=0,9999.
Возможна и иная задача. На основе установленной доверительной вероятности (очень часто ее принимают равной 0,9; 0,95) необходимо установить точность измерений, т.е. доверительный интервал 2 m.
Поскольку Рд = Ф (m / s), то по таблице обратным интерполированием можно определить половину доверительного интервала:
m = s · arg Ф (Рд) = s t. (5.7)
где t = arg Ф (Рд) – аргумент функции Лапласса или при малом числе измерений (n < 10) аргумент функции Стьюдента, которая также табулирована в зависимости от числа измерений n и вероятности Рд.
Доверительный интервал характеризует точность измерения данной выборки, а доверительная вероятность – достоверность измерения.
Установление минимального количества измерений. Задача сводится к установлению минимального объема выборки (числа измерений) Nmin при заданных значениях доверительного интервала 2 m и доверительной вероятности Рд. Пи выполнении измерений необходимо знать их точность Δ, которую обычно характеризуют с помощью среднего значения среднеквадратичного отклонения s0:
где 
. (5.8)
Значение s0 также называют средней ошибкой. Доверительный интервал ошибки измерения Δ определяется аналогично тому, как и для измерений 
. Зная t, по таблице легко определить доверительную вероятность ошибки измерения.
Часто возникает необходимость в определении минимального количества измерений по заданной точности и доверительной вероятности. В этом случае аналогично выражению (5.7) и с учетом условия (5.8) запишем
. (5.9)
Отсюда, полагая Nmin = n, имеем
(5.10)
где kв – коэффициент вариации, %;
Δ – точность измерения, %.
Параметр Nmin вычисляется в следующей последовательности:
– проводят предварительный эксперимент с количеством измерений n, которое составляет в зависимости от трудоемкости опыта от 20 до 50;
– вычисляют среднеквадратичное отклонение 
– в соответствии с поставленными задачами эксперимента устанавливают требуемую точность измерений (m, Δ), которая должна быть не менее точности прибора;
– устанавливают нормированное отклонение t, которое также задают в зависимости от точности измерений, например, при большей точности t =3,0, при малой – t= 2,0;
– из выражений (5.9) и (5.10) определяют Nmin. В дальнейшем в процессе эксперимента число измерений не должно быть меньше Nmin.
Оценки измерений с помощью σ и σ0 по приведенным методам справедливы при n >30. Для нахождения границ доверительного интервала при малых выборках применяют метод, предложенный в английским математиком В.С. Госсетом (псевдоним Стьюдент). Кривые распределения Стьюдента в случае 
(практически при n >20) переходят в кривые нормального распределения.
Для малой выборки доверительный интервал
(5.11)
где 
– коэффициент Стьюдента, принимаемый по таблице в зависимости от значения доверительной вероятности Фст.
Зная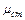 
, можно вычислить действительное значение изучаемой величины для малой выборки:
. (5.12)
Возможна иная постановка задачи. Пусть известны n известных измерений малой выборки. Необходимо определить доверительную вероятность Рд при условии, что погрешность среднего значения не выйдет за пределы 
. Задачу решают в такой последовательности. Вначале вычисляют 
, 
и , а затем, с помощью величины , известного n и таблицы определяют доверительную вероятность.
Исключение грубых ошибок. Появление этих ошибок ощутимо влияет на результат измерений. При анализе эксперимента необходимо, прежде всего, исключить грубые ошибки. Однако, до того как исключить то или иное измерение, необходимо убедиться, что это действительно грубая ошибка.
Известно несколько методов определения грубых ошибок статистического ряда. Наиболее простым способом исключения из ряда резко выделяющегося измерения является правило трех сигм, поскольку разброс случайных величин от среднего значения не превышает
(5.13)
Более достоверными являются методы, базирующиеся на использовании доверительного интервала. Пусть имеется статистический ряд малой выборки, подчиняющиеся закону нормального распределения. При наличии грубых ошибок критерии их появления вычисляют по формулам
, (5.14)
где 
, 
– наибольшее и наименьшее значения из n измерений.
Установленные критерии сопоставляют с максимальным значением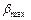 
, приведенным в таблице в зависимости от доверительной вероятности и числа измерений. После исключения грубых ошибок определяют новые значения и s.
Методика выявления грубых ошибок с использованием критерия В.И. Романовского сводится к следующему. Задаются доверительной вероятностью Рд, и по таблице в зависимости от n находится коэффициент q. Вычисляют предельно допустимую абсолютную ошибку отдельного измерения
. (5.15)
Если 
, измерение 
исключают из ряда наблюдений.
Для приближенной оценки можно применять такую методику:
– вычислить по (5.5) среднеквадратичное отклонение s;
– определить с помощью (5.8) среднюю ошибку s0;
– принять доверительную вероятность 
и найти доверительный интервал 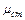из формулы (5.11);
– окончательно установить действительное значение измеряемой величины по формуле (5.12).
Определение ошибки функции. Во многих случаях в процессе экспериментальных исследований приходится иметь дело с косвенным измерениями. При этом неизбежно в расчетах применяют функциональные зависимости типа у = f (х 1, х 2, …, хn). Поскольку в данную функцию подставляют не истинные, а приближенные значения, то и окончательный результат также будет приближенным. В связи с этим одной из задач исследований является определение ошибки функции, если известны ошибки их аргументов.
При исследовании функции одного переменного предельные абсолютные 
и относительные 
ошибки (погрешности) вычисляют по формулам:
; (5.16)
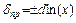, (5.17)
где 
– производная функции 
;
– дифференциал натурального логарифма функции.
Если исследуется функция многих переменных, то
; (5.18)
. (5.19)
В формулах (5.18) и (5.19) под знаком суммы и дифференциала понимают абсолютные величины. Порядок определения ошибок с помощью этих уравнений следующий:
– определяют абсолютные и относительные ошибки аргументов (независимых переменных). Обычно величина хд ± Δ каждого переменного измерена, следовательно, абсолютные ошибки для аргументов известны, т.е. 
, 
, …, 
;
– вычисляют относительные ошибки независимых переменных:
; 
, …, 
. (5.20)
– находят частные дифференциалы функции и по формуле (5.18) вычисляют Δ пр в размерностях функции и по f (y);
– вычисляют по (5.19) относительную погрешность , %.
ЛЕКЦИЯ 11
5.3 Рациональное планирование эксперимента
Основные понятия. Традиционный экспериментальный метод исследования заключается в установлении зависимости при изменении одного фактора и постоянстве остальных (однофакторный эксперимент). Этот метод обладает рядом существенных недостатков. Основным из них является не всегда корректное допущение о возможности стабилизации всех переменных исследуемого объекта при последовательном изучении каждого из них. Кроме того, такой подход обладает исключительной трудоемкостью. Более рационально планировать эксперимент с использованием методов математической статистики и теории вероятностей.
Под планированием экспериментальных исследований понимают математическое обоснование количества изучаемых проб (точек, объектов), последовательности измерений, числа влияющих факторов и уравнений их рассмотрения в зависимости от поставленной задачи с целью достижения максимальной информативности эксперимента, достоверности данных и получаемых зависимостей при минимальных затратах труда. Таким образом, рациональное планирование эксперимента преследует следующую основную цель: как провести эксперимент с минимальной трудоемкостью и наименьшим количеством измерений, получая при этом максимум достоверной информации.
В основу планирования эксперимента Р.А. Фишером (в 1925 году) был положен метод дисперсионного анализа и использование так называемого латинского квадрата. В наше время теория рационального планирования эксперимента включает несколько направлений, среди которых можно выделить:
– планирование многофакторного эксперимента на основе дисперсионного анализа;
– планирование экстремальных экспериментов;
– планирование отсеивающих экспериментов;
– планирование многофункциональных экспериментов на основе регрессионного анализа.
Методы рационального планирования эксперимента позволяют одновременно изучить влияние на исследуемый объект ряда факторов (многофакторный эксперимент). Они основаны на математической теории, которая определяет оптимальные условия эксперимента, в том числе и при неполном значении физической сущности явления. Для этого математические методы используют не только на стадии обработки результатов измерений, но также при подготовке и проведении опытов. Это позволяет с помощью эксперимента исследовать и оптимизировать сложные процессы и системы, обеспечивая высокую эффективность и точность определения исследуемых факторов.
При планировании экспериментальных исследований обычно предусматривается решение таких вопросов:
– определение величины и количества интервалов между экспериментальными точками;
– установление числа опытов при фиксированных параметрах на различных участках области изменения независимых переменных;
– разработку плана и последовательности проведения опытов.
Решение этих задач часто усложняется необходимостью учета ряда специфичных обстоятельств, связанных с используемой техникой, с сущностью явления и глубиной его изучения, с реальными возможностями постановки и проведения опытов. Однако в настоящее время установлены некоторые общие положения, которые необходимо соблюдать при рациональном планировании экспериментальных исследований. Так, например, теория математического планирования эксперимента основывается на ряде концепций, которые обеспечивают успешную реализацию задач исследования. К ним относятся концепции рандомизации, последовательного проведения эксперимента, математического моделирования, оптимального использования факторного пространства и ряд других.
Принцип рандомизации заключается в том, что в план эксперимента вводят элемент случайности. Для этого эксперимент составляют так, чтобы факторы, трудно поддающиеся контролю, учитывать статистически и исключать как систематические ошибки.
При последовательном проведении эксперимента его выполняют поэтапно, а результаты каждого этапа анализируют и принимают решение о целесообразности проведения дальнейших исследований (рис. 5.1). В результате эксперимента получают уравнение регрессии, которое называют математической моделью процесса. Под моделью понимают не абсолютно точное описание явления (подобно закону), а приближенное выражение
 |
, которое удовлетворительно характеризует явление в некоторой локальной области факторного пространства. Для описания одного и того же явления можно предложить несколько моделей, оценка которых производится по критерию Фишера. Так как степень полинома, адекватно описывающего процесс, предсказать невозможно, то сначала пытаются описать явление линейной моделью, а затем (если она неадекватна) повышают степень полинома, т.е. проводят эксперимент поэтапно.
Оптимальное использование факторного пространства заключается в том, что состояние объекта в каждом опыте определяется по результату одновременного оптимального варьирования n – факторов в m – мерном пространстве. Это позволяет добиться значительного увеличения точности расчета коэффициентов полученной модели и уменьшения трудоемкости эксперимента.
Классические и факторные планы проведения экспериментальных исследований. При планировании экспериментальных исследований, прежде всего, необходимо установить число независимых переменных, влияющих на изучаемый параметр. Обычно число независимых переменных равно 3, 4, 5 и более. Планирование таких многофакторных экспериментов осуществляется с использованием классических и факторных планов.
Классический план можно считать универсальным, так как его применяют при любых экспериментальных исследованиях. Факторный план является более точным и менее трудоемким, однако он ограничивается изучением определенных процессов и явлений, поэтому имеет ограниченное применение.
Рассмотрим подробнее эти планы. При классическом планировании эксперимента все независимые переменные, кроме одной, например Х, фиксируются, а переменная Х варьируется во всем диапазоне изменения. Затем задаются новые значения независимым переменным Y, Z, и вновь варьируется Х и т.д. Если число интервалов равно р, то в этом случае необходимо сделать опыты на 
уровнях (здесь k –число опытов при всех фиксированных параметрах на одном уровне).
Если известно, что зависимая переменная W является той или иной функцией независимых переменных, то объем эксперимента удается немного сократить. Например, если
, (5.21)
то можно сделать три группы исследований: в первой фиксируют какую-нибудь пару значений Y и Z, изменяя Х во всем интервале, что позволяет определить константы а и n; во второй – фиксируют какие-либо значения Х и Z, изменяя Y во всем диапазоне, что позволяет установить b и k, в третьем – фиксируют какие-либо значения Х и Y, изменяя Z во всем интервале, и определяя с и m.
Факторные планы применяют тогда, когда независимая функция W имеет вид
; (5.22)
. (5.23)
В последнем случае путем логарифмирования выражения (5.23) можно получить
. (5.24)
Вводя обозначения ξ = 
; j 1(х)= 
; j 2(Y)= 
; j 3(Z)= 
, получим
ξ = j 1(X)+ j 2(Y)+ j 3(Z). (5.25)
Чаще всего приходится иметь дело с экспериментальным изучением парных зависимостей между первичным фактором (аргументом) и вторичным фактором. Последовательность операций при однофакторном анализе проиллюстрируем на примере экспериментальных взрывов в полевых выработках (табл. 5.1).
Таблица 5.1 – Зависимость удельного расхода ВВ (кг/м3) от
прочности пород на одноосное сжатие
| Номер опыта n | Прочность пород на одноосное сжатие σ с, МПа (уровни k) | ||||
| 3,1 3,2 4,3 2,7 4,1 | 3,9 3,7 4,2 4,3 4,0 | 4,2 4,3 4,9 4,0 4,5 | 4,9 5,1 5,0 5,2 4,8 | 5,3 5,4 5,1 5,0 4,9 | |
| Среднее | 3,48 | 4,02 | 4,38 | 5,00 | 5,14 |
Как видно из табл. 5.1, эксперимент выполнен на пяти уровнях (k = 5) прочности подрываемых пород, причем на каждом уровне измерения повторялись пять раз, т.е. n = 5.
Для определения значимости влияния прочности горных пород на удельный расход ВВ при проведении буровзрывных работ в полевых выработках сделаем такие расчеты:
а) определим сумму квадратов всех наблюдений:
;
б) определим среднюю сумму квадратов по столбцам:
;
в) определим средний квадрат общей суммы:
;
г) рассчитаем дисперсии 
и 
:
;
;
д) сравним дисперсии 
и 
по критерию Фишера, для чего используем так называемое распределение Фишера:
Полученное значение F сравним с квантилями распределения Фишера для степеней свободы 
и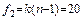 
. При уровне значимости 0,05 имеем F 0,95(4; 20)=2,9. Таким образом, F > 2,9, что подтверждает тот факт, что прочность горных пород при одноосном сжатии существенно влияет на удельный расход взрывчатых веществ при проведении взрывных работ в полевых выработках.
е) вычислим дисперсию принятого фактора по формуле:
Планирование многофакторного эксперимента. Обычно вторичный (функциональный) фактор является зависимым не от одного, а от нескольких факторов (аргументов). Чтобы выявить влияние каждого из них, необходимо задать ему не менее 4-5 различных значений. Однако при этом для полного исследования взаимного влияния нескольких факторов на один и тот же вторичный фактор будет необходимо очень большое число опытов. Например, для полного исследования четырех факторов, принимающих по 5 значений, необходимо провести 54 = 625 комбинаций опытов, не учитывая их повторения в идентичных условиях.
Такое большое количество экспериментов очень сложно провести, поэтому число опытов обычно сокращают за счет исследования лишь части наиболее существенных факторов; уменьшения количества значений и уровней каждого из факторов; исследования влияния каждого из факторов лишь при некоторых частных значениях других факторов.
Рассмотренный ранее пример однофакторного эксперимента включает в себя все возможные уровни факторов в диапазоне их изменения. Такой эксперимент называется полным факторным экспериментом. Число попыток при таком эксперименте равняется произведению уровней всех факторов (для трехфакторного – 53 = 125). Поэтому при большом числе факторов уместен дробный факторный эксперимент, при котором ряд сочетаний уровней пропускается, в результате чего число попыток уменьшатся.
Если проводится двухфакторный эксперимент на пяти уровнях для обоих факторов, то число опытов составит 25. Все сочетания факторов можно изобразить в виде соответствующего квадрата, где латинскими буквами А и В обозначены факторы (рис. 5.2). Индекс при этих буквах обозначает уровень исследуемого фактора. Такие квадраты Фишер назвал латинскими.
Необходимо иметь в виду, что к факторам А и В можно добавить третий фактор С, не меняя числа попыток. Однако при этом не все сочетания А, В, С будут присутствовать в квадрате. Если разместить уровни фактора С так, чтобы в каждой стороне и столбце встречались все его уровни, то, усредняя данные по строкам и рядкам, будем иметь средние, постоянные значения фактора С, что не должно исказить влияние факторов А и В на изучаемый параметр (рис. 5.2,б).
Далее можно добавить к этому плану еще и четвертый фактор, чтобы в каждой строке и каждом столбце такого плана были бы все пять уровней третьего и следующих факторов и одновременно не один уровень третьего и следующих факторов не встречались вместе по всей таблиц более одного раза. Таким образом, избежать большого объема экспериментальных исследований можно лишь в том случае, если спланировать сочетания различных факторов так, чтобы при минимальном числе опытов наиболее равномерно охватить всю площадь таблицы возможных сочетаний влияющих факторов.
Планирование экстремальных экспериментов. Наиболее широко используют планы экстремального эксперимента, позволяющие описать модель с помощью полинома и оптимизировать исследуемый объект. Эти планы представляют собой систему опытов, содержащую возможные неповторяющиеся комбинации выбранных факторов при заданных уровнях их варьирования. Метод позволяет изучать влияние многих факторов на исследуемый процесс в некоторой области факторного пространства, лежащего в окрестности выбранной точки с координатами (Z 01, Z 02,…, Z 0 n ). Полученный полином k -й степени (функция отклика) для математического описания процесса можно использовать также для его оптимизации, т.е. определять параметры, при которых явление или процесс будет протекать наиболее эффективно.
Экстремальный эксперимент основан на том, что исследуемую непрерывную функцию y = f (Z 1, Z 2,…, Zn), имеющую все производные в заданной точке с координатами Z 01, Z 02,…, Z 0 n , можно разложить в ряд Тейлора:
у = β 0+ β 1 Z 1+ β 2 Z 2 +…+ βnZn + β 12 Z 1 Z 2+…+
+β (n– 1) n Zn –1 Zn + β 11 Z 12+ β 22 Z 22+…+ βnnZn 2, (5.27)
где β 0 – значение функции отклика в начале координат Z 01, Z 02,…, Z 0 n ;
. (5.28)
Ряд Тейлора аналогичен уравнению регрессии:
у = а 0+ а 1 х 1+ а 2 х 2+…+ аnхn + а 12 х 1 х 2+…+
+ а ( n –1) nхn –1 х n+ а 11 
+ а 22 
+…+ аnn 
, (5.29)
где a 0, ai, aij, aii – коэффициенты регрессии;
хі – кодированная переменная, введенная в целях упрощения арифметических расчетов и равная
хi = (zi – z 0 i ) /∆ zi; ∆ zi = (zi max– zi min) / 2; z 0 i =(zi max+ zi min) / 2.
Следовательно, хi является относительной величиной, максимальному значению zi max соответствует хi =+1, а минимальному zi min соответствует хi =–1.
Коэффициенты регрессии уравнения (5.29) вычисляют методами математической статистики и представляют они собой приближенную оценку коэффициентов β 0, βi, βj и т.д. в уравнении (5.27), поэтому уравнение (5.29) описывает исследуемый объект только с определенной степенью точности.
Уравнение (5.29) широко используется для получения математической модели объектов исследования, хотя оно и не содержит информации о механизме явлений и его физико-химических свойствах. В математической теории эксперимента разработаны оптимальные планы получения уравнения типа (5.29). Определение коэффициентов регрессии и анализ уравнения производят с помощью ЭВМ.
Планы оптимального эксперимента реализуются в такой последовательности (рис. 5.1):
– оценка информации и определение n факторов, наиболее существенных для исследуемого процесса;
– использование математической модели в виде линейной функции отклика;
– анализ выбранной модели;
– нахождение экстремума в области n -мерного факторного пространства путем использования полинома k -й степени;
– если модель неадекватна, то в качестве модели выбирают полиномы более высокого порядка.
Планирование экстремального эксперимента с целью описания исследуемого объекта. Планирование эксперимента начинается со сбора, изучения и анализа имеющих данных об объекте. В результате определяют выходной параметр у и входные – zi. Выходной параметр (переменная состояния объекта) должен иметь количественную характеристику, т.е. измеряться с достаточной степенью точности и однозначно характеризовать объект исследования. Входные параметры zi должны иметь границы изменения (zi max– zi min), причем при различных комбинациях факторов zi переменная состояния объекта у не должна выходить из области допустимых значений. Между фактором zi и значением у необходимо однозначное соответствие. Факторы zi между собой взаимно независимы. В целях упрощения вычислений удобно пользоваться относительными переменными хi, ∆ zi, z 0 i . Значениям zi max и zi min соответствуют хi =+1 и хi =–1.
Среди планов экстремального эксперимента наиболее простыми являются планы полного факторного эксперимента (ПФЭ), в случае реализации которых определяется значение параметров состояния объекта у при всех возможных сочетаниях уровней варьирования факторов zi. Если мы имеем дело с n -факторами, каждый из которых устанавливается на q уровнях, то для того, чтобы осуществить полный факторный эксперимент, необходимо поставить m = qn опытов. С увеличением q резко возрастает количество опытов, поэтому, если q > 2, планы ПФЭ редко используются. Наибольшее распространение получили планы типа 2 n.
Рассмотрим пример. Допустим, что необходимо исследовать явление в зависимости от изменения двух факторов z 1 и z 2 методом полного двухфакторного эксперимента. Предположим, что явление описывается линейным полиномом, т.е. поверхность отклика представляет собой плоскость, характеризуемую полиномом
у = а 0 + а 1 х 1 + а 2 х 2. (5.30)
Чтобы построить поверхность отклика в виде плоскости, достаточно провести четыре опыта. Наиболее удобно выбранные факторы варьировать на верхнем и нижнем уровнях, что соответствует хi = +1 и х i = –1. Для удобства планирования эксперимента составляют план-матрицу (таб