Пример 1.1. Графическим методом определить оптимальное сочетание посевов картофеля и кукурузы. Исходные данные приведены в таблице 1.
Исходные данные задачи
Таблица 1
| Показатели | Картофель | Кукуруза | Объем производственных ресурсов |
| Площадь орошаемой земли, га | 0,1 | 0,2 | |
| Трудовые ресурсы чел/дн. | |||
| Цена продуктов руб. | - |
Критерий оптимальности - максимум денежных поступлений от реализации продукции.
Решение. Задача состоит в том, чтобы при данных нормативах затрат производственных ресурсов и их объемов определить, сколько надо производить картофеля и кукурузы, чтобы получить максимум выручки от peaлизации продукции. Поэтому для составления математической модели обозначим через: 
тонн - количество картофеля, 
тонн - количество кукурузы, которое надо производить в хозяйстве при данных условиях. Составим ограничение по площади орошаемой земли. На одну тонну картофеля требуется 0,1га, следовательно на тонн потребуется0,1 га земли. Аналогично, на тонн кукурузы требуется 0,2 га земли. Под эти культуры отведено 22 га, поэтому должно выполнятся неравенство
(1.1)
Из таких же соображений запишем неравенство по использованию трудовых ресурсов:
(1.2)
Целевая функция - выручка от реализации продукции:
(1.3)
Таким образом, модель задачи имеет вид:
(1.4)
(1.5)
Для удобства обе части первого неравенства мы умножили на 10, а второго разделили на 4. Мы получили стандартную задачу линейного программирования.
Вместо неравенств системы (1.4) запишем строгие равенства и построим эти прямые. Из уравнения 
, при
Нанесем точки А и В на график и проведем через них прямую АВ. Для уравнения
Построим прямую CD.
Теперь вновь обратимся к неравенствам (1.4). Прямая АВ, соответствующая первому неравенству, разбивает плоскость на две полуплоскости. Какая из них отвечает первому неравенству системы (1.4)? Существует простое правило: если коэффициент перед больше нуля и неравенство вида 
, то такому неравенству отвечает левая полуплоскость, если неравенство 
, то правая. Заметим, что если коэффициент перед меньше нуля, то его можно сделать положительным, умножив обе 
части неравенства на 
и поменяв знак неравенства на противоположный.
В нашем примере обеим неравенствам системы (1.4) отвечают левые полуплоскости, отмеченные штриховкой на рис 1.1. Пересечение этих полуплоскостей, лежащих в первой четверти, дает четырехугольник OAMD. Этот четырехугольник - область допустимых значений , . В этой области надо искать оптимальное решение.
Теперь обратимся к целевой функции (1.5). Построим вектор 
, координатами которого являются коэффициенты: 
. Вектор показывает направление наибольшего возрастания функции . Значит, чем дальше мы возьмем точку, лежащую в области OAMD в направлении вектора 
, тем большее значение получим. В этом и состоит геометрическая интерпретация задачи (1.4) - (1.5) - найти точку, лежащую в области OAMD наиболее удаленную в направлении вектора .
Практически для определения этой точки проводят прямую N, перпендикулярную и мысленно сдвигают ее параллельно самой себе в направлении , наблюдая, через какую точку мы выйдем из области OAMD (точку касания прямой и OAMD) в данном случае это точка М.
Ее координаты дают оптимальное решение. Для определения координат точки М решаем систему уравнений АВ и CD, пересечением которых является М:
Вычитая из второго уравнения первое, получим 
, откуда
, следовательно 
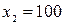. Подставляя эти значения в (1.5), находим, что
Ответ: если произвести 20 тонн картофеля и 100 тонн кукурузы, т. е. занять 2 га под картофель и 20 га под кукурузу, то будет получена наибольшая выручка в 9100 руб.
Метод решения, изложенный в этом параграфе, называется графическим методом линейного программирования.
Замечание 1. Графический метод удобно применять в случае двух переменных. Если число переменных больше или равно трем, обычно применяется симплексный метод (разделы 2, 3). Но есть один частный
случай, когда можно воспользоваться графическим методом. Графический метод можно применять в случае, когда число неизвестных
равно 
где 
- число уравнений системы ограничений. Рассмотрим соответствующий пример.
Пример 1.2. 
(1.6)
(1.7)
Решение. В системе ограничений 4 уравнения и 6 неизвестных. Выберем 4 переменные (по количеству уравнений) 
и выразим их через остальные переменные, т. е. через 
(1.8)
Целевую функцию 
также выразим через 
подставляя в формулу (1.6) выражения из формул (1.8):
Отсюда, после приведения подобных членов, получим
(1.9)
Переменные в (1.8) должны быть неотрицательны при любых значениях 
, согласно условиям (1.7). Поэтому
(1.10)
(1.11)
Таким образом, задача (1.6) - (1.7) сводится к задаче (1.10) - (1.11) с двумя переменными.
Решим задачу (1.10) - (1.11) графическим методом. В плоскости 
построим область, соответствующую системе неравенств (1.10) и вектор (1, 1) См. рис. 1.2. Очевидно, максимум функции L находится в точке R. 
Решая систему уравнений
находим координаты точки R:
(1.12)
Как видно из рис. 1.2, в точке R 
Осталось найти значения переменных 
Это можно сделать, подставив найденные значения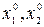 
(1.12) в выражения для 
из формул (1.10)
Максимальное значение целевой функции вычислим, подставляя значения 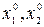из формул (1.12) в формулу (1.11):
Замечание 2. Запишем матрицу коэффициентов при неизвестных системы ограничений (1.7):
(1.13)
Эта матрица содержит единичную матрицу коэффициентов при 
В общем случае матриц системы ограничений с помощью элементарных преобразований следует преобразовать к виду, аналогичному (1.13) и только после этого применять метод решения, описанный в примере 1.2.
Идея симплекс-метода
Идею симплекс-метода разберем на простом примере:
(2.1)
(2.2)
Во-первых, среди переменных 
надо выбрать три переменные (по количеству ограничений (2.1)), которые из уравнений (2.1) легко выражаются через остальные переменные. Из (2.1) видно, что переменные 
можно выразить через 
. Говорят, что - свободные переменные. Из (2.1) находим:
(2.1’)
Функция F также должна быть выражена через свободные переменные. Поскольку в формуле (2.2) F уже выражена через , никаких дополнительных преобразований не требуется.
Так как все переменные должны быть неотрицательны, то наименьшее возможное значение переменных , это значение 
. При этих значениях свободных переменных несвободные (базисные) переменные окажутся равными 
. (Из (2.1’) при ). Совокупность значений
(2.3)
удовлетворяет всем ограничениям (2.1). При этом F = 3. (Из формулы (2.2) при ). Набор значений неизвестных (2.3) называется опорным решением задачи (2.1)-(2.2).
Посмотрим нельзя ли за счет увеличения значения 
или 
добиться уменьшения функции. Напомним, что по условию (2.2) 
. Из формулы (2.2) видно, что поскольку входит в (2.2) со знаком плюс, то ее увеличение приведет к увеличению F. Это нам не выгодно. Переменная входит в (2.2) со знаком минус. Поэтому ее увеличение приведет к уменьшению F. Чем больше мы увеличим тем меньшее значение примет F. Но изменение переменной вызовет изменение базисных переменных 
по формулам (2.1). Эти изменения могут оказаться такими, что базисные переменные станут отрицательными, а этого не должно быть по условию. Рассмотрим систему (2.1’). Из первого уравнения видно, что если 
а увеличивается, начиная от значения 
, то условие 
приводит к неравенству 
Второе уравнение в (2.1) и условие 
дают неравенство 
Третье уравнение приводит к неравенству 
, которое выполняется при любых 
Решая систему неравенств
находим, что 
. Следовательно, переменную можно увеличить до значения 
. Подставляя 
в (2.1) получим, что
(2.4)
Из формулы (2.2) при 
т. е. мы добились уменьшения значения F.
Теперь за свободные переменные примем и , т.е. те переменные, значения которых в (2.4) равны нулю. Выразим базисные переменные 
через свободные 
, пользуясь формулами (2.1). Из первого уравнения
Подставляя это выражение во второе и третье уравнения, получим:
Функцию F также надо выразить через свободные переменные:
Задачу (2.1), (2.2) мы преобразовали к виду:
(2.5)
(2.6)
Проведем для системы (2.5) такое же рассуждение, как для (2.1), (2.2). Рассмотрим формулу (2.6). Мы видим, что увеличение переменных от значений 
приводит лишь к увеличению функции F, поэтому дальнейшее уменьшение значения F невозможно. Следовательно, решение (2.4) является искомым решением. В этой точке функция F принимает наименьшее значение Fmin = 1.