Основным методом решения задач линейного программирования является симплексный метод. На практике преобразования системы уравнений, проводятся в специальных таблицах, называемых симплексными. Это более удобно для решения задач на ЭВМ. Правила вычислений с помощью этих таблиц рассмотрим на следующем примере.
Пример 3.1. Найти наибольшее значение линейной функции
(3.1)
при следующих ограничениях на переменные:
(3.2)
Решение. Сначала систему ограничений (3.2) необходимо привести к каноническому виду. Для этого вводят дополнительные
переменные, которые прибавляют к левой части каждого из неравенств (3.2). После этого преобразованная система (3.2) будет иметь
вид:
(3.2’)
Примем за базисные переменные дополнительные переменные 
. Тогда свободными переменными будут 
, т. е. все остальные переменные. Целевая функция z должна быть выражена через свободные переменные. В нашем примере функция z уже выражена через , поэтому она не требует дополнительных преобразований.
Итак, предварительные преобразования задачи состоят в том, чтобы систему ограничений преобразовать с помощью введения дополнительных переменных в систему уравнений, принять за базисные переменные дополнительные переменные, выразить целевую функцию z через свободные переменные.
После этого заполняется первая симплексная таблица.
Таблица 3.1
Первая симплексная таблица
| БП | СЧ | 
| 
| 
| 
| 
| 
| 
|
|
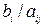
| 9.5 | |||||||
|
| 6.5 | |||||||
|
| - | |||||||
|  3
| |||||||
| С | -7 | -5 | - |
В первую таблицу заносят исходные данные задачи, содержащиеся в системе (3.2') и уравнении (3.1). В табл. 3.1 приняты следующие обозначения: БП - базисные переменные. В этот столбец заносятся переменные 
, которые мы приняли за базисные. СЧ - свободные члены. В столбец СЧ заносят правые части уравнения (3.2'). Далее идет перечень всех переменных 
. В столбец , записывают коэффициенты, стоящие перед в уравнениях системы (3.2'). В третьем уравнении (3.2'). | отсутствует, т. е. коэффициент перед , равен нулю. Аналогично, в столбцы переменных 
заносят коэффициенты при этих переменных из системы (3.2'). Осталось объяснить, как заполняется последняя строка С. Эта строка отводится для коэффициентовцелевой функции z (см. 3.1). В столбец СЧ записывают свободный член (т.е. постоянное слагаемое) функции z. В данном случае он равен нулю. В столбцы заносят соответствующие коэффициенты с противоположными знаками. Коэффициент при равен 7, поэтому в табл.3.1 записывается -7. Таблица 3.1 заполнена.
В таблице 3.1 содержится решение задачи (3.1) - (3.2):
х3= 19, х4= 13, х5= 15, х6=18, х1 = 0, х2 = 0. (3.3)
Решение (3.3) называется опорным решением. Посмотрим, нельзя ли улучшить решение (3.3), т. е. нельзя ли, изменяя значения переменных 
, увеличить значение функции z (пока z = 0). Рассмотрим последнюю строку табл. 3.1, Она содержит отрицательные числа в столбцах 
. Это признак неоптимальности решения (3.3). Его можно улучшить. Для перехода к следующему улучшенному решению в табл. 3.1 выбирают разрешающий столбец и разрешающую сроку.
За разрешающий столбец принимается тот, который в последний строке С имеет наибольшее по абсолютной величине отрицательное число. (Среди других отрицательных чисел строки С). В табл. 3.1 это столбец . Он отмечается стрелкой. После этого определяется разрешающая строка. Для ее определения составляют отношения свободных членов табл. 3.1 к соответствующим положительным элементам разрешающего столбца (): 19:2 = 9,5; 13: 2 = 6,5; 18:3 = 6.
За разрешающую строку принимается та, которая имеет наименьшее такое отношение. В табл. 3.1 эта строка х6. Она также отмечена стрелкой. Эти отношения записывают в последний столбец табл. 3.1. Элемент, стоящий на пересечении разрешающей строки и разрешающего столбца называется разрешающим элементом. В табл. 3.1 он равен трем.
Теперь мы подготовились к тому, чтобы заполнить вторую симплексную таблицу, содержащую улучшенное решение. Во-первых, в табл. 3.2 изменяется состав базисных переменных. Из столбца БП надо вывести переменную 
, а на ее место поставить . На это указывают стрелки в табл. 3.1.
Вторая симплексная таблица (промежуточный этап заполнения)
Таблица 3.2а
| БП | СЧ |
|
|
|
|
|
|
|
|
| ||||||||
| ||||||||
|
| ||||||||
|
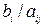
| 1/3 | |||||||
| С |
В первую очередь табл. 3.2 заполняется строка , которая в табл. 3.1 была разрешающей. Поэтому она называется начальной строкой. Для ее заполнения все элементы разрешающей строки х6 табл. 3.1
делят на разрешающий элемент 3 и результаты записывают в соответствующие столбцы строки x1 табл. 3.2:
18:3 = 6; 3: 3 = 1; 0: 3 = 0;..., 1: 3 = 1/3.
После этого заполняется тот столбец табл. 3.2, который был разрешающим в табл. 3.1. В данном случае это столбец . Во всех строках этого столбца (кроме строки где уже стоит единица), пишут нули (см. табл. 3.2а).
Остальные элементы табл. 3.2 вычисляются по правилу прямоугольника.
Вторая симплексная таблица
Таблица 3.2
| БП | СЧ |
|
|
|
|
|
|
|
|
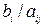
| -2/3 | 7/3 | ||||||
|  1
| -2/3 | ||||||
|
| ||||||||
|
| 1/3 | - | ||||||
| С | -5 | 7/3 | - |
Вычислим, например, элемент табл. 3.2, стоящий в столбце СЧ строки 
.
В табл. 3.1 рассмотрим элемент, стоящий на такой же позиции – он равен 19.
Мысленно построим прямоугольник, в одной вершине которого стоит число 19, в другой - разрешающий элемент (число 3), а две другие вершины отмечены в табл. 3.1 кружками. Искомый элемент табл. 3.2 равен произведению элементов, стоящих на главной диагонали прямоугольника 
минус произведение элементов на второй диагонали 
; разность надо разделить на разрешающий элемент:
.
Элемент столбца СЧ строки х4 табл. 3.2 вычисляется по формуле
.
Элемент столбца СЧ строки х5:
.
Наконец, элемент строки С столбца СЧ равен:
Аналогично, с помощью построения прямоугольника в табл. 3.1 в одной из вершин которого всегда находится разрешающий элемент, находят остальные коэффициенты табл. 3.2.
Например, x32 - элемент строки х3 столбца х2 вычисляется по формуле (см. табл.3.1):
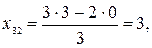
Так заполняется вся таблица 3.2. Решение, содержащееся в этой таблице неоптимально, т. к. в строке С есть отрицательное число - 5. Следовательно это решение можно улучшить. Перейдем к построению таблицы 3.3. Все выкладки, проведенные нами для перехода к таблице 3.2 повторяются, начиная с нахождения разрешающего столбца и разрешающей строки. Разрешающим столбцом в таблице 3.2 является столбец х2. Составим отношения СЧ к элементам столбца х2:7:3=7/3;1:1=1;15: 3 = 5. Наименьшее отношение дает строка х4 - она и является разрешающей. Разрешающий элемент: 1.
Третья симплексная таблица
Таблица 3.3
| БП | СЧ |
|
|
|
|
|
|
|
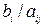
| -3 | 4/3 | ||||||
|
| -2/3 | - | ||||||
|
| -3 | |||||||
|
| 1/3 | |||||||
| С |  -1
| - |
Базисными переменными в таблице 3.3 являются х3, х2, х5, x1. Вначале заполняется строка х2 (начальная), которая получается из строки x4 табл. 3.2 делением на разрешающий элемент. Т.к. разрешающий элемент равен 1, строка x4 просто переписывается в табл. 3.3.
Затем в столбце х2 (бывшем разрешающем) пишем нули. Остальные элементы табл. 3.3 находим по правилу прямоугольника с помощью табл. 3.2. Решение, содержащееся в табл. 3.3 - неоптимально, т. к. в последней строке в столбце х6 есть отрицательное число - 1. Еще раз применяя алгоритм симплекс-метода, получаем оптимальное решение.
Четвертая симплексная таблица
Таблица 3.4
| БП | СЧ |
|
|
|
|
|
| |
|
| 3/4 | -9/4 | ||||||
|
| 1/2 | -1/2 | ||||||
|
| -3/2 | 3/2 | ||||||
|
| -1/4 | 3/4 | ||||||
| С | 3/4 | 11/4 |
Запишем оптимальное решение, содержащееся в табл. 3.4. Базисные
переменные равны свободным членам, т. е. 
, а свободные переменные (те, которых нет в столбце БП) равны нулю: 
. Элемент столбца СЧ строки С дает максимальное значение функции z: zmax = 50.
Замечание. Если задача решается на минимум целевой функции: то разрешающий столбец выбирается по наибольшему положительному числу последней строки. Признаком неоптимальности является наличие положительных чисел в последней строке. Остальные правила алгоритма не меняются.