Задача 8.1.1 На складах I, II, III хранится мука в следующих количествах: 90 т, 70 т, 50 т; эту муку надо перевезти в магазины 1, 2, 3, 4, потребности которых в муке равны: 80 т, 60 т, 40 т, 30 т. Стоимость перевозки 1 т муки в магазины 1, 2, 3, 4 со склада I равна соответственно 2, 1, 3, 2 руб.; со склада II -2, 3, 3, 1 руб.; со склада III — 3, 3, 2, 1 руб.
Надо определить такой план перевозок, чтобы транспортные расходы были минимальными.
Решение. I. Математическая модель. Обозначив через xij объем перевозки в тоннах из i- го склада в j -й магазин, получим систему ограничений данной задачи:
 (8.1.1)
(8.1.1)
Целевая функция  такова:
такова:
 (8.1.2)
(8.1.2)
Требуется минимизировать f на множестве решений системы ограничений (1).
11. Метод решения транспортной задачи.
1. Прежде всего составляем задачу, двойственную данной. Для этого заполняем таблицу 8.1.1:
Таблица 8.1.1
| 3-ий план | |||||||||||||
| 2-ий план | |||||||||||||
| 1-ий план | |||||||||||||

| 
| 
| 
| 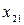
| 
| 
| 
| 
| 
| 
| 
| ||

| |||||||||||||

| |||||||||||||
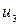
| |||||||||||||

| |||||||||||||

| |||||||||||||

| |||||||||||||

| |||||||||||||
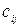
|
Система ограничений двойственной задачи такова:
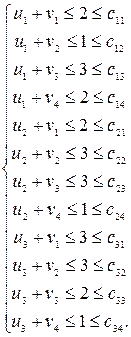 (8.1.3)
(8.1.3)
Выпишем целевую функцию двойственной задачи:
 (8.1.4)
(8.1.4)
Требуется максимизировать целевую функцию F на множестве решений системы ограничений (8.1.3).
2. Составление первоначального плана перевозок.
При составлении исходного плана перевозок удобно пользоваться приемом, известным под названием северо-западного угла. Этот прием заключается в следующем: сначала максимально возможное количество груза помещается в верхнюю левую клетку таблицы. В нашем случае  = 80, что полностью удовлетворяет потребность магазина 1. Затем заполняется соседняя клетка в первой строке, так как на складе I еще остается 10 т груза: х12 =10.
= 80, что полностью удовлетворяет потребность магазина 1. Затем заполняется соседняя клетка в первой строке, так как на складе I еще остается 10 т груза: х12 =10.
Переходим ко второй строке. Заполняем клетку II 2 (под клеткой 12). Значение x 22 определяется недостающими потребностями магазина 2: x22 = 50. Продолжаем этот процесс заполнения клеток таблицы, пока не будут удовлетворены все заказчики:
 (см. таблицу).
(см. таблицу).
Итак, первоначальный план поставок выглядит так:

При этом плане значение целевой функции есть:
 (руб.).
(руб.).
Заметим, что в этой задаче число заполненных мест равно 6.
Таблица 8.1.2
| I | |||||||||||||||||||
| II | |||||||||||||||||||
| III | |||||||||||||||||||
(В общем случае число занятых мест не больше  т - число поставщиков, п - число покупателей.)
т - число поставщиков, п - число покупателей.)
Итак, базис системы ограничений содержит  переменную. Следовательно, число клеток, заполненных положительными числами, не больше числа
переменную. Следовательно, число клеток, заполненных положительными числами, не больше числа  ; значения некоторых базисных переменных могут оказаться равными нулю.
; значения некоторых базисных переменных могут оказаться равными нулю.
3. Проверка полученного плана на оптимальность.
Используя сформулированные в предыдущей главе теоремы двойственности, можно вывести критерии для определения оптимальности получаемого очередного допустимого плана транспортной задачи.
Пусть мы получили некоторый допустимый план исходной задачи. Выпишем ограничения двойственной задачи, соответствующие ненулевым значениям переменных этого плана. Если рассматриваемый план исходной задачи является оптимальным, то эти ограничения должны выполняться как равенства при соответствующем решении двойственной задачи (теорема II). В таком случае получается система линейных уравнений, которая, как правило, имеет бесконечное множество решений. Находим одно из них:  Это решение подставляем в ограничения двойственной задачи, не вошедшие в систему уравнений. Если эти ограничения являются верными неравенствами при найденном решении, то проверяемый допустимый план исходной задачи является оптимальным. В противном случае - нет.
Это решение подставляем в ограничения двойственной задачи, не вошедшие в систему уравнений. Если эти ограничения являются верными неравенствами при найденном решении, то проверяемый допустимый план исходной задачи является оптимальным. В противном случае - нет.
Проследим рассмотренную последовательность шагов при проверке полученного плана (80, 10, 50, 20, 20, 30) на оптимальность. Числовые значения базисных переменных  запишем в таблице 8.1.1 над строкой переменных исходной задачи. Это облегчает выбор соответствующих ограничений двойственной задачи. В результате получаем систему ограничений из 6 уравнений с семью переменными:
запишем в таблице 8.1.1 над строкой переменных исходной задачи. Это облегчает выбор соответствующих ограничений двойственной задачи. В результате получаем систему ограничений из 6 уравнений с семью переменными:
 (8.1.5)
(8.1.5)
Найдем одно из решений этой системы, для чего одной из переменных (например, и1) придадим произвольное числовое значение (удобнее всего положить  равным 0):
равным 0):

Это решение удобно записать в виде вектора

Подставим найденные значения переменных двойственной задачи в остальные неравенства системы (8.1.3), не вошедшие в систему (8.1.5).
Выпишем сначала эти неравенства
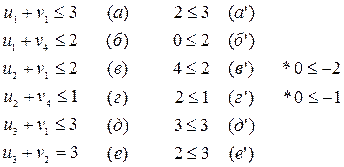 (8.1.6)
(8.1.6)
Из написанного видно, что неравенства (а'), (б'), (д'), (е') являются верными, а (в') и (г') – неверными, т. е. найденное решение системы (8.1.5) удовлетворяет не всем неравенствам системы ограничений (8.1.3). Следовательно, первоначальный план не является оптимальным.
4. Составление нового допустимого плана.
Перераспределив поставки, можно составить новый допустимый план. Очевидно, что при составлении нового плана придется использовать незанятые клетки. Заметим, что незанятых клеток в предыдущем плане осталось шесть. Какую из них следует занять? Заполняя одну из незанятых клеток, приходится одновременно изменять числа по меньшей мере в трех уже заполненных клетках, чтобы не нарушить итоговые значения в строках и столбцах таблицы. В связи с этим каждая свободная клетка при анализе возможностей улучшения плана не может рассматриваться изолированно, вне связи с несколькими уже занятыми клетками.
Анализ возможностей использования каждой незанятой клетки делается следующим образом. Для свободной клетки строится прямоугольный контур (цепь). Строится он так. Одна из вершин его находится в свободной клетке, а остальные – в занятых, причём все углы контура должны быть прямыми (см. рис. 8.1.1).

Рис. 8.1.1
В неверных равенствах (в') и (г') все члены переносим в правую часть. Выбираем неравенство, у которого правая часть имеет наименьшее значение. При этом выборе свободная клетка таблицы распределения, соответствующая этой переменной, оказывается наиболее перспективной из всех имеющихся свободных клеток для улучшения плана. В неравенствах (в') и (г') после переноса левых частей имеем:

Из чисел -2 и -1 выбираем наименьшее:  . Переменную
. Переменную  соответствующая неравенству (в), целесообразно включить в новый план (рис. 8.1.1).
соответствующая неравенству (в), целесообразно включить в новый план (рис. 8.1.1).
Данное перераспределение коснется только четырех клеток (I-1, I-2, II-1, II-2), являющихся вершинами квадрата. Итак, в клетку II-1 поместим число 50, это число прибавляем к 10, уже имеющемуся в клетке I-2, и вычитаем из чисел, стоящих в клетках с отрицательными знаками. Так приходим к новому варианту программы перевозок, приведенной в таблице 8.1.3
Таблица 8.1.3
| I | |||||||||||||||||||
| II | |||||||||||||||||||
| III | |||||||||||||||||||
Новый план уменьшает общую стоимость перевозок на 100 руб.
5. Проверка вновь полученного плана на оптимальность.
Значения переменных  записываем в таблицу над строкой значений первого лана. Получаем систему:
записываем в таблицу над строкой значений первого лана. Получаем систему:
 (8.1.7)
(8.1.7)
Находим одно из ее решений: (0; 0; —1; 2; 1; 3; 2). Подставим найденные значения переменных  в остальные неравенства системы (8.1.3), не вошедшие в систему (8.1.7):
в остальные неравенства системы (8.1.3), не вошедшие в систему (8.1.7):

Из полученных числовых неравенств одно неверное: 2  1. Следовательно, полученный второй план также не является оптимальным.
1. Следовательно, полученный второй план также не является оптимальным.
6. Переход к новому допустимому плану.
 Так как неравенству
Так как неравенству  соответствует переменная x24, то вводим переменную
соответствует переменная x24, то вводим переменную  24 в новый план. Для клетки II-4 строим цепь. На рисунке 8.1.2 эта цепь построена. В клетке II-4 поместим число 20, при этом числа клеток II-3, III-4 уменьшаем на 20, а число клетки II-4 увеличиваем на 20.
24 в новый план. Для клетки II-4 строим цепь. На рисунке 8.1.2 эта цепь построена. В клетке II-4 поместим число 20, при этом числа клеток II-3, III-4 уменьшаем на 20, а число клетки II-4 увеличиваем на 20.
|
Таблица 8.1.4
| I | |||||||||||||||||
| II | |||||||||||||||||
| III | |||||||||||||||||
7. Проверка третьего плана на оптимальность:
 (8.1.8)
(8.1.8)
(0; 0; 0; 2; 1; 2; 1) - одно из решений системы (8.1.8). Подставив значения  в неравенства, получим:
в неравенства, получим:

Все числовые неравенства верны. Следовательно, план x11 =30, x12 =60, x2 l= 50, х24 = 20, х33 = 40, х34 = 10 оптимальный.

 (руб.).
(руб.).
Вместе с решением данной задачи мы нашли решение и двойственной ей задачи. Решение двойственной задачи выглядит таким образом: 
 (руб.).
(руб.).
В дальнейшем мы будем находить Fmax для целевой функции двойственной задачи только для самоконтроля правильности решения.
III. Экономическая интерпретация полученного математического решения.
Итак, со склада I в магазин № 1 надо перевезти 30 т муки, в магазин 2 -60 т, со склада II в магазин 1- 50 т муки и в магазин 4- 20 т, а со склада III надо перевезти 40 т в магазин № 3 и 10 т в магазин 4.
Рассмотрим решение этой же задачи для случая, когда первоначальный опорный план составляется с помощью приема минимальной стоимости.
Таблица 8.1.5
| I | |||||||||||||||||
|  |
| |||||||||||||||
|
| ||||||||||||||||
1) Математическая модель задачи.

Целевая Функция имеет вид:

Задача двойственная данной может быть получена из таблицы 8.1.6:
Таблица 8.1.6
| 2 пл | - | - | - | - | - | - | |||||||
| 1пл | - | - | - | - | - | - | |||||||
 ~П
~D ~П
~D
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |

| |||||||||||||

| |||||||||||||
| |||||||||||||

| |||||||||||||

| |||||||||||||

| |||||||||||||

| |||||||||||||
|
Система ограничений двойственной задачи такова:
 (8.1.9.)
(8.1.9.)
Целевая функция двойственной задачи имеет вид:

Проверим 1-ый полученный опорный план, составленный по методу минимальной стоимости на оптимальность. Проследим рассмотренную последовательность шагов при проверке полученного плана (30, 60, 40, 30, 10, 40) на оптимальность. Числовые значения базисных переменных  запишем в таблицу 8.1.6 над строкой переменных исходной задачи. В результате получим систему ограничений из 6 уравнений с семью переменными.
запишем в таблицу 8.1.6 над строкой переменных исходной задачи. В результате получим систему ограничений из 6 уравнений с семью переменными.

Найдем одно из решений этой системы, для чего одной из переменной придадим произвольное числовое значение



Это решение запишем в виде вектора 
Подставим найденные значения переменных двойственной задачи в остальные неравенства системы (8.1.9).

Последнее неравенство является неверным. Следовательно, первоначальный план не является оптимальным. Очевидно, что при составлении нового плана придется использовать незанятую клетку III-4
Новый план представлен в таблице 8.1.7
Таблица 8.1.7
| I | |||||||||||||
| II | |||||||||||||
| III | |||||||||||||
Проверим вновь полученный план на оптимальность.
Значения переменных  записываем в таблицу над строкой значений первого плана. Получаем систему:
записываем в таблицу над строкой значений первого плана. Получаем систему:

Находим одно из решений при

Данное решение представим в виде вектора

Представим это решение в остальные неравенства системы ограничений двойственной задачи:

Все числовые неравенства верны. Следовательно, план  оптимальный
оптимальный
 (руб.).
(руб.).
Вместе с решением данной задачи мы нашли решение и двойственной ей задачи
 (руб.).
(руб.).
Итак, со склада I в магазин 1 надо перевести 30 т муки и в магазин 2-60 т, со склада II в магазин 1 -50 т муки и в магазин 4 -20 т, а со склада III в магазин 3 – 40 т и в магазин 4 – 10 т.
Задача 8.2.1. Имеется два склада и три потребителя. Надо составить наиболее выгодный план перевозок. Условие задачи представлено в следующей таблице:
Таблица 8.2.1
| Потребители Склады | Производство изделий в штуках | |||||||||
| I | 
| 
| 
| |||||||
| II | 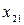
| 
| 
| |||||||
| Пропускная способность складов |
I. Математическая модель задачи. На множестве решений системы

найти минимальное значение функции

П. Задача, двойственная данной.
1)
Таблица 8.2.2
| 1-ый план | |||||||

| 
| 
| 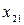
| 
| 
| ||

| |||||||

| |||||||

| |||||||

| |||||||

| |||||||
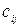
|

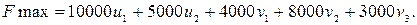
2) Определение первого плана.
Таблица 8.2.3
| I | ||||||||||||||
| II | ||||||||||||||

 (ед).
(ед).
3) Проверка полученного плана на оптимальность.

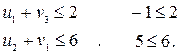
Следовательно, рассматриваемый план оптимален. Вычисляем значение целевой функции:
 (ед).
(ед).
III. Итак, всю продукцию первого склада следует распределить так: 4000 штук отправить 1-му потребителю, 6000 штук -
2-му потребителю. Продукцию склада II распределить между 2-м
и 3-м потребителями: 2000 штук - 2-му потребителю, 3000 штук-
3-му потребителю.
Задача 8.3.1. На вокзалы А и В прибыло по 30 комплектов мебели. Известно, что перевозка одного комплекта с вокзала А в магазины С, D, Е соответственно стоит 1 руб., 3 руб., 5 руб., а перевозка с вокзала В в те же магазины соответственно: 2 руб., 5 руб., 4 руб. Необходимо доставить по 20 комплектов мебели в каждый из магазинов. Составить план перевозок, минимальный по стоимости.
Решение.
I. Запишем условие задачи в виде таблицы:
Таблица 8.3.1
| Магазины Вокзалы | С | D | E | Прибыло мебели | ||||||
| A | 
| 
| 
| |||||||
| B | 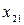
| 
| 
| |||||||
| Отправлено мебели |
Математическая формулировка такова: на множестве решений системы ограничений

найти минимальное значение целевой функции
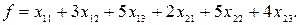
II. 1) Составим двойственную задачу:
Таблица 8.3.2
| 2 пл | |||||||
| 1пл | |||||||

| 
| 
| 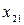
| 
| 
| ||

| |||||||

| |||||||

| |||||||

| |||||||

| |||||||
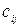
|
На множестве решений системы ограничений

найти максимальное значение целевой функции
2) Составим первый план:
Таблица 8.3.3
| С | D | E | ||||||||||||
| A | ||||||||||||||
| B | ||||||||||||||

 (руб.).
(руб.).
3) Проверим первый план на оптимальность. Базисным переменным соответствуют уравнения

Одно из решений этой системы: (0;2;1;3;2). Подставим это решение в остальные неравенства системы ограничений двойственной задачи  получим:
получим:  Отсюда следует, что первоначальное распределение не оптимальное.
Отсюда следует, что первоначальное распределение не оптимальное.
4) Составим новый план. Неравенству  соответствует переменная
соответствует переменная 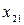 . Включим переменную
. Включим переменную 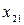 в базисные переменные при распределении поставок. Построим многокгольник для клетки переменной
в базисные переменные при распределении поставок. Построим многокгольник для клетки переменной 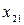 см. рис. 8.3.1
см. рис. 8.3.1
|
| C | D | E | |||||||||||||
|     20 20
|
 | |||||||||||||
|  |
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2017-04-03 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |
 Следовательно, от одного комплекта мебели, перевозимого с вокзала В в магазин С, мы получим экономию в 1 рубль. Поэтому в клетку
Следовательно, от одного комплекта мебели, перевозимого с вокзала В в магазин С, мы получим экономию в 1 рубль. Поэтому в клетку