ОДНОСТОРОННИЕ ПРЕДЕЛЫ
Если  , но
, но  , то принято писать
, то принято писать 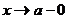 . Если
. Если  , но
, но  , то пишут
, то пишут  .
.
Пределы (если они существуют)
 , и
, и 
называют соответственно пределом слева функции  в точке а и пределом справа функции
в точке а и пределом справа функции  в точке а.
в точке а.
Равенство  является необходимым и достаточным условием для существования предела функции
является необходимым и достаточным условием для существования предела функции  в точке а. Пределы справа и слева называются односторонними.
в точке а. Пределы справа и слева называются односторонними.
Примеры: Найти односторонние пределы следующих функций:
1) 
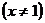 при
при  .
.
|  , ,  , отсюда видно, что если , отсюда видно, что если  , то , то 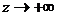 . .
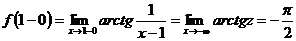 .
Пределы оказались неравными, следовательно, предела функции в точке .
Пределы оказались неравными, следовательно, предела функции в точке 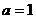 не существует. не существует.
|
2)  , (
, ( ) при
) при  .
.
 , т.к.
, т.к. 
 , т.к.
, т.к. 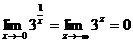 .
.
Пределы оказались неравными, следовательно, предела функции в точке  не существует.
не существует.
НЕПРЕРЫВНОСТЬ ФУНКЦИИ.
Определение. Функция  непрерывна в точке
непрерывна в точке  , если она определена в окрестности этой точки и существует предел
, если она определена в окрестности этой точки и существует предел 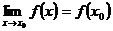
Определение детализируется в следующих условиях:
1) Функция должна быть определена в точке  , то есть должно существовать значение
, то есть должно существовать значение 
2) Должен существовать общий предел функции 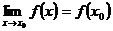 . Как отмечалось выше, это подразумевает существование и равенство односторонних пределов:
. Как отмечалось выше, это подразумевает существование и равенство односторонних пределов: 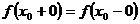 .
.
3) Предел функции в данной точке должен быть равен значению функции в этой точке: 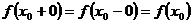
Отсюда следует, что 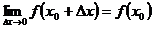 или
или 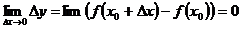 , т.е. если функция непрерывна в точке
, т.е. если функция непрерывна в точке  , то бесконечно малому приращению аргумента
, то бесконечно малому приращению аргумента  в этой точке соответствует бесконечно малое приращение функции
в этой точке соответствует бесконечно малое приращение функции 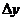 .
.

|
Справедливо и обратное утверждение: если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то функция непрерывна, т.к. в этом случае из соотношения (5) следует предел (4). Следовательно, для того, чтобы функция  была непрерывна в точке была непрерывна в точке  , необходимо и достаточно, чтобы ее приращение , необходимо и достаточно, чтобы ее приращение 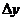 в этой точке стремилось к нулю вместе с приращением аргумента в этой точке стремилось к нулю вместе с приращением аргумента  . .
|
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области.
Функция, непрерывная в каждой точке своей области определения, непрерывна и во всей этой области.
Если две функции  и
и  непрерывны в точке
непрерывны в точке  , то в этой же точке непрерывны и функции
, то в этой же точке непрерывны и функции 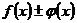 ;
;  ;
;  (если
(если  ).
).
ТОЧКИ РАЗРЫВАФУНКЦИИ И ИХ КЛАССИФИКАЦИЯ
Если условие непрерывности функции в точке  не выполнено, то функция имеет разрыв в этой точке.
не выполнено, то функция имеет разрыв в этой точке.
Говорят, что функция  имеет разрыв в точке
имеет разрыв в точке  первого рода, если существуют конечные пределы
первого рода, если существуют конечные пределы  и
и  , причем
, причем
1.Если  , то
, то  называется неустранимой точкой разрыва.
называется неустранимой точкой разрыва.
2.Если  ,
,  называется устранимой точкой разрыва, если
называется устранимой точкой разрыва, если  существует.
существует.
Функция  имеет в точке
имеет в точке  разрыв второго рода, если хотя бы одних из односторонних пределов функции в этой точке не существует, либо равен бесконечности.
разрыв второго рода, если хотя бы одних из односторонних пределов функции в этой точке не существует, либо равен бесконечности.
Если  , то разность
, то разность  называется скачком функции в точке
называется скачком функции в точке  (разрыв второго рода – неустранимый).
(разрыв второго рода – неустранимый).
 Пример: Для функции
Пример: Для функции 

 имеем
имеем
 , однако
, однако
 .
.
Следовательно, точка х = 2 является точкой устранимого разрыва функции  .
.
Примечание: Термин «устранимый разрыв» оправдан тем, что достаточно доопределить или переопределить (пополнить) функцию в точке. В рассмотренном примере нужно положить в  , тогда функция
, тогда функция


 является непрерывной в точке
является непрерывной в точке 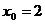 .
.
 Пример: Для функции
Пример: Для функции  точка х = 0 является точкой разрыва,
точка х = 0 является точкой разрыва,
т.к. в этой точке функция не определена ( не существует). При этом
не существует). При этом  ,
,  . Следовательно, точка
. Следовательно, точка  является точкой разрыва первого рода, а
является точкой разрыва первого рода, а  - скачок данной функции
- скачок данной функции
(т.е. если мы пополним эту функцию какой-то одной точкой, она все равно останется разрывной).
