Точный поиск подстроки в строке

 

В программах, предназначенных для редактирования текста, часто возникает задача поиска всех фрагментов текста, которые совпадают с заданным образ­цом. Обычно текст — это редактируемый документ, а образец — искомое слово, введенное пользователем. Эффективные алгоритмы решения этой задачи могут повышать способность текстовых редакторов к реагированию. Кроме того, алго­ритмы поиска подстрок используются, например, для поиска заданных образцов в молекулах ДНК[4].

Приведем формальную постановку задачи поиска подстрок (string-matching problem). Предполагается, что текст задан в виде массива Т [1.. π] длины n, а обра­зец — в виде массива Р [l..m] длины m ≤ n. Далее, предполагается, что элементы массивов Ри Т — символы из конечного алфавита Е. Например, алфавит может иметь вид Е = {0,1} или Е = {a, b,...,z}. Символы массивов Р и Тчасто называют строками (strings) или символами.

Говорят, что образец Р встречается в тексте Т со сдвигом s (occurs with shift s), если 0≤s≤n — m и T [s + l..s + m] = P[l..m] (другими словами, если при 1 ≤ j ≤ m T[s+j] = Р [j]). (Можно также сказать, что образец Р встречается в тексте Т, начиная с позиции s + 1.) Если образец Р встречается в тексте Тсо сдвигом s, то величину sназывают допустимым сдвигом (valid shift); в противном случае ее называют недопустимым сдвигом (invalid shift). За­дача поиска подстрок — это задача поиска всех допустимых сдвигов, с которыми заданный образец Р встречается в тексте Т. Эти определения проиллюстрирова­ны на рис. 40. В представленном на этом рисунке примере предлагается найти все вхождения образца Р = abaaв текст Т = abcabaabcabac. Образец встре­чается в тексте только один раз, со сдвигом s = 3. Говорят, что сдвиг s = 3 является допустимым. Каждый символ образца соединен вертикальной линией с соответствующим символом в тексте, и все совпадающие символы выделены серым фоном.

Рисунок.40. Задача поиска подстрок

 

Все данные алгоритмы, производят определенную предва­рительную обработку представленного образца, а затем находят все допустимые сдвиги; последняя фаза будет называться поиском. В табл. 2 приведены време­на предварительной обработки и сравнения для каждого из представленных в этой главе алгоритмов. Полное время работы каждого алгоритма равно сумме времени предварительной обработки и времени сравнения.

Таблица 2. Алгоритмы поиска подстрок и время их предварительной обработки и срав­нения

 

 

10.1 Простейший алгоритм поиска подстрок

 

В простейшем алгоритме поиск всех допустимых сдвигов производится с по­мощью цикла, в котором проверяется условие P[l..m] = Т [s + l..s + m] для каждого из n — mn + 1 возможных значений s[4].

 

Naive_String_Matcher(T, Р)

1 n <— length[T]

2 m <— length[P]

3 fors *— 0 ton — m

4 doifP[1.. m] = T[s + 1.. s + m]

5 then print “Образец обнаружен при сдвиге” s

 

Простейшую процедуру поиска подстрок можно интерпретировать графически как скольжение “шаблона” с образцом по тексту, в процессе которого отмечается, для каких сдвигов все символы шаблона равны соответствующим символам тек­ста. В частях а-г рис. 41, который иллюстрирует эту интерпретацию, показаны четыре последовательных положения, проверяемых в простейшем алгоритме по­иска подстрок. В каждой части рисунка вертикальные линии соединяют соответ­ствующие области, для которых обнаружено совпадение (эти области выделены серым цветом), а ломаные линии — первые, не совпавшие символы (если такие имеются). В части в показано одно обнаруженное вхождение образца со сдвигом s = 2. В цикле for, который начинается в строке 3, явным образом рассматрива­ются все возможные сдвиги. В строке 4 проверяется, действителен ли текущий сдвиг; в этот тест неявно включен цикл для проверки символов, которые находят­ся в соответствующих позициях, до тех пор, пока не совпадут все символы или не будет обнаружено несовпадение. В строке 5 выводится каждый допустимый сдвиг s.

Время работы процедуры NAIVE_STRING_MATCHER равно О((n — mn + 1) m), и эта оценка достаточно точна в наихудшем случае. Например, рассмотрим тек­стовую строку аⁿ (строку, состоящую из n символов о) и образец а™. Для каждого из n — mn +1 возможных значений сдвига s неявный цикл в строке 4 для проверки совпадения соответствующих символов должен произвести mn итераций, чтобы подтвердить допустимость сдвига. Таким образом, время работы в наихудшем случае равно 0((n — m + l)m), так что в случае mn = |n|2J оно становится рав­ным 0 (п²). Время работы процедуры Naive_String_Matcher равно времени сравнения, так как фаза предварительной обработки отсутствует.

Вскоре вы увидите, что процедура Naive_String_Matcher не является опти­мальной для этой задачи. В этой главе будет приведен алгоритм, время предвари­тельной обработки в котором в наихудшем случае равно 0 (mn), а время сравнения в наихудшем случае — 0 (n). Простейший алгоритм поиска подстрок оказывается неэффективным, поскольку информация о тексте, полученная для одного значе­ния s, полностью игнорируется при рассмотрении других значений s. Однако эта информация может стать очень полезной. Например, если образец имеет вид Р = = aaab, а значение одного из допустимых сдвигов равно нулю, то ни один из сдвигов, равных 1, 2 или 3, не могут быть допустимыми, поскольку Т[4] = b. В последующих разделах исследуется несколько способов эффективного исполь­зования информации такого рода.

Рисунок.41. Принцип работы простейшего алгоритма поиска подстрок для образца Р = aab и текста Т = acaabc

 

 

Алгоритм Рабина-Карпа

 

Рабин (Rabin) и Карп (Karp) предложили алгоритм поиска подстрок, показыва­ющий на практике хорошую производительность, а также допускающий обобще­ния на другие родственные задачи, такие как задача о сопоставлении двумерного образца. В алгоритме Рабина-Карпа время 0 (m) затрачивается на предваритель­ную обработку, а время его работы в наихудшем случае равно 0((n — m + 1)n). Однако с учетом определенных предположений удается показать, что среднее время работы этого алгоритма оказывается существенно лучше[4].

с ab.В этом алгоритме используются обозначения из элементарной теории чисел, такие как эквивалентность двух чисел по модулю третьего числа.

Для простоты предположим, что Е = {0,1,..., 9}, т.е. каждый символ — это десятичная цифра. (В общем случае можно предположить, что каждый символ — это цифра в системе счисления с основанием d, где d = |Е|.) После этого стро­ку из А; последовательных символов можно рассматривать как число длиной k. Таким образом, символьная строка 31415 соответствует числу 31415. При такой двойной интерпретации входных символов и как графических знаков, и как деся­тичных чисел, в этом разделе удобнее подразумевать под ними цифры, входящие в стандартный текстовый шрифт.

Для заданного образца Р [1..m] обозначим через рсоответствующее ему де­сятичное значение. Аналогично, для заданного текста Т[1.. π] обозначим через t_s десятичное значение подстроки Т [s + l..s + m] длиной m при s = 0,1,..., n — — m. Очевидно, что t_s= р тогда и только тогда, когда Т [s + l..s + m] = Р[1..m]; таким образом, s — допустимый сдвиг тогда и только тогда, когда t_s = р. Если бы значение р можно было вычислить за время 0 (m), а все значения t_s — за суммарное время 0 (n — m + 1), то значения всех допустимых сдвигов можно было бы определить за время 0 (m) + 0 (n — m + 1) = 0 (n) путем сравнения значения р с каждым из значений t_s. (Пока что мы не станем беспокоиться по поводу того, что величины ри t_sмогут оказаться очень большими числами.)

С помощью правила Горнера величину р можно вычислить за время 0 (m): р = Р [m] + 10 (Р [m - 1] + Ю (Р [m - 2] + • • • + 10 (Р [2] + 10Р[1]) •••)).

Значение можно вычислить из массива Т[1..m] за время 0(m) аналогич­ным способом. Чтобы вычислить остальные значения, t_n-m за время 0 (n - m), достаточно заметить, что величину t_s+i можно вычислить из величи­ны t_sза фиксированное время, так как

+1 = 10 ( — 10^m T [5+ I]) + T [5 + m + 1].

Например, если m = 5 и = 31415, то нужно удалить цифру в старшем разряде Т [5 + 1] = 3 и добавить новую цифру в младший разряд (предположим, это цифра Т [s + 5 + 1] = 2). В результате мы получаем + i = 10 (31415 — 10000 • 3) + 2 = = 14152.

Мы используем запись 0 (n — m + 1) вместо0 (n — m), поскольку всего имеется n — m + 1 различных значений, которые может принимать величина s. Слагаемое “+1” важно в асимптоти­ческом смысле, поскольку при m = n для вычисления единственного значения требуется время 0 (1), а не 0 (0).

Чтобы удалить из числа цифру старшего разряда, из него вычитается зна­чение 10^m-1T [s + 1]; путем умножения на 10 число сдвигается на одну позицию влево, а в результате добавления элемента Т [s + m, + 1] в его младшем разряде по­является нужная цифра. Таким обра­зом, число рможно вычислить за время 0 (mn), величины , ,..., — за время 0(n — m + 1), а все вхождения образца Р [l..m] в текст Т[1..п] можно найти, затратив на фазу предварительной обработки время 0 (mn), а на фазу срав­нения — время 0 (n — mn+ 1).

Единственная сложность, возникающая в этой процедуре, может быть связана с тем, что значения р и могут оказаться слишком большими и с ними бу­дет неудобно работать. Если образец Р содержит mn символов, то предположение о том, что каждая арифметическая операция с числом р (в которое входит mn цифр) занимает “фиксированное время”, не отвечает действительности. Эта проблема имеет простое решение вычислять значения р и по мо­дулю некоторого числа q. Поскольку вычисление величин р, и рекуррентного соотношения можно производить по модулю q, получается, что величина р по модулю q вычисляется за время 0 (mn), а вычисление всех величин 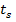по мо­дулю q — за время 0 (m — n + 1). В качестве модуля q обычно выбирается такое простое число, для которого длина величины 10d не превышает длины компьютер­ного слова. Это позволяет производить все необходимые вычисления с помощью арифметических операций с одинарной точностью. В общем случае, если имеет­ся d-символьный алфавит {0,1,..., d, — 1}, значение q выбирается таким образом, чтобы длина величины dq не превышала длины компьютерного слова, и чтобы с рекуррентным соотношением было удобно работать по модулю q. После этого рассматриваемое соотношение принимает вид t_s+1 — (d (t_s — Т [s + 1] h) + T [s + mn + 1]) mod q,

где h = d^m-1 (model) —значение, которое приобретает цифра “1”, помещенная в старший разряд m-цифрового текстового окна. Каждый символ здесь представлен десятичной цифрой, а вычисления производятся по модулю 13. В части а приведена строка текста. Подстрока длиной 5 символов выделена серым цветом. Находится числен­ное значение выделенной подстроки по модулю 13, в результате чего получается значение 7. В части б изображена та же текстовая строка, в которой для всех возможных 5-символьных подстрок вычислены соответствующие им значения по модулю 13. Если предположить, что образец имеет вид Р = 31415, то нужно найти подстроки, которым соответствуют значения 7 по модулю 13, поскольку 31415 = 7 (mod 13). Найдены две такие подстроки; они выделены серым цве­том. Первая подстрока, которая начинается в тексте на позиции 7, действительно совпадает с образцом, в то время как вторая, которая начинается на позиции 13, представляет собой т.н. ложное совпадение. В части в показано, как в течение фик­сированного времени вычислить значение, соответствующее данной подстроке, по значению предыдущей подстроки. Значение, соответствующее первой подстроке, равно 31415. Если отбросить цифру 3 в старшем разряде, произвести сдвиг числа влево (умножение на 10), а затем добавить к полученному результату цифру 2 в младшем разряде, то получим новое значение 14152. Однако все вычисления производятся по модулю 13, поэтому для первой подстроки получится значение 7, а для второй — значение 8. Итак, как видим, идея работы по модулю qне лишена недостатков, поскольку из =p (mod g) не следует, что t_a = р. С другой стороны, если ≠ р (mod g), то обязательно выполняется соотношение ≠ р и можно сделать вывод, что сдвиг s недопустимый. Таким образом, соотношение t_s= p (mod g) можно использовать в качестве быстрого эвристического теста, позволяющего исключить недопусти­мые сдвиги s. Все сдвиги, для которых справедливо соотношение t_s = p (mod g), необходимо подвергнуть дополнительному тестированию, чтобы проверить, что действительно ли сдвиг s является допустимым, или это просто ложное совпаде­ние (spurious hit). Такое тестирование можно осуществить путем явной проверки условия P [l..m] = Т[s + l..s + mn]. Если значение q достаточно большое, то мож­но надеяться, что ложные совпадения встречаются довольно редко и стоимость дополнительной проверки окажется низкой.

 

 

Рисунок.42. Алгоритм Рабина-Карпа

 

Сформулированная ниже процедура поясняет описанные выше идеи. В роли входных значений для нее выступает текст Т, образец Р, разряд d (в качестве значения которого обычно выбирается |ξ|) и простое число q.

RABIN_KARP_MATCHER(T, Р, d, q)

	n <— length[T]
	mn <— length[P]
	h *— dm-1 modq
	p <— 0
	to <— 0
	for i <— 1 m	> Предварительная обработка
	do p *— (dp + P[i])mod q	q
	<— (d + Т[t]) mod q
	for s <— 0 n — m	> Проверка
	do if p =
	then if P[1.. m]=	T[s +1.. s + m]
	then print “	Образец обнаружен при сдвиге” s
	if s < n — m
	then +i <- (d(ta	- T[s + l]/i) + T[s + m + 1]) mod i

 

пишем работу процедуры Rabin_Karp_Matcher. Все символы интерпрети­руются как цифры в системе счисления по основанию d. Индексы переменной t приведены для ясности; программа будет правильно работать и без них. В строке 3 переменной h присваивается начальное значение, равное цифре, расположенной в старшем разряде ш-цифрового текстового окна. В строках 4-8 вычисляется зна­чение р, равное Р [l..m] mod q, и значение to, равное Т [l..m] mod q. В цикле for в строках 9-14 производятся итерации по всем возможным сдвигам s. При этом сохраняется сформулированный ниже инвариант.

При каждом выполнении строки 10 справедливо соотношение:

=T[s + 1 .. s + m] mod q.

Если в строке 10 выполняется условие р = («совпадение»), то в строке 11 про­веряется справедливость равенства Р [l..m] = Т [s + l..s + m], чтобы исключить ложные совпадения. Все обнаруженные допустимые сдвиги выводятся в стро­ке 12. Если s < n - m (это неравенство проверяется в строке 13), то цикл for нужно будет выполнить хотя бы еще один раз, поэтому сначала выполняется строка 14, чтобы гарантировать соблюдение инварианта цикла, когда мы снова перейдем к строке 10. В строке 14 на основании значения mod q с использова­нием уравнения в течение фиксированного интервала времени вычисляется величина t_s+i mod q.

В процедуре Rabin_Karp_Matcher на предварительную обработку затра­чивается время 0 (m), а время сравнения в нем в наихудшем случае равно 0 ((n — m+ 1) m), поскольку в алгоритме Рабина-Карпа (как и в простейшем алгоритме поиска подстрок) явно проверяется допустимость каждого сдвига. Если Р = а^m и Т = аⁿ, то проверка займет время 0((n — m+l)m), поскольку все n — mn + 1 возможных сдвигов являются допустимыми.

Во многих приложениях ожидается небольшое количество допустимых сдви­гов (возможно, выражающееся некоторой константой с); в таких приложени­ях математическое ожидание времени работы алгоритма равно сумме величи­ны 0((n — m +1)m) = 0 (n+ mn) и времени, необходимого для обработки ложных совпадений. В основу эвристического анализа можно положить предпо­ложение, что приведение значений по модулю q действует как случайное отобра­жение множества £* на множество Z_q. Сделанное предположе­ние трудно формализовать и доказать, хотя один из многообещающих подходов заключается в предположении о случайном выборе числа q среди целых чисел подходящего размера. В таком случае можно ожидать, что число ложных совпадений равно О (n/q), потому что вероятность того, что произвольное число t_a будет эквивалентно р по модулю q, можно оценить как lg. Поскольку имеется всего 0(n) позиций, в которых проверка в строке 10 дает отрицательный результат, а на обработку каждого сов­падения затрачивается время О(mn), математическое ожидание времени сравнения в алгоритме Рабина-Карпа равно: 0(n) + 0 (т (v + n/q)), где v — количество допустимых сдвигов. Если v = 0 (1), a q выбрано так, что q*m, то приведенное выше время выполнения равно О(n). Другими слова­ми, если математическое ожидание количества допустимых сдвигов мало (О (1)), а выбранное простое число q превышает длину образца, то можно ожидать,

что для выполнения фазы сравнения процедуре Рабина-Карпа потребуется время О (n + m). Поскольку m * n, то математическое ожидание времени сравнения равно О(n).

Алгоритмы на графах

Свойства и типы графов

 

Многие вычислительные приложения естественным об­разом используют не только набор элементов (items), но также и набор соединений (connections) между парами таких элементов. Отношения, которые вытекают из этих соедине­ний, немедленно вызывают множество естественных вопро­сов. Существует ли путь от одного такого элемента к друго­му, вдоль этих соединений? В какие другие элементы можно перейти из заданного элемента? Какой путь от одного эле­мента к другому считается наилучшим?

Чтобы смоделировать подобную ситуацию, мы пользуем­ся объектами, которые называются графами (graphs)[5].

Теория графов, будучи крупной ветвью комбинаторной математики, интенсивно изучалась в течение не одной сот­ни лет. Было выявлено много важных и полезных свойств графов, однако многие задачи еще ждут своего решения.

Как и множество других предметных областей, которые приходилось изучать, алго­ритмическое исследование графов возникло сравнительно недавно. И хотя некоторые фундаментальные алгоритмы открыты давно, все же большая часть интереснейших алго­ритмов получена в течение нескольких последних десятилетий. Даже простейшие алгорит­мы на графах позволяют получить полезные компьютерные программы, а изучаемые нами нетривиальные алгоритмы относятся к числу наиболее элегантных и интересных из изве­стных алгоритмов.

Чтобы продемонстрировать все разнообразие приложений, использующих графы для обработки данных, начнем исследования алгоритмов в этой благодатной области с рассмот­рения нескольких примеров.

Географические карты. Путешественник, прежде чем отправиться в путь, желает по­лучить ответ на вопросы типа: ’’Какой маршрут из Принстона в Сан-Хосе потребует наи­меньших расходов?” Пассажир, для которого время дороже денег, хотел бы получить от­вет на такой вопрос: ’’Каким путем быстрее всего добраться из Принстона в Сан-Хосе?” Чтобы ответить на вопросы подобного рода, мы выполняем обработку информации, ха­рактеризующей соединения (пути следования) между элементами(городами и населенны­ми пунктами).

Гипертекст. Когда мы просматриваем Web-каталоги, мы сталкиваемся с документа­ми, содержащими различные ссылки (соединения) на другие документы, и переходим от документа к документу, щелкая мышью на этих ссылках. Сама по себе ’’всемирная пау­тина" представляет собой граф, в котором в качестве элементов выступают документы, а соединения суть связи. Алгоритмы обработки графов являются важными компонентами поисковых механизмов, которые помогают определить местоположение информации в Web.

Микросхемы. Микросхемы содержат такие элементы, как транзисторы, резисторы, конденсаторы, которые связаны между собой сложнейшим образом. Для управления ма­шинами, изготавливающими микросхемы, и для проверки, выполняют ли эти цепи задан­ные функции, используются компьютеры. Мы хотим получить ответы на простые вопросы наподобие "Имеются ли в цепи условия для короткого замыкания?" и на более сложные вопросы, такие как "Можно ли скомпоновать микросхему на кристалле таким образом, чтобы шины не пересекались?". В данном случае, ответ на первый вопрос зависит толь­ко от свойств соединений (шин), в то время как для ответа на второй вопрос потребует­ся подробная информация о шинах, элементах, которые эти шины соединяют, и физи­ческих ограничениях, накладываемых кристаллом.

Составление расписаний. Производственный процесс требует решения различных за­дач под воздействием некоторого множества ограничений, по условиям которых реше­ние одной задачи не может быть начато до тех пор, пока не будет завершено решение другой задачи. Мы представляем эти ограничения в виде соединений между этими зада­чами (элементами), при этом перед нами возникает задача составления расписаний (scheduling) в ее классическом виде: как построить временной график решения задач та­ким образом, чтобы удовлетворить заданным ограничениям и завершить данный процесс за минимально возможное время?

Транзакции. Телефонная компания поддерживает базу данных телефонного трафика. В этом случае соединения представляют телефонные вызовы. Мы заинтересованы в том, чтобы знать все, что касается характера структуры соединений, ибо хотим проложить провода и установить коммутаторы так, чтобы эффективно справляться с телефонным трафиком. Еще одним примером может служить то, как финансовое учреждение отсле­живает операции купли/продажи на рынке. Соединение в рассматриваемом случае пред­ставляет собой передачу денег продавцом покупателю. Знание свойств структуры соеди­нений в данном случае помогает лучше понять особенности рынка.

Сети. Сеть вычислительных машин состоит из взаимосвязанных узлов, которые посы­лают, передают дальше и получают сообщения различных видов. Мы заинтересованы не только в обеспечении возможности получать сообщения из любого другого узла, но и в том, чтобы эта возможность сохранялась для всех пар узлов и в случае изменения кон­фигурации сети. Например, возможно, потребуется проверить работу конкретной сети, чтобы убедиться в отсутствии некоторого небольшого подмножества узлов или соедине­ний, настолько критичного для работы всей сети, что его утрата может привести к разъе­динению остальных пар узлов.

Структура программы. Компилятор строит графы для представления структуры вызо­вов крупной системы программного обеспечения. Элементами в этом случае являются различные функции или программные модули, составляющие систему; соединения отож­дествляются либо с возможностью того, что одна функция может вызвать другую функ­цию (статический анализ), или с фактическим вызовом, когда система находится в рабо­чем состоянии (динамический анализ). Нам нужно выполнить анализ графа, чтобы определить, как достичь максимальной эффективности при выделении системных ресур­сов для конкретной программы.

Эти примеры демонстрируют, насколько широк диапазон приложений, для которых граф служит подходящей абстракцией, и, соответственно, диапазон вычислительных за­дач, с которыми доведется столкнуться при работе с графами. Эти задачи являются глав­ной темой настоящей книги. Во многих подобного рода приложениях, с которыми при­ходится иметь дело на практике, объем обрабатываемых данных поистине огромен, так что именно эффективность алгоритма решает, будет ли вообще работать соответствующее приложение.

Первые алго­ритмы, которые мы изучали самым подробным образом, т.е. алгоритмы объединения-по­иска представляют собой простейшие алгоритмы на графах. Любая связная структура данных может быть представлена в виде графа, а некоторые известные алго­ритмы обработки деревьев и других связных структур представляют собой частные слу­чаи алгоритмов на графах. Назначение данной главы заключается в том, чтобы обеспечить контекст для изучения широкого набора алгоритмов на графах, от простейших до очень сложных.

Задача изучения рабочих характеристик алгоритмов на графах представляет собой достаточно сложную проблему, что можно объяснить следующими причинами:

■ Стоимость алгоритма зависит не только от свойств множества элементов, но так­же и от многочисленных свойств соединений (и глобальных свойств графа, обус­ловленных свойствами соединений).

■ Трудность разработки точных моделей типов графов, с которыми, возможно, при­дется столкнуться.

Часто исходят из предположения, что используемым алгоритмам на графах при­дется работать в условиях, наиболее неблагоприятных для их рабочих характеристик, даже если во многих случаях на практике такие предположения представляют собой пессими­стическую оценку. Многие из этих алгоритмов опти­мальны и не требуют больших непроизводительных затрат. В отличие от них, существуют алгоритмы, которые затрачивают одинаковые ресурсы на обработку всех графов задан­ного размера. С достаточной степенью точности можно предсказать, как поведут себя такие алгоритмы в конкретных условиях. В тех случаях, когда такие предсказания невоз­можны, нам придется уделить особое внимание свойствам графов различных типов, ко­торые, в соответствии с нашими ожиданиями, проявятся в конкретных практических си­туациях, и оценить, как эти свойства могут повлиять на производительность выбранных алгоритмов.

 

 

Глоссарий

 

С графами связана обширная терминология. Большинство употребляемых терминов имеют прямое определение, и для удобства ссылок целесообразно рассматривать их в ка­ком-то одном месте, а именно, в данном разделе[5].

 

Определение 8: Граф есть некоторое множество вершин и некоторое множество ребер, соединяющих пары различных вершин (одно ребро может соединять максимум одну пару вершин).

 

Мы используем цифры от 0 до V-1 в качестве имен вершин графа, состоящего из V вершин. Основная причина выбора именно этой системы обозначений заключается в том, что мы получаем быстрый доступ к информации, соответствующей каждой вершине, пу­тем индексирования векторов.

В качестве стандартного определения графа будет принято определение 8, но при этом стоит заметить, что в нем исполь­зованы два технических упрощения. Во-первых, оно не позволяет дублировать ребра (ма­тематики иногда называют такие ребра параллельными (parallel), а граф, который может содержать такие ребра, мультиграфом (multigraph)). Во-вторых, оно не допускает ребер, замыкающихся на одну и ту же вершину; такое ребро называются петлей (self-loop). Гра­фы, в которых нет параллельных ребер или петлей, иногда называют простыми графами (simple graph).

Употребляем понятия простых графов в формальных определениях, поскольку таким путем легче выразить их основные свойства, а также ввиду того, что параллельные ребра и петли во многих приложениях не нужны. Например, можно ограничить чис­ло ребер простого графа заданным числом вершин.

 

Свойство графа. Граф, состоящий из V вершин, содержит не более V(V — 1)/2ребер.

 

Эти ограничения не имеют места в условиях существования параллельных ребер: граф, не принадлежащий к категории простейших, может содержать всего лишь две вершины и миллиарды ребер, соединяющие их (или даже одну вершину и миллиарды петель).

В некоторых приложениях удаление параллельных ребер и петель можно рассматри­вать как задачу обработки данных, которую должны решать сами приложения. В других приложениях, возможно, вообще не имеет смысла проверять, представляет ли заданный набор ребер простой граф. На протяжении данной книги, там, где удобно проводить ана­лиз конкретного приложения или разрабатывать алгоритм с применением расширенно­го определения графа, использующего понятия параллельных ребер или петель. В общем случае из контекста ясно, в каком смысле используется термин "граф": "простой граф", "мультиграф" или "мульти­граф с петлями".

Математики употребляют термины вершина(vertex) и узел (node) попеременно, но мы будем главным образом пользоваться термином вершинапри обсуждении графов и терми­ном узел при обсуждении представлений графов, например, структур данных в C++. Обычно мы полагаем, что у вершины есть имя и что она может нести другую связанную с ней информацию. Аналогично, слова дуга (arc), ребро (edge)исвязь (link) также широко используются математиками для описания абстракций, предусматривающих соединение двух вершин, однако мы последовательно будем употреблять термин ребропри обсужде­нии графов и термин связь при обсуждении структур данных в C++.

Если имеется ребро, соединяющее две вершины, будем говорить, что обе эти верши­ны смежные (adjacent) по отношению друг к другу, а ребро инцидентно (incident on) этим вершинам. Степень (degree) вершины есть число ребер, инцидентных этой вершине. Мы употребляем обозначение v-w для обозначения ребра, соединяющего вершины y и w; обо­значение w-v представляет собой еще одно возможное обозначение того же ребра.

Подграф (subgraph) представляет собой подмножество ребер некоторого графа (и свя­занных за ними вершин), которые сами образуют граф. По условиям многих вычисли­тельных задач требуется определить на некотором графе подграфы различных типов. Если выделить некоторое подмножество вершин графа и все ребра графа, соединяющие пары вершин этого подмножества, то такое подмножество называется индуцированным подгра­фом (induced subgraph), ассоциированным с этими вершинами.

Мы можем начертить граф, обозная точками его вершины и соединяя эти точки ли­ниями, которые будут служить ребрами. Чертеж дает нам некоторое представление о структуре графа; но это представление может оказаться обманчивым, ибо определение графа дается вне зависимости от его представления. Например, два чертежа и список ре­бер, представляют один и тот же граф, поскольку этот граф - всего лишь (неупорядоченное) множество его вершин и (неупорядоченное) мно­жество его ребер (пар вершин), и ничего более. Достаточно рассматривать граф просто как некоторое множество ребер, однако мы будем изучать и другие представления* ко­торые лучше других подходят для использования в качестве базы для структур данных типа граф. Перенесение вершин заданного графа на плоскость и вычерчивание этих вершин и соединяющих их ребер по­зволяет получить чертеж графа(graph drawing). Возможно множество вариантов размещения вершин, стилей изоб­ражения ребер, поскольку эстетические требования, предъявляемые к изображению, практически бесконечны. Алгоритмы построения чертежей, соблюдающие различ­ные естественные ограничения, подверглись интенсивно­му изучению, в результате которых были получены мно­гие удачные приложения. Например, одно из простейших ограничений есть требование, со­гласно которому ребра не должны пересекаться. Планар­ный граф (planar graph) принадлежит к числу тех, которые можно построить без пересечения ребер. Возможность построения чертежа графа представляет собой благодатное поле для исследо­ваний, в то же время на практике построить хороший чертеж графа не так-то просто. Многие графы с очень большим числом вершин и ребер, являются абстрактны­ми объектами, чертеж которых неосуществим.

В некоторых приложениях, например, выполняющих анализ географических карт или электрических схем, для построения чертежа графа требуется обширная информа­ционная база, поскольку их вершины соответствуют точ­кам на плоскости, а расстояния между ними должны быть выдержаны в определенном масштабе. Та­кие графы называют эвклидовыми (Euclidean graph). Если целиком сосредоточиться на исследовании свойств соединений, то мы, возможно, предпочтем рассматривать метки вершин как предназначенные только для удобства обо­значения, а два графа считать одинаковыми, если они отличаются друг от друга только метками вершин. Два графа называются изоморфными (isomorphic), если можно поменять метки вершин на одном из них таким образом, чтобы набор ребер этого графа стал иден­тичным набору ребер другого графа.

Определение 9: Путь (path) в графе есть последова­тельность вершин, в которой каждая следующая вершина (после первой), является смежной с предыдущей вершиной на этом пути. Все вершины и ребра, составляющие про­стой путь, различны. Циклом (cycle) называется простой путь, у которого первая и последняя вершина одна и та же.

 

Иногда используют термин циклический путь(< cyclic path) для обозначения пути, у которого первая и последняя вершина одна и та же (и который в других отношениях не обязательно является простым); также употребляют тер­мин контур (tour) для обозначения циклического пути, ко­торый включает каждую вершину. Эквивалентное опреде­ление рассматривает путь как последовательность ребер, которая соединяет соседние вершины. Мы отражаем это обстоятельство в используемых нами обозначениях, соеди­няя имена вершин в путь точно так, как мы соединяем их в представлении ребра. Например, простой путь, содержит последовательности 3-4-6-0-2 и 9-11-12, а циклами графа являются последовательности 0-6-4-3-5-0 и 5-4-3-5. По определению длина(length) пути или цикла представляет собой количество образующих их ребер.

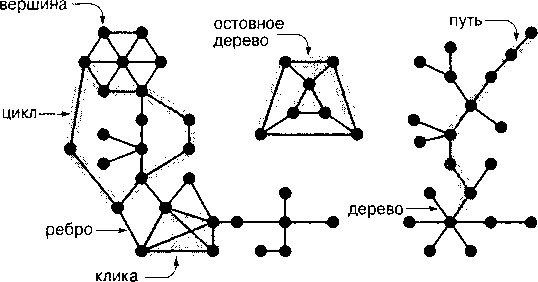Рисунок.43. Терминология, употребляемая в теории графов

Термин максимальный связный подграф (maximal connected subgraph) означает, что не су­ществует пути из вершины такого подграфа в любую другую вершину графа, который не содержался бы в подграфе. Интуитивно, если бы вершины были физическими объекта­ми, такими как, скажем, узлы или бусинки, а ребра были бы физическими соединения­ми, такими как, например, нити или провода, то в случае связного графа, находясь в ка­кой-либо его вершине, можно было бы смотать нить в один клубок, в то время как несвязный граф распался бы на два или большее число таких клубков.

 

Определение 10: Ациклический связный граф называется деревом (tree). Множество деревьев называется лесом (forest). Остовное дерево (spanning tree) связно­го графа есть подграф, который содержит все вершины этого графа и представляет со­бой единое дерево. Остовный лес (spanning forest) графа есть подграф, который содержит все вершины этого графа и при этом является лесом.

Например, граф имеет три связных компоненты и охватывается лесом 7-8 9-10 9-11 9-12 0-1 0-2 0-5 5-3 5-4 4-6 (существует множество дру­гих остовных лесов). На рис. 43 эти и некоторые другие свойства отображены на большем из графов.

На­пример, граф GсV вершинами есть дерево тогда и только тогда, когда он удовлетворяет одному из четырех условий:

 

■ Gсодержит V- 1 ребро и ни одного цикла.

■ Gсодержит V- 1 ребро и представляет собой связный граф.

■ Каждую пару вершин в G соединяет в точности один простой путь.

■ G представляет собой связный граф, в то же время при удалении любого из ребер он перестает быть связным.

 

Любое из указанных выше условий необходимо и доста­точно для доказательства остальных трех, и на их основе можно вывести другие свойства деревьев. Формально, мы должны выбрать одно из указанных ус­ловий в качестве определения; фактически, они