К численному дифференцированию чаще всего обращаются, когда значения функции известны в отдельных точках (например, результаты экспериментов в виде таблиц).
Приближенное значение производной функции Дх) в точке х0 при выбранном шаге к > 0 находится по одной из формул:
Общие вопросы численного дифференцирования можно рассмотреть на примере заданной на отрезке [а, Ь] функции Дх), имеющей непрерывные производные до (л+1) порядка, представленной в виде суммы
Дх) = Рп(х)+К(х), где Рп(х) — интерполяционный полином степени п, построенный по узлам интерполяции х0, хи..., х„; Р(х) — остаточный член.
Обычно в формуле (3.11) берут в той или иной форме интерполяционный многочлен и в соответствии с (3.12) находят приближенные значения произ водных в узлах интерполяции.
Интерполируя многочленом Ньютона и сравнивая его с разложением функции в ряд Тейлора, находят так называемые разностные формулы численного дифференцирования
К численному интегрированию обращаются в тех случаях, когда функция определена на всем промежутке интегрирования, но интеграл от нее не выражается в элементарных функциях.
ь Определенный интеграл \/(х)с1х выражает площадь криволинейной трапеции аАВЬ (рис. 3.4). Эту площадь можно вычислить приближенно, если заменим кривую у т Дх) некоторой ломаной линией. Разбив интеграл [а, Ь] на п
равных частей п — ------ и определив в точках деления х0, хь..., х„ ординаты
п у0, Уь •••, Уп, площадь интеграла приближенно можно определить по формуле
трапеций
[/(*)<&- —— (у0+2у1+2у2 +... + 2уп_1 + уп).
Другой простейшей формулой численного интегрирования является формула парабол (или формула Симпсона), основанная на замене подынтегральной кривой суммой дуг парабол второго порядка.
Разработаны и другие способы приближенного вычисления интегралов. Выше, при рассмотрении метода имитационного моделирования, отмечалось, что эффективным способом решения интегралов может служить метод Монте-Карло. Применяются также графические методы дифференцирования и интегрирования, отличающиеся самой невысокой точностью, но обладающие простотой и наглядностью.
Аналитические методы решения дифференциальных уравнений, являющихся неотъемлемой частью многих математических моделей, получили широкое развитие.
Наиболее часто встречаются дифференциальные уравнения, решить которые в замкнутой форме не удается. В этом случае приходится применять приближенные методы решения уравнений. Во многих случаях может оказаться полезным представление решения в виде ряда Тейлора.
Метод Пикара применим к решению нормальных систем дифференциальных уравнений и, следовательно, дифференциальных уравнений высшего по рядка.
Достаточно часто при решении уравнений вида у' = =Цх, у) применяем
метод Рун ге-Кутта.
21 методы планирования экспериментов в приложении к горному производству
Если информации о рассматриваемом процессе недостаточно или изучае-I мое явление настолько сложно, что не представляется возможным составить | детерминированную модель, то используют экспериментально-статистические
методы. Различают пассивный и активный эксперименты. •
Пассивный эксперимент — традиционный метод, когда с целью изучения
процесса ставится большая серия опытов с поочередным варьированием каждой из переменных. К пассивному эксперименту относится сбор статистических данных работы установок, предприятий с последующей обработкой ме тодами математической статистики. Традиционное планирование эксперимента по Зейделю-Гауссу состоит в том, что факторам (д;,, х2,..., хк),
определяющим в конечном счете значение отклика (выхода) у, задают ряд I значений (уровней). На каждом уровне одного фактора ставятся опыты по | всем уровням другого. При равном числе т уровней, параллельных измерений | на каждом уровне п и факторов к необходимо выполнить количество опытов Ы= птк.
22. Оптимальный двухуровневый план
Задачей активного планирования экспериментов служит кратчайший путь нахождения функции отклика

связывающей параметр оптимизации (отклик, выход) у с переменными про
цесса х\, х2,..., хк? называемыми факторами. Координатное пространство5jcb х2,
...,хк — это факторное пространство, а графическое изображение функции от
клика в пространстве — поверхность отклика (на плоскости это совокупность
линий равных уровней функции отклика). ' :
При планировании экспериментов факторы имеют фиксированные значения уровней. Если эксперименты проводятся лишь при двух значениях факторов и при этом в экспериментах осуществляются все возможные комбинации факторов, то постановка опытов по такому плану носит название полного факторного эксперимента (ПФЭ или 2* плана).
Постановка полного факторного эксперимента сводится к выбору уравнения регрессии, составлению плана опытов, расчету коэффициентов регрессии, оценке значимости этих коэффициентов, анализу уравнения регрессии.
Выбор уравнения регрессии зависит от числа изучаемых факторов и априорной информации о характере их влияния на функцию отклика и наличия эффекта взаимодействия. Для двух факторов уравнение регрессии без членов высшего порядка будет

и для трех факторов —

В этих уравнениях хь х2, хъ — значения факторов; Ь0 — свободный член при Х\ = 0; Ъ\, Ь2, Ь3 — коэффициенты регрессии при соответствующих хь характеризующие влияние данного фактора на функцию отклика у; bi2, bn, Ь2Ъ —-'коэффициенты регрессии, свидетельствующие о двойном взаимодействии факторов; Ь\гг — то же, свидетельствует о тройном взаимном влиянии факторов. Аналогично записываются уравнения для четырех и более факторов.
Пример 61.
Построить план первого порядка экспериментов р/р0 = ftp, w) для созда ния математической модели в виде полинома:
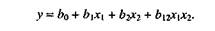
Центр исследуемой области/? = 80 МПа, w = 16% и в него переносится начало координат. Выбираем интервал варьирования переменных р, w: Ар = ± 20 Мпа, Aw = + 2%. Этот этап решается на основе знания объектов исследования (прессования торфа) и основных закономерностей влияния р, w на степень прессования р/ро (р — плотность брикетов, р0 — насыпная плотность торфа). На следующем этапе переходим кодированным переменным дгь х2:

Составим матрицу планирования экспериментов по определению зависимости у = Дхь х2), где для простоты обозначили у = — (табл. 4.3).
Ро

|
| Матрица планирования экспериментов по определению зависимости / |
| Фактор | Уровень | Шаг варьирования | ||
| -1 | + 1 | |||
| Р w | 80 16 |

|