Основная теорема теории игр (Джон фон Нейман)

Для произвольной платежной матрицы антагонистической игры нижний выигрыш первого игрока равен верхнему проигрышу второго:

и существует по крайней мере одна пара смешанных стратегий игроков (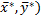, которая реализует данный выигрыш V первого игрока (проигрыш V второго игрока):

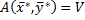
Общее значение V величин и называют ценой игры, а любая реализующая его пара стратегий (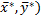 игроков называется парой их оптимальных стратегий игры.

Пара оптимальных стратегий игры (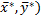 и цена игры V образуют решение игры.

Легко показать, что пара оптимальных смешанных стратегий (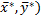 игроков образует ситуацию равновесия в игре.

Т.О., любая дискретная позиционная антагонистическая игра имеет ситуацию равновесия и тем самым решение в смешанных стратегиях игроков. Игроки снова могут без ущерба для своих результатов сообщить противнику свои оптимальные смешанные стратегии, т.к. противник не сможет использовать эту информацию для улучшения своего поведения в игре.

Теорема об активных стратегиях

В общем случае некоторые из чисел , могут быть равными нулю, т.е. не все стратегии, доступные игроку, входят в его оптимальную смешанную стратегию.

Стратегии, которые входят в оптимальную смешанную стратегию с отличными от нуля вероятностями, называются активными.

ТЕОРЕМА (об активных стратегиях). Если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры V, независимо от того, что делает другой игрок, если только тот не выходит за пределы своих активных стратегий (т.е. пользуется любой из них в чистом виде или смешивает в любых пропорциях).

Заметим, что теорема не означает, что второй игрок может играть произвольно, т.к. первый игрок заметит, что его противник играет не по оптимальной смешанной стратегии, также отступит от своей оптимальной смешанной стратегии (подстроится под противника) и сможет сделать свой выигрыш больше V.

Методы решения антагонистических игр.

Частные случаи.

1) в платежной матрице A существует седловой элемент

тогда существует решение в чистых стратегиях: V= ,

2) использование факта доминирования строк и столбцов в платежной матрице A, если таковое имеется

Говорят, что i-ая строка платежной матрицы A доминирует ее k-ую строку, если выполняется неравенство:

И, кроме того,

Очевидно, что в данном случае чистая стратегия 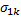является бесполезной для первого игрока и всегда хуже стратегии , поэтому k-ая строка оказывается лишней и ее можно исключить из матрицы A без ущерба для решения игры. Матрица A при этом упрощается вследствие уменьшения ее размерности.

Аналогично по столбцам:

j-ый столбец матрицы A доминирует ее l-ый столбец, если

и кроме того , тогда чистая стратегия всегда лучше и стратегию можно исключить.

Теорема. Если строка с номером i₁ платежной матрицы A игры доминирует с какой-либо другой строкой, то:

а) в игре существует оптимальная стратегия

б) всякая оптим. стратегия первого игрока в игре с матрице 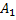, отличающейся от A исключением строки с номером i₁, является в то же время и оптимальной стратегией первого игрока в игре с матрицей A после добавления нуля в состав компонент вероятностного распределения:

Аналогичное утверждение справедливо для игр,у кот. матрица А содержит доминируемые столбцы.

Пример: рассмотрим игру

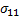
второй столбец доминирует четвёртый

третья строка доминирует первую

второй столбец доминирует третий

первая строка доминирует вторую

первый столбец доминирует второй

Т.О. игра имеет седловой элемент, цену игры V=1 и пару оптим. стратегий (, т.е.

3) решение игр с платежной матрицей 2х2

Пусть в платежной матрице 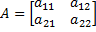игры 2х2 нет седлового элемента

Оптимальные стратегии 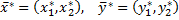удовлетворяет соотношению

Т.к. - оптимальная стратегия второго игрока, то по свойству равновесных стратегий, имеем:

Т.к. , то равенство возможно только при:

(подтверждается теорема об активных стратегиях)

Аналогично имеем:

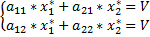
Если Δ= , то система имеет единственное решение.

Если нет седлового элемента, то это условие выполняется, т.к. иначе строки были бы пропорциональны, что означало бы наличие у матрицы А доминирования одной строки (столбца) над другой.

Добавляя равенства и решая системы, находим:

Пример: решить игру

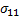
Δ=

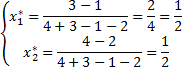
Решение игры:

V=2.5;