Игра, в которой игрок выбирает стратегии из бесконечного множества стратегий, называется непрерывной или бесконечной игрой.
Простейшей математической моделью таких подобных игр являются игры на квадрате
Альтернативами первого игрока здесь являются значения координаты X(
т. А, принадлежащей квадрату на плоскости (x,y) с координатами вершин (0,0), (0,1),(1,1),(1,0)
Альтернативами второго игрока являются значения координаты y (
той же т. А. Предполагается, что в каждой точке А этого квадрата определена платежная функция A(x,y), обычно называемая ядром, имеющая смысл выигрыша первого игрока:
При этом выигрыш второго игрока определяется из условия:
т.е.
Очевидно, непрерывная игра, заданная на любом прямоугольнике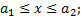 
легко сводится к непрерывной игре на квадрате, подходящей заменой аргументов x,y
Реализация принципа гарантированного результата в классах чистых стратегий игроков дает значение нижнего выигрыша первого игрока 
и верхнего проигрыша второго игрока 
Причем для любой непрерывной A(x,y): 
Если 
= 
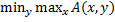
то игра имеет седловую точку 
, являющуюся ситуацией равновесия в игре.
Для произвольной непрерывной платежной функции A(x,y) существования седловой точки в квадрате (
гарантировать нельзя.
Рассмотрим некоторые из частных свойств A(x,y), гарантирующие существование у нее седловой точки в области определения:
1) если функция A(x,y) – непрерывна и может быть представлена в виде суммы двух функций, зависящих только от аргумента X и только от аргумента Y:
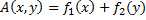
то A(x,y) имеет в области определения седловую точку.
2) если функция A(x,y) – непрерывна в квадрате и представима в виде:
то A(x,y) имеет в области определения седловую точку.
3) если платежная функция A(x,y) дифференцируема и для любого значения 
выпукла вверх по Х и одновременно для любого значения 
выпукла вниз по y, то она имеет на квадрате (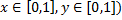 
седловую точку.
Достаточным условием для выпуклости вверх A(x,y) по x при любом y является неравенство:
а достаточным условием для выпуклости вниз A(x,y) по y при любом x является неравенство:
«Правило рюмки»
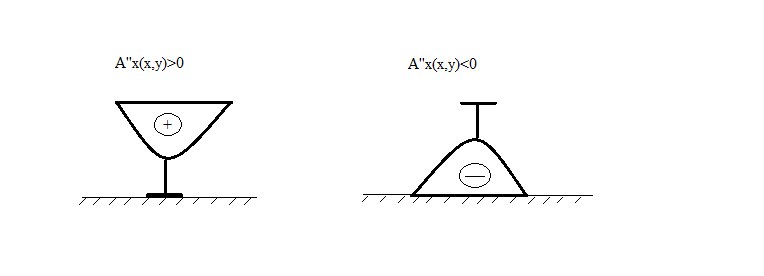
ТО при выполнении этих неравенств в непрерывной игре существует ситуация равновесия в чистых стратегиях.
Пример
Решить игру на квадрате 
, с платежной функцией:
Следовательно, игра имеет седловую точку и решение в чистых стратегиях.
Обозначим,
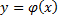- линия минимумов – значение переменной y,которое реализует 
а через 
– линия максимумов, значение переменной x, которое реализует
Координаты седловой точки удовлетворяют двум уравнениям:
т.е. являются решением системы уравнений:
Найдем 
на линии минимумов выполняется соотношение
т.е. 
Найдем x =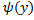 
– линию максимумов.
На линии максимумов выполняется равенство:
или
Обобщая, получаем функции:
линии минимумов
линия максимумов
Координаты - точка пересечения графиков 
и x= 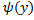является решением системы уравнений:
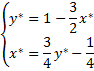
определяющей седловую точку платежной функции A(x,y)
Решая систему находим:
Цена игры V= 
Обсудим понятие смешанных стратегий в непрерывных играх.
Смешанная стратегия в бесконечной игре есть случайный процесс выбора числа X из промежутка [0,1].
Вероятностное распределение СВ X и Y можно характеризовать интегральными законами распределения – функциями распределения
Пара интегральных законов распределения (F(x), G(y)) называется ситуацией игры в классе смешанных стратегий игроков в непрерывной игре на квадрате
Рассмотрим случай, когда функции F(x) и G(y) – непрерывны и дифференцируемы, а соответствующие плотности распределения F’(X)=f(x) и G’(Y)=g(y)
тогда математическое ожидание выигрыша первого игрока для любого заданного будет равно:
И, следовательно, поскольку у выбрано по функции распределения G(y), то общее ожидание выигрыша первого игрока будет равно:
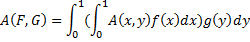
Т.к. игра с нулевой сумой, т.о. математическое ожидание выигрыша второго игрока - A(F, G)
Нижним выигрышем 
первого игрока и верхним проигрышем 
второго игрока назыв. величины:
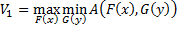
если они существуют
Можно доказать, что 
Основная теорема непрерывных игр, аналогичная теореме Неймана, утверждает, что в случае непрерывной платежной функции A(x,y) в квадрате (
имеет место равенство:
т.е.
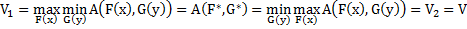
и имеется по крайней мере одна пара оптимальных смешанных стратегий игроков 
, которая реализует данный выигрыш первого игрока (проигрыш второго игрока)
Общее значение V величин 
называют ценой игры.
Можно показать, что 
т.е. параоптимальных стратегий образует ситуацию равновесия в игре, заданной функцией A(x,y).
Пара и значение V называется решением игры.