Формулы по теории вероятности
I. Случайные события
Основные формулы комбинаторики
а) перестановки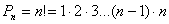 
.
б) размещения 
в) сочетания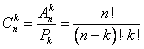 
.
Классическое определение вероятности.
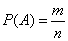, где 
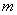- число благоприятствующих событию 
исходов,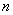 
- число всех элементарных равновозможных исходов.
Вероятность суммы событий
Теорема сложения вероятностей несовместных событий:
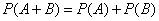
Теорема сложения вероятностей совместных событий:
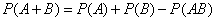
Вероятность произведения событий
Теорема умножения вероятностей независимых событий:
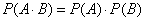
Теорема умножения вероятностей зависимых событий:
,
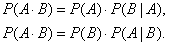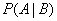- условная вероятность события при условии, что произошло событие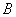 
,
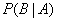- условная вероятность события 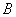при условии, что произошло событие .
Формула полной вероятности
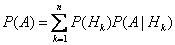, где 
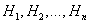- полная группа гипотез, то есть 
, 
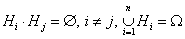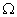- достоверное событие.
Формула Байеса (формула Бейеса). Вычисление апостериорных вероятностей гипотез
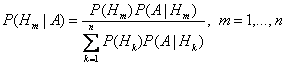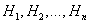, где - полная группа гипотез.
Формула Бернулли
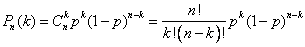- вероятность появления события ровно 
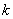раз при 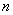независимых испытаниях, 
- вероятность появления события при одном испытании.
Наивероятнейшее число наступления события.
Наивероятнейшее число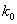 
появления события при 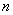независимых испытаниях:
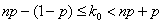, - вероятность появления события при одном испытании.
Локальная формула Лапласа
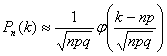- вероятность появления события ровно 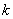раз при 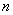независимых испытаниях, - вероятность появления события при одном испытании,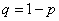 
.
Интегральная формула Лапласа
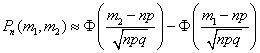- вероятность появления события не менее 
и не более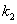 
раз при 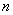независимых испытаниях, - вероятность появления события при одном испытании, .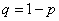
11. Оценка отклонения относительной частоты от постоянной вероятности :
.
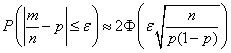II. Случайные величины
Ряд распределения дискретной случайной величины
| 
| 
| ……. | 
|
| 
| 
| ……. | 
|
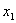
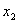
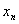
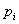
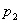
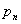
Сумма вероятностей всегда равна 1. 
Функция распределения (интегральная функция распределения)
Функция распределения случайной величины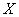 
определяется по формуле 
. Это неубывающая функция, принимающая значения от 0 до 1. Если задана плотность распределения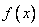 
, то функция распределения выражается как 
.
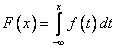Функция распределения (интегральная функция распределения)
Плотность распределения случайной величины 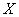определяется по формуле 
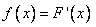. Существует только для непрерывной случайной величины. Для нее выполняется условие нормировки: 
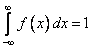(площадь под кривой равна 1).
Вероятность попадания случайной величины в заданный интервал
Может быть вычислена двумя способами:
1) через функцию распределения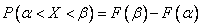 
2) через плотность распределения 
Математическое ожидание случайной величины
1) Для дискретной случайной величины 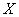, заданной рядом распределения:
1) Для непрерывной случайной величины 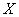, заданной плотностью распределения:
.
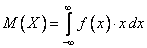Дисперсия случайной величины
По определению дисперсия – это второй центральный момент: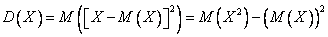 
.
1) Для дискретной случайной величины 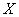, заданной рядом распределения:
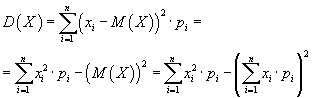
1) Для непрерывной случайной величины 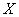, заданной плотностью распределения:
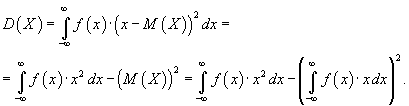
Среднее квадратическое отклонение случайной величины
Начальный момент r–го порядка случайной величины
.
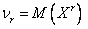В частности, первый начальный момент – это математическое ожидание: 