ЛЕКЦИЯ 1.2. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Понятие системы линейных уравнений, основные определения
Если заданы m линейных уравнений с n неизвестными и требуется найти n чисел, которые одновременно удовлетворяют каждому из m уравнений, то мы имеем систему линейных уравнений. Такие системы могут решаться методами линейной алгебры.
Определение. mхn системой линейных уравнений называется система вида:
(1)
где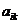 
– числа – коэффициенты системы; 
– числа – свободные члены системы;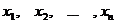 
– неизвестные или переменные (
).
Сокращенная запись системы (1):
, 
(2)
Определение Если все свободные члены системы равны нулю
( = 0), то система (1) называется однородной системой линейных уравнений, в противном случае система неоднородна.
Определение. n-последовательность чисел 
называется решением mхn-системы линейных уравнений, если её элементы, подставленные в заданном порядке вместо неизвестных, удовлетворяют каждому из m уравнений.
Совокупность всех решений системы называется множеством решений.
Определение. Если система имеет решение, то говорят, что она совместна или разрешена, в противном случае система не совместна (или не разрешена).
Замечание. Однородные системы линейных уравнений всегда разрешимы, так как всегда имеют тривиальное (нулевое)решение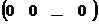 
.
При решении системы (1) возможны следующие случаи:
- система не имеет решений (система несовместна);
- система имеет решение, и оно единственное (система совместна и определена);
- система имеет множество решений (система совместна и не определена).
Решить систему – значит выяснить, совместна она или нет, и в случае совместности найти все её решения.
Пример 1. Системы линейных уравнений
1) 
; 2) 
; 3) 
.
имеют решения:
1) 
.(система совместна и определена);
2) 
(система не совместна);
3) 
, где С – любое действительное число (система совместна и не определена)
Геометрическая интерпретация решения:
- система совместна и определена – прямые, соответствующие уравнениям системы, пересекаются в одной точке;
- система несовместна – прямые, соответствующие уравнениям системы параллельны (не пересекаются);
- система совместна и не определена – прямые совпадают.
Матричный метод решения системы линейных уравнений
Рассмотрим nxn систему линейных уравнений (т.е. случай, когда число уравнений равно числу неизвестных)
(3)
С помощью матриц систему (3) можно кратко записать в виде:
, (4)
где:
–матрица коэффициентов системы размером nxn, (5)
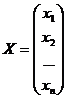– матрица-столбец неизвестных величин, (6)
– матрица-столбец свободных членов. (7).
Запись (4) называется матричной записью системы линейных уравнений (или матричным уравнением).*
В матричном виде система (3) решается с помощью обратной матрицы.
Умножив обе части уравнения (3) слева на матрицу 
,
получим:
. (8)
Выражение (8) представляет собой матрицу-столбец и является матричным решением системы (4).
Замечание: Решение (8) может быть записано только в том случае, если определитель матрицы А не равен нулю (в противном случае обратная матрица не существует).
Последовательность решения системы линейных уравнений матричным способом:
- составить для данной системы матрицы А, Х, В.
- Вычислить обратную матрицу .
- Вычислить произведение матриц 
.
- Записать ответ .
Пример 2. Решить матричным способом систему
.
Решение
1. Составим для данной системы матрицы А, Х, В.
, 
, 
.
2. Вычислим обратную матрицу .
а) Найдем определитель матрицы коэффициентов.
б) Составим присоединенную матрицу и транспонируем ее.
, 
.
в) Вычислим обратную матрицу.
.
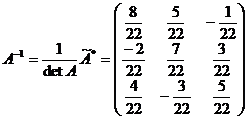3. Найдем вектор-столбец неизвестных, вычислив для этого произведение матриц .
= 
.
Ответ: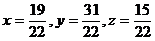 
.
Метод Крамера
Рассмотрим nxn систему линейных уравнений (3) (т.е. случай, когда число уравнений равно числу неизвестных)
.
Решение системы (8) можно записать поэлементно – отдельно для каждого неизвестного – в виде:
, 
, (9)
где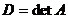 
– определитель системы (или главный определитель), составленный из коэффициентов системы:
;
- 
– определитель (вспомогательный), который получается из определителя 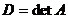заменой j-го столбца на столбец свободных членов В:
.
Формула (8) и формулы (9) называются формулами Крамера, но чаще формулами Крамера называют именно формулы (9).
Теорема Крамера
1. Если определитель системы n линейных уравнений с n неизвестными отличен от нуля 
то система совместна и имеет единственное решение Х, которое определяется по формулам:
; , .
2. Если определитель системы 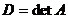равен нулю, а хотя бы один из вспомогательных определителей отличен от нуля, то система несовместна (не имеет решений).
3. Если все определители системы равны нулю 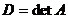= = 0, , то система либо не имеет решений, либо имеет бесконечное множество решений (если имеет хотя бы одно решение).
Пример 3. Решить систему с помощью формул Крамера
.
1). Вычислим определители: 
,
, 
, 
.
2). Так как главный определитель системы отличен от нуля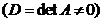 
, то система имеет единственное решение, которое может быть найдено по формулам Крамера:
, 
, 
.
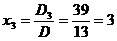Ответ: 
или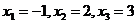 
.