ИЗ ЧЕТЫРЕХЗНАЧНЫХ ЧИСЕЛ, ПРЕДСТАВЛЯЮЩИХ
ПОЛНЫЙ КВАДРАТ
Описанный ниже способ позволит устно вычислять
корни квадратные из четырехзначных чисел, но требует
от использующего этот метод определенной культуры вы-
числительных работ. Поэтому, по-видимому, целесообраз-
но остановиться на ряде общих соображений.
Рассматривая число, из которого предстоит извлечь
корень квадратный (например, 7921), можно оценить
искомое число, а иногда и сразу сказать готовый ответ
Вспомним значение квадратов первых чисел натураль-
ного ряда: 12=1; 22 = 4; 32==9; 42=16; 52 = 25; 62=36
72 = 49; 82=64; 92 = 81. Анализируя их, мы видим, что
можем по виду числа, вернее, по его последней цифре,
сказать с точностью до 2 цифр, чем оканчивается иско-
мое число. В нашем примере это будет двузначное число,
оканчивающееся либо на 1, либо на 9.
Рассматривая 2 старших разряда, мы можем точно
назвать число десятков искомого числа: 802==6400<
<7921 <902=8100. Следовательно, число десятков раd-
но 8. Итак, мы, не произведя никаких вычислений по из-
влечению корня, уже почти определили искомое число
им может быть либо 81, либо 89. (В данном конкретном
случае из соотношений 6400 много меньше 7921 и 7921
близко к 8100 можем точно сказать, что 7921=89, но
для общего рассмотрения это не типично.)
Введем в арсенал используемых нами знаний значе-
ние квадратов первого десятка двузначных чисел:
112=121; 122=144; 132=169; 142=196; 152 = 225; 162 =
^256; 172=289; 182=324; 192=361; 202=400. Обратим
внимание на то, что числа, образованные двумя послед-
ними цифрами, все между собой различаются. Этот факт
мыи будем в дальнейшем использовать.
Рассмотрим два тождества:
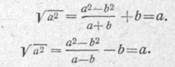
Возьмем первое тождество и потребуем, чтобы
а + Ь=100.
В этом случае нахождение корня квадратного становится
очень простым. Технику вычислений продемонстрируем
на двух примерах:

1) анализируем две последние цифры числа, из кото-
рого извлекается корень; если они образуют полный квад-
рат (как, например, в примере а), то берем это число
за Ь2:
а) Ь2 = 49, Ь = 7;
если последние две цифры не образуют полного квадра-
та, то стараемся вспомнить двузначное число, квадрат ко-
торого оканчивался бы на эти 2 цифры. При этом легче
действовать, полагаясь не на память, а на узнавание
(используя подсказку последней цифры числа):
56 — квадрат не образует,
156 — нет такого квадрата,
256 — это квадрат числа 16.
Итак, б) 62 = 256, 6=16.

2) находим (а2— Ь2): 100. Это сделать несложно, так
как либо достаточно просто отбросить два последних
знака, либо, кроме того, из числа, образованного первы-
ми двумя цифрами, надо вычесть число сотен числа Ь2:
а) (8649— 49): 100 = 86,
б) (7056 — 256): 100 = 68;
3) к полученному  результату прибавляем Ь
результату прибавляем Ь
4) в заключение обязательно осуществляем проверку
по формуле
а+Ь=100;
а) 93+ 7=100;
б) 84+16=100.
Эта проверка гарантирует правильность вычислений.
Предлагаемый алгоритм можно использовать при из-
влечении корня квадратного из чисел а2>5625 (а>75).
Для чисел 2500<а2<5625 (50<а<75) используется
формула 
Практически вычисления проводятся так же, как и в
предыдущем случае: 
62=121, 6=11, (3721 — 121): 100 = 36. Так как нам надо
разделить не на 100, а на 50, то полученный результат
умножаем на 2 36x2 = 72.
Вычитаем Ь и получаем окончательный результат
72—11=61.
Обязательно выполняем проверку:
а — Ь =50,
61 — 11 = 50 —
вычисления проведены правильно.
Наконец, при а2<2500, а<50 используем формулы

Выполняем проверку: 34+16 = 50 — вычисления про-
ведены правильно.
При беглом чтении создается впечатление запутанно-
сти и сложности метода: необходимо запоминать какие-то
граничные числа, разные формулы и т. д. На самом деле
все обстоит-гораздо проще. Посмотрим, как можно ис-
пользовать метод с минимальным запоминанием вспомо-
гательной информации:

1) решаю вопрос: 1) а<50?
2) 50<а<75?
3) 75<а<100?
Анализирую первые две цифры 38 и 25.
Считаю, что имею дело с третьим случаем;
2) нахожу Ь2: Ь2=144, Ь=12 (независимо от вариан-
тов),
3) нахожу а2—Ь2=3844— 144 = 3700,
4) так как я решил, что имею дело с третьим слу-
чаем— делю на 100 (если бы я решил, что имею дело с
первым или вторым случаем, то полученный результат
надо еще умножить на 2) 3700: 100 = 37;
5) получаю окончательный результат
а = 37+12=49;
6) выполняю проверку
49+12>=<100.
Вычисления сделаны неверно. Ошибочно вычисления
отнес к случаю 3. На самом деле имеем случай 2;
4а) возвращаюсь ко второй части процедуры 4
37X2 = 74;
5) так как а>50, то Ь надо вычитать
74—12 = 62;
6) проверка: 62—12 = 50. Вычисления проведены пра-
вильно.
Запомнить, что надо делать в процедуре 5 — склады-
вать или вычитать — очень просто. Если а<50, то до
50 надо что-то добавить. Следовательно, и в пятой проце-
дуре, и при проверке надо будет складывать. Если а>50,
то из а надо что-то вычитать, следовательно, и в пятой
процедуре, и при проверке надо будет сделать вычи-
тание.
Несколько примеров на вычисление с использованием
описанного метода:

Пр оверка: 76+24=100.
\/2601 Ь2=1, Ь = 1, а2—б2 = 2601 — 1 =2600 —случай
50<а<75.2600: 100X2=52. Ответ: 52—1=51.
Проверка: 51 — 1=50.
Следующие вычисления выполните самостоятельно
записывая только окончательный результат:
1) \/5625= 3) У4096= 5) \/2209 =
2) \/4356= 4) У9409=. 6) У12544 =
Пример 6 не.укладывается в описанную схему вычис-
лений. Но если вы поняли суть метода, то и этот пример
сможете р-ешить устно.
Ответы для проверки: 1) 75; 2) 66; 3) 64; 4) 97; 5) 47,
6) 112.