Задача о скорости химической реакции.

ТЕМА 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

ПРОИЗВОДНАЯ ФУНКЦИИ

1. Задачи, приводящие к понятию производной.
2. Определение производной. Общее правило дифференцирования.
3. Физический и геометрический смысл производной.
4. Понятие дифференцируемости функции. Связь между понятиями дифференцируемости и непрерывности.

Понятие производной является одним из основных математических понятий. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости различных процессов.

Вопрос 1. Задачи, приводящие к понятию производной

Рассмотрим некоторые задачи, приводящие к понятию производной.

Задача о скорости прямолинейного движения.

Пусть материальная точка движется прямолинейно по закону S = S(t), где t - время, а S - путь, проходимый точкой за время t. Требуется найти скорость движения точки для любого момента времени t.

Зафиксируем два момента времени t и t+∆t. К моменту времени t точка пройдет путь S(t), а к моменту времени t+∆t - путь S(t+∆t). Тогда за промежуток времени ∆t точка пройдет путь

∆S = S(t+∆t) ‒ S(t).

Отношение выражает среднюю скорость движения точки за время ∆t: .

Средняя скорость ʋ_ср зависит от значения ∆t: чем меньше ∆t, тем точнее ʋ_ср выражает скорость движения точки в данный момент времени t.

Предел средней скорости ʋ_ср при ∆t→0 называется мгновенной скоростью движения точки в момент времени t и обозначается ʋ:

или

Задача о скорости химической реакции.

Пусть дана функция m = m(t), где m – количество некоторого вещества, вступившего в химическую реакцию к моменту времени t. Приращению времени ∆t будет соответствовать приращение ∆m величины m. Отношение - средняя скорость химической реакции за промежуток времени ∆t. Предел этого отношения при ∆t→0 представляет собой скорость химической реакции в момент времени t:

Все выше рассмотренные пределы имеют одинаковый вид: везде требуется найти предел отношения приращений функции к приращению аргумента. Этот предел называют производной. Нахождение производных для различных функций и изучение свойств производных в связи со свойствами самих функций является основной задачей одного из важнейших разделов математического анализа – дифференциального исчисления.

Вопрос 2. Определение производной. Общее правило дифференцирования

Пусть функция у = f(х) определена на некотором промежутке Х. Возьмем любую точку хÎХ и дадим аргументу х приращение ∆х¹0 такое, что точка (х+∆х) ÎХ. При этом функция получит приращение ∆у = f(х+∆х) ‒ f(х).

О.2.1. Производной функции у = f(х) в точке х называется предел отношения приращения функции ∆у в этой точке к приращению аргумента ∆х при ∆х→0 (если этот предел существует).

Обозначения: .

По определению

. (1)

Если в некоторой точке х предел (1) бесконечен, то говорят, что в точке х функция f(х) имеет бесконечную производную.

Если функция f(х) имеет конечную производную в каждой точке хÎХ, то производная f′(х) является некоторой функцией, произведенной (т.е. полученной по некоторому правилу) из данной функции f(х).

Операция нахождения производной функции называется ее дифференцированием.

Из определения производной вытекает и способ ее вычисления.

Общее правило дифференцирования функции у = f(х)

1. Зафиксировав значение х, найти f(х).

2. Придав аргументу х приращение ∆х¹0 так, чтобы не выйти из области определения функции, найти f(х+∆х).

3. Найти приращение функции ∆у = f(х+∆х) ‒ f(х).

4. Составить отношение .

5. Найти предел отношения при ∆х→0: .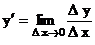

Пример 1. Найти производную функции у = 5х².

Решение

1. f(х) = 5х².

2.

3.

4.

5.