МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. М.В.Ломоносова
Механико-математический факультет
Кафедра теории вероятностей
Курсовая работа
Предельные теоремы для дискретного альтернирующего процесса
студента 3-го курса
актуарно-финансовой группы
Акчурина Руслана
Научный руководитель: к.ф.-м.н. В.В.Козлов
Москва 2016
(14.39)Пусть марковская цепь сходится к стационарному режиму и, соответственно, такова, что для некоторого состояния j имеем 
, где 
- возвратность: с вероятностью 1 марковская цепь, выходящая из состояния j, в него возвращается, и притом бесконечно часто (для тех j, что 
). Предположим, что это состояние j взято в качестве начального, и введём последовательные моменты возвращения в состояние j:
….
Марковская цепь разбивается на независимые циклы
между последовательными моментами возвращения в состояние j, эти циклы – точные вероятностные копии друг друга. Случайные моменты времени 
называются моментами восстановления марковской системы в том смысле, что, начиная с любого , система функционирует независимо от прошлого и в точности по тем же вероятностным законам, как если бы 
было начальным моментом. Процессы, обладающие указанным свойством восстановления, называются регенерирующими.
введём случайную величину 
– количество возвращений в начальное состояние (состояние j) к моменту времени n:
(фигурные скобки указывают на то, что рассматриваются события).
Заметим, что 
– это момент последнего возвращения цепи в состояние j до времени n.
Распределение вероятностей длины интервала 
:
,
где 
есть вероятность того, что марковская цепь, выходящая из состояния j, на s-ом шаге возвратится в j впервые. Существование предела 
(эргодическая теорема) эквивалентно наличию предельного распределения последовательности сл. в. 
. При этом
.
Суммируя обе стороны равенства по t с 0 до 
и считая, что предельное распределение сл. в. 
- собственное, получаем
Таким образом, 
.
Из того, что 
не зависит от i, следует, что в качестве начального состояния цепи маркова можно брать любое состояние i. Предельное распределение останется тем же.
Аналогично, рассмотрим сл. в. 
. Точно так же из соотношения
(оно получается, если из всех путей, заканчивающихся в момент n+t в состоянии j, отбросить пути, которые на временном участке от n+1 до n+t-1 попадают в состояние j) находим при t=1,2,3,…
Итак, определив последовательные моменты … попадания марковской цепи в состояние j, получаем, что сл. в. 
, независимы и одинаково распределены.
Пусть 
- произвольная последовательность, одинаково распределённых, положительных дискретных независимых сл.в. Последовательность 
называется процессом восстановления. 
определим случайные моменты :
Функция восстановления: 
.
Из представления 
получаем 
(суммы на самом деле конечные для каждого n). Так как события 
не пересекаются, то
Если снова говорить о процессе восстановления как о марковской цепи, то 
представляет собой вероятность попадания в состояние j в момент n. Значит, если марковская цепь сходится к стационарному режиму, то 
. Это утверждение носит название теоремы восстановления.
Обозначим 
, из соотношения 
имеем
Но 
, так что при 
.
где E(x) есть ф.р. вероятностного распределения, сосредоточенного в нуле. Таким образом, 
(14.40)Пусть теперь функция восстановления удовлетворяет соотношению
Выведем отсюда, что
Пользуясь ФПВ по 
:
расписываем неравенство и рассматриваем разницу 
:
Возьмём такое J, что фиксированных малых 
Тогда для суммы 
, учитывая, что 
– ограниченная последовательность, т.е. существует константа 
, имеем:
Ведь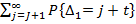 
- это хвост сходящегося ряда, 
можно взять предыдущее.
Таким образом, считая n достаточно большим:
Понятно, что сверху эта сумма так же ограничена этим же числом.
Получили: 
(Новое)Пусть 
- независимые случайные величины, причём 
одинаково распределены и 
одинаково распределены между собой. Рассмотрим теперь процесс 
, принимающий значения 0 и 1, 
. Процесс начинается в нуле и переходит в состояние 1 через время 
, затем снова переходит в состояние 0 через время 
и т.д. Таким образом, сл.в. 
– это время, которое процесс находится в 0, а 
– в 1. Введём ещё такие сл.в.:
, …, 
, … - н.о.р.
– момент n-го возвращения процесса в состояние 0
– количество возвращений процесса в состояние 0 к моменту времени 
- перескок
Мы интересуемся предельным распределением вероятности того, что процесс в момент времени n находится в состоянии 1 и перескок больше k. Найдём вероятность 
и, соответственно, её предел при 
.
Применяя ФПВ по значениям , сначала найдём вероятность того, что процесс в момент n находится в состоянии 1:
Распишем член этого ряда, воспользуемся условием 
и избавимся от него:
Возвращаемся к сумме (1), подставляем вместо каждого члена ряда его выражение через сумму, меняем порядок суммирования и суммируем по k, получаем:
где 
- функция из предыдущей задачи
Теперь нужно посчитать стремление этой суммы при . Пользуясь ФПВ по значениям сл.в. , расписываем вероятность 
:
Подставляем эту сумму вместо вероятности :
Найдём внутреннюю сумму: возьмём такое J, что фиксированных малых 
:
Необходимо напомнить, что:
1) 
2) 
Пользуясь ограниченностью последовательности константой С и тем, что 
- это хвост сходящегося ряда имеем:
Таким образом, считая n достаточно большим, разбиваем внутреннюю сумму (2) на две суммы и пользуемся особенностью выбора J:
Понятно, что сверху эта сумма так же ограничена этим же числом.
Значит,
Теперь вернёмся к вероятности: 
Проведя абсолютно аналогичные выкладки, имеем лишь следующую разницу с уже вычисленной вероятностью и её пределом:
– теперь нужно найти предел этой суммы при 
Так же, как и с предыдущим пределом, распишем неравенство 
в сумму из равенств и разобьём полученную внутреннюю сумму на две суммы; n при этом считаем достаточно большим:
Возьмём такое J, что фиксированных малых 
1) 
2) 
Пользуясь ограниченностью последовательности константой С и тем, что 
- это хвост сходящегося ряда имеем:
Значит, учитывая специально выбранное J, внутренняя сумма 
равна:
Таким образом, зная, что сверху внутренняя сумма ограничена числом 
, получили равенство этой суммы числу :
