Расчетно-графическое задание
По дисциплине
Исследование операций и системный анализ.
Вариант
Выполнил:
Студент: Волков А.
Группа: СД-91
Факультет: ЛА
Проверила: Третьякова Н.В.
Новосибирск 2011
Линейное программирование. Основная задача линейного программирования (ОЗЛП).
Имеется задача Линейного программирования с ограничениями-неравенствами 
:
требуется дать этой задаче геометрическую интерпретацию и построить область допустимых решений 
, если она существует, и найти оптимальное решение
Решение:
приведём систему к стандартному виду:
В нашем случае число переменных 
, а число независимых уравнений 
, при этом 
Тогда, можем 2 из этих 6 переменных, например 
, выбрать в качестве свободных, а остальные 4 сделать базисными и выразить их через свободные. Получим 
уравнений:
Дадим задаче ЛП геометрическую интерпретацию. По осям 
и 
будем откладывать значения свободных переменных 
и 
. Отметим это штриховкой, обозначающей «допустимую сторону» каждой координатной оси.
Остальные переменные 
также должны быть неотрицательными, т.е. 
Изобразим эти условия геометрически. Возьмем
Положим величину 
Получим уравнение 
. Из этого уравнение находим 
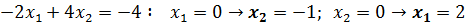
Это уравнение прямой. на этой прямой 
По одну сторону от нее 
, а по другую 
(это определяется коэффициентами уравнения). Отметим штриховкой ту сторону прямой 
по которую 
Положим величину 
.
Получим уравнение 
Положим величину 
Получим уравнение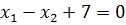 
Положим величину 
Получим уравнение 
Таким же образом, мы получим еще 2 прямых, а после этого можем найти область допустимых решений и выделим жирной линией (рис.1).
Геометрическая интерпретация представлена на рис. 1.
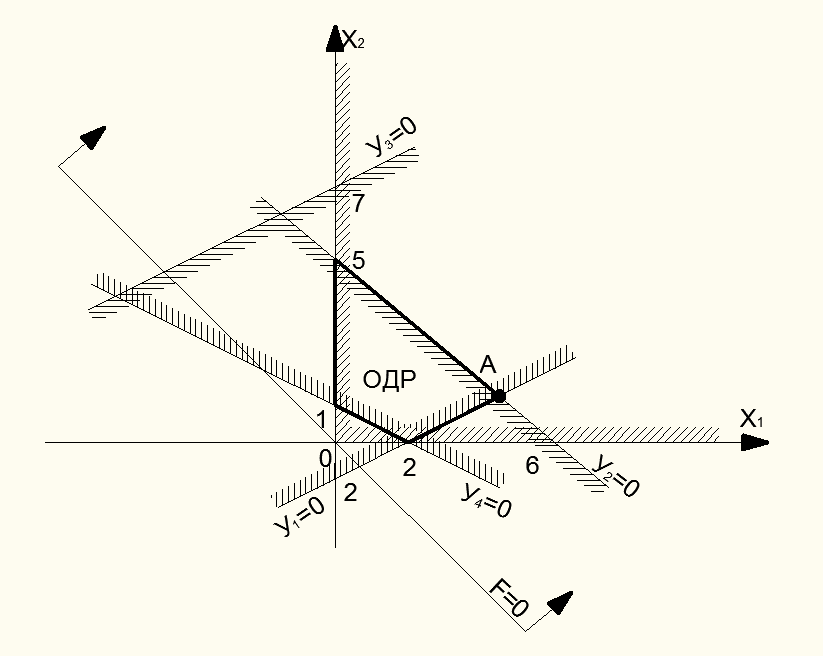
Рис.1
Пусть имеется область допустимых решений ОДР (рис. 1) и основная прямая 
; известно (указано стрелками) направление убывания линейной функции F. При перемещении основной прямой в направлении, указанном стрелками, линейная функцияF будет убывать.
Очевидно, наименьшего значения она достигнет, когда прямая будет проходить через крайнюю точку ОДР, наиболее удаленную от начала координат в направлении стрелок (точку А). Координаты этой точки А (
и 
) и определяют оптимальное решение ОЗЛП. Зная оптимальные значения свободных переменных 
и 
, можно найти, подставляя их в уравнения (3), оптимальные значения базисных переменных:
Приравняем к 0 первое и второе уравнение из системы (3)
(4)
отсюда найдем 
- оптимальное и, подставляя в первое уравнение, получим 
- оптимальное.
Зная оптимальные значения свободных переменных и , можно найти, подставляя их в уравнения (3), оптимальные значения базисных переменных
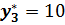
а также оптимальное (min) значение линейной функции F:
Ответы
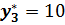
Симплекс-метод решения задачи Линейного программирование.
Для нахождения решения задач ЛП при числе свободных переменных 
применяются не геометрические, а вычислительные методы. Из них наиболее универсальным является симплекс-метод.
Имеется задача линейного программирования с ограничениями-неравенствами (1).
(1)
требуется найти оптимальное решение.
Решение:
(2)
Форму записи уравнений (2) будем называть стандартной.
Записываем условие (2) в виде стандартной таблицы (табл. 1). В табл.1имеется отрицательный свободный член –2 в строке 
. Согласно правилу выбираем любой отрицательный элемент этой строки. Мы выбрали разрешающий столбец 
.
В качестве «кандидатов» на роль разрешающего элемента рассмотрим все те элементы этого столбца, которые одинаковы по знаку со своим свободным членом: это будет -2
Таблица 1
(нуль в качестве разрешающего элемента быть не может).
Таблица 2
Таблица 3
Таблица 4
| с.ч | Y1 | Y2 | |
| F | -15 | -0,375 | -2,25 |
| X1 | 0,25 | ||
| Y4 | 0,00 | ||
| Y3 | 0,38 | ||
| X2 | -0,125 | 0,25 |
В таблице 4 в строке F нет ни одного положительного элемента, значит, оптимальное решение достигнуто. Оно будет:
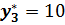
При этих значениях переменных линейная функция F достигает минимума
Алгоритм преобразования 
стандартной таблицы сводится при этом к следующим операциям:
1. Выделить кружком в таблице разрешающий элемент 
. Вычислить его обратную величину 
и записать в нижней части той же ячейки (в правом нижнем углу).
2. Все элементы разрешающей строки (кроме самого 
) умножить на 
, результат записать в нижней части той же ячейки.
3. Все элементы разрешающего столбца (кроме самого 
) умножить на (
); результат записать в нижней части той же ячейки.
4. Выделить рамкой в разрешающей строке все верхние числа (т.е. прежние элементы), за исключением самого разрешающего элемента, а в разрешающем столбце выделить все нижние числа (новые элементы), за исключением самого разрешающего элемента.
5. Для каждого из элементов, не принадлежащих ни к разрешающей строке, ни к разрешающему столбцу, записать в нижнюю часть ячейки произведение выделенных чисел, стоящих в том же столбце и в той же строке, что и данный элемент.
6. Переписать таблицу, заменив:
а) 
на 
и обратно;
б) элементы разрешающей строки и столбца – числами, стоящими в нижних частях тех же ячеек;
в) каждый из остальных элементов – суммой чисел, стоящих в верхней и нижней части той же ячейки.
Правило нахождения оптимального решения ОЗЛП симплекс-методом:
1. Если все свободные члены (не считая строки L) в симплекс-таблице неотрицательны, а в строке L (не считая свободного члена) нет ни одного положительного элемента, то оптимальное решение достигнуто.
2. Если в строке L есть положительный элемент, а в столбце, соответствующем ему, нет ни одного положительного элемента, то линейная функция L не ограничена снизу и оптимального решения не существует.
3. Если в этом столбце есть положительные элементы, то следует произвести замену одной из свободных переменных на одну из базисных, причем в качестве разрешающего надо взять тот элемент этого столбца, для которого отношение к нему соответствующего свободного члена минимально.