Пути. Циклы. Цепи в графах

Лекция 7-8. Оптимизация на сетях и графах

Элементы теории графов. Основные понятия и определения

Теория графов - это область дискретной математики, особенностью которой является геометрический подход к изучению объектов. Теория графов находится сейчас в самом расцвете. Обычно её относят к топологии (потому что во многих случаях рассматриваются лишь топологические свойства графов), однако она пересекается со многими разделами теории множеств, комбинаторной математики, алгебры, геометрии, теории матриц, теории игр, математической логики и многих других математических дисциплин. Основной объект теории графов-граф и его обобщения.

Первые задачи теории графов были связаны с решением математических развлекательных задач и головоломок (задача о Кенигсбергских мостах, задача о расстановке ферзей на шахматной доске, задачи о перевозках, задача о кругосветном путешествии и другие). Одним из первых результатов в теории графов явился критерий существования обхода всех ребер графа без повторений, полученный Л. Эйлером при решении задачи о Кенигсбергских мостах. Вот пересказ отрывка из письма Эйлера от 13 марта 1736 году: ” Мне была предложена задача об острове, расположенном в городе Кенигсберге и окруженном рекой, через которую перекинуто 7 мостов. Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост.

И тут же мне было сообщено, что никто еще до сих пор не смог это проделать, но никто и не доказал, что это невозможно. Вопрос этот, хотя и банальный, показался мне, однако, достойным внимания тем, что для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство. После долгих размышлений я нашел лёгкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода тотчас же определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может“.

Кенигсбергские мосты схематически можно изобразить так:

При изучении бинарных отношений под графом понималась схема, состоящая из точек – вершин графа, и связывающих эти точки попарно отрезков или дуг – ребер графа. Такая схема позволяет удобно и наглядно задавать бинарные отношения на конечном множестве. Однако помимо иллюстративных целей граф может служить удобной математической моделью при описании самых разнообразных объектов.

Например, графом может быть представлен план работ по реализации какого-либо проекта, при этом вершинами графа являются этапы работ, а ребра указывают последовательность выполнения этапов. С помощью такого графа удобно вычислять время реализации проекта, что достаточно непросто, если некоторые работы могут выполняться параллельно, а также резервы времени на каждом этапе.

В виде графа может быть представлена блок-схема программы: вершины – блоки, ребра – разрешенные переходы от одного блока к другому. Такое изображение позволяет найти кратчайший путь от одного блока к другому.

Представление графом сетей нефтепроводов, сетей связи, транспортных сетей позволяет рассчитывать их пропускную способность и выявлять "узкие места". Существует также множество логических и занимательных задач, решение которых предполагает использование графов.

Графом G называют пару множеств (V, E), где V – множество вершин графа (точек); E – семейство ребер графа (отрезков или дуг, соединяющих вершины в пары):

V={v₁,v₂,v₃,…,v_n};

E={e₁, e₂, e₃,…,e_m };

e_i =(v_j,v_k) – i -е ребро графа G; v_j,v_k – концевые вершины этого ребра (i =1,2,3,…, m; v_j, k =1,2,…, n).

 

Пример графа:

 

То есть, элементы множества V называются вершинами графа. Элементы множества E - ребрами графа. Ребра вида (v,v), в которых первый элемент равен второму элементу, называются петлями. Или, если концевые вершины ребра совпадают, то ребро образует петлю (дугу, начало и конец которой совпадают).

 

Если пара (v₁,v₂) Î E − ребро, то v₁ и v₂ называются концами этого ребра. В этом случае вершины v₁ и v₂ называются смежными в графе, а само ребро (v₁, v₂) называется инцидентным вершинам v₁ и v₂.

Пусть в графе есть ребро (v₁,v₂), тогда можно считать, что в нем есть ребро (v₂,v₁). Если при этом указанные ребра не различать (т. е. (v₁,v₂)= (v₂,v₁), пары считаются неупорядоченными), то граф называется неориентированным графом.

Если в графе есть несколько одинаковых ребер вида (v₁,v₂), то такое ребро называют кратным.

В дальнейшем мы будем рассматривать неориентированные графы без кратных ребер и без петель. Таким образом, каждое ребро (v₁,v₂) может присутствовать в графе только один раз, и считаем, что ребер вида (v,v) в графе нет, ребра (v₁,v₂) и (v₂,v₁) совпадают. Такие графы называются простыми.

Графы можно изображать графически. Вершины изображаются точками, ребра изображаются линиями соединяющие соответствующие вершины.

 

Приведем пример графа, имеющего четыре вершины и восемь ребер, одно из которых – петля (e₈), приведен на рис. 6.1. Ребра e₄, e₅ кратные или параллельные друг другу, так же как и ребра e₆ и e₇.

 

Фиксируем на плоскости произвольным образом п точек и произвольным образом дадим им в качестве имен имена вершин данного графа. В итоге на плоскости возникнут точки, обозначенные как 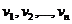. Затем для каждой пары точек 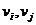таких, что 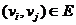, проведем отрезок прямой, соединяющий точки 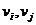. В результате таких действий возникнет некоторый рисунок, который и называется геометрической интерпретацией графа. Заметим, что одному и тому же графу соответствует много рисунков, которые могут быть его геометрическими интерпретациями. Вот два рисунка, каждый из которых является геометрической интерпретацией графа, приведенного выше в качестве примера:

3

2 4 2 5 4

 

 

1 5 1

Рис.1 Рис.2

 

Число вершин графа называют порядкомграфа и обозначают ½V½= n. Граф будем обозначать парой G = (V, E).

Число вершин графа называют порядком графа и обозначают ½V½= n. Граф будем обозначать парой G = (V, E).

Граф G называется помеченным, если его вершинам приписаны числа 1, 2, …, п, где п − порядок графа.

Граф можно задать с помощью матрицы размера n x n: А(G)=[a_ij], где

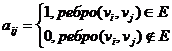
эта матрица симметрична с нулями по главной диагонали. Она называется матрицей смежностей графа G = (V, E).

 

В приведенном выше примере графа матрица смежностей такова:

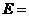
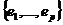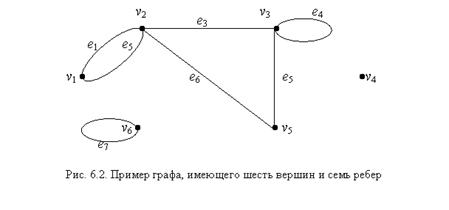
Сопоставим графу G = (V, E) еще одну матрицу. Будем считать, что - по-прежнему множество вершин и пусть - множество ребер. Определим матрицу размера n x p: B(G)=[b_ij], 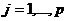следующим образом:

Введенная так матрица B(G) называется матрицей инциденций данного графа. Очевидно, вид матрицы смежностей и вид матрицы инциденций существенно зависят от того, как именно занумерованы вершины и ребра. Если в приведенном выше примере графа считать, что

,

то матрица инциденций будет такой:

.

В каждом столбце матрицы инциденций всегда ровно две единицы, остальные элементы равны нулю. Если в графе все вершины имеют степень ноль, то матрицы инциденций - нулевая.

 

 

Ребра графа могут быть ориентированными или неориентированными. Граф на рис. 6.1 имеет неориентированные ребра. При изучении бинарных отношений были использованы графы, все ребра которых ориентированы. Такие графы называют ориентированными графами или орграфами.

Если вершины v_i и v_j (i≠j) соединены ребром e_k= (v_i,v_j), то их называют смежными вершинами. Если ребра e_k, e_l имеют общую вершину, то их называют смежными ребрами. Если вершина v_i является концом ребра e_j, то v_i называют вершиной, инцидентной ребру e_j, а e_j – ребром, инцидентным вершине v_i.

 

Степенью вершины графа называется число инцидентных ей ребер, (число вершин смежных этой вершине, число ребер выходящих из этой вершины, число ребер входящих в нее). Обозначают степень вершины v через deg (v).

Вершина называется изолированной, если её степень равна нулю, и называется концевой (висячей), если её степень равна единице. Вершина называется доминирующей, если она смежная со всеми вершинами графа.

 

Сумма степеней всех вершин графа есть четное число.

в любом графе число вершин с нечетными степенями четно.

 

 

 

Пути. Циклы. Цепи в графах

 

Пусть G = (V, E) некоторый граф. Путем (маршрутом) в графе G, соединяющим вершины v₁ и v_n, называется любая чередующаяся последовательность вершин и ребер вида v₀,e ₀,v₁,e₁,v₂,e ₂…v_n-1,e _n-1,v_n, в которой каждое ребро e_i инцидентно вершинам v_i и v_i+1.

Путь называется замкнутым, если его начальная и конечная вершины совпадают.

Путь называется цепью, если все его ребра различны.

Цепь называется простой, если все ее вершины различны.

Замкнутая цепь называется циклом.

Цикл называется простым, если его вершины не повторяются.

Вот схематическое изображение простого цикла:

 

 

А вот схематическое изображение цикла, не являющегося простым:

 

Для пути v₀, e ₀ ,v₁, e₁, ….v_n число ребер n называется длиной пути.

Две вершины графа могут быть связаны некоторым путем: их называют связанными. Например, в графе

a ₁

 

a ₂ a ₃. a ₄

 

a ₅

 

вершины a ₃ и a ₅ связаны (путем ), а вершины a ₄ и a ₁ нет.

 

Простой граф – это граф, не содержащий петель и кратных ребер.

Граф называется связным, если для любой пары его вершин существует соединяющая их простая цепь. Т.о. граф связен, если из любой его вершины можно прийти к любой другой. Таким образом, выше приведен пример графа несвязного. Связной компонентой графа называется такой его подграф, который является сам по себе графом связным и при этом совпадающим с любым другим содержащим его связным подграфом. Таким образом, связный граф обладает единственной связной компонентой - это он сам. А вот пример графа с тремя связными компонентами (имена вершин не имеют значения):

 

 

Компонентой связности графа называется максимальный (по числу вершин и ребер) связный подграф этого граф.

Каждый граф или сам является компонентой связности или распадается на компоненты. Граф, содержащий хотя бы две компоненты связности, называется несвязным. Связный граф состоит из одной компоненты связности.

Граф называется эйлеровым, если он содержит цикл, проходящий через все ребра этого графа по одному разу. Такой цикл называется эйлеровым циклом.

Вот пример эйлерова графа:

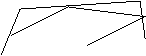А вот пример графа, не являющегося эйлеровым:

 

 

Обходы графа

Во многих задачах, решаемых с использованием графов, требуется проложить маршрут от одной вершины графа к другой или обойти все его вершины, учитывая те или иные ограничения.

Смысл такой задачи на интуитивном уровне ясен, но требуется уточнить понятия, используемы при решении подобного рода задач.

Прежде всего, уточним термины "маршрут", "цепь", "цикл" и "путь". Эти четыре понятия находятся в следующем соотношении: пути и циклы – это особые виды цепей, цепь – особый вид маршрута.

Маршрут – это последовательность вершин и ребер графа, следуя по которым, можно попасть из одной его вершины в другую.

Цепь – это маршрут без повторяющихся ребер.

Путь – это цепь, все вершины которой (за исключением, быть может, начальной и конечной) различны.

Цикл – это цепь, у которой совпадают начальная и конечная вершины, а все остальные различны.

Пример.

Можно составить следующие маршруты из А в С в графе G:

М1: А – е1 – В – е3 – С (путь);

М2: А – е2 – Е – е6 – Д – е7 – Д – е6 – Е – е5 – С (не цепь);

М3: А – е1 – B – е3 – C – е5 – Е – е4 – С (цепь, но не путь).

Циклы:

А – е1 – В – е3 – С – е4 – Е – е2 – А;

Е – е4 – С – е5 – Е;

Д – е7 – Д.

Граф называют связным, если из каждой его вершины существует путь в любую другую его вершину. Граф, рассмотренный в примере, является, связным. Если удалить из него ребро, то он потеряет связность и распадется на компоненты: одна из компонент будет содержать вершину Д и петлю, вторая компонента – вершины А,В,С,Е, связанные между собой всеми оставшимися ребрами.

Для представления данных в алгоритмах на дискретных структурах часто используются графы, которые называются деревьями.

Деревом называют связный неорграф, не содержащий циклов.

На рис. 6.8 показано, так называемое, корневое дерево. Одна из вершин корневого дерева (вершина 1) выделена, ее называют корнем дерева. Оставшиеся вершины разбиты на поддеревья (поддерево с вершинами 2,5,6 и поддерево 4,7,8,9). Вершины 5,6,3,7,8,9 называют листьями дерева. Несвязный неорграф, компонентами которого являются деревья, называют лесом.

Если граф связный, но не является деревом, в нем всегда можно выделить часть, включающую все вершины и образующую дерево. Такую часть графа называют остовом графа. Если граф несвязен, то можно превратить в дерево каждую его компоненту. Полученная совокупность деревьев носит название остовного леса.

Вообще говоря, в графе можно выделить несколько различных остовов. Каждый из них будет являться деревом, включающим все вершины графа, а следовательно, число ребер любом из остовов будет на единицу меньше числа вершин графа. Если выделен какой-либо остов, то все ребра графа, не вошедшие в этот остов, образуют коостов, соответствующий данному остову.

Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

 

Пусть G связный граф. Тогда остовное дерево графа G (если оно существует) должно содержать n(G) – 1 ребер. Таким образом, любое остовное дерево графа G есть результат удаления из G ровно m(G)-(n(G)-1)=m(G)-n(G)+1 ребер.

 

На рис. 6.9 показан пример выделения деревьев, остовов и коостовов из графа.

 

 

Деревья и циклы

 

Определение. Граф G называется деревом, если он является связным и не имеет циклов. Граф G, все компоненты связности которого являются деревьями, называется лесом.

 

Пример 86.

 

Граф G1 является деревом (рис.38). Граф G2 является лесом (рис. 38), он содержит три связные компоненты, каждая из которых является деревом.

 

Следующие утверждения эквивалентны:

 

граф G есть дерево;

граф G является связным и не имеет простых циклов;

граф G является связным и число его ребер ровно на единицу меньше числа вершин;

любые две различные вершины графа G можно соединить единственной (и притом простой) цепью;

граф G не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один (с точностью до направления обхода и начальной вершины обхода) и притом простой цикл (проходящий через добавляемое ребро).

 

Утверждение. Если у дерева G есть, по крайней мере, одно ребро, то у него обязательно найдется висячая вершина.

 

Утверждение. Пусть G – дерево. Тогда любая цепь в G будет простой.