Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида: {(a11x1+a12x2+…+a1nxn=b1) (a21x1+a22x2+…+a1nxn=b2)….. (am1x1+am2x2+…+amnxn=bm), где числа aij, i=1..m, j=1..n называются коэффициентами системы, числа bi – свободными членами. Такую систему удобно записывать в компактной матричной форме AX=B. А – матрица коэффициентов системы, называемая основной матрицей. X – вектор столбец из неизвестных xj. В – вектор-столбец из свободных членов bi.
Расширенной матрицей системы называется матрица А системы, дополненная столбцом свободных членов.
Решением системы называется n значений неизвестных x1=c, x2=x2,…,xn=cn, при подстановке которых все уравнения системы обращаются в верные равенства. Системы уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Совместная система называется определённой, если она имеет единственное решение, и неопределённой, если она имеет более одного решения. В последнем случае каждое её решение называется частным решением системы.
Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти её общее решение.
Две системы н называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Система линейных уравнений называется однородной, если все свободные члены равны нулю.
Обратная матрица
Б удем рассматриват квалратные матрицы n-ого порядка
ОПР.
Матрица В назыв оьратной матрице А если АВ=ВА=Е
Обозначается А^(-1)
Можно доказать что чтобы матрица имела обратную необходимо и достаточно чтобы d(A) не =0 (определитель)
Правило:
Чтобы вычислить обратную матрицу нужно: заменить в матрице А все элементы их алгбраического дополнения
Протранспонир полученную матрицу
Поделить на определитель исходной матрицы.
ПРИМЕР А =(37) A^(v)= (4 -2) А^(-1)=-1/2*(4 -7)=1/2*(-4 7)
(2 4) (-7 3)
(-2 3) (2 -3)
A^(vt) =(4 -7) d(A) = 3*4 –7*2=-2
(-2 3)
Ранг матрицы
Рангом матрицы называется число элементов максимально линейно независимой подсистемы системы её столбцов.
Рангом матрицы называется наибольший из порядков миноров данной матрицы, отличных от нуля.
Минор, порядок которого определяет ранг матрицы, называется базисным.
Ранг ненулевой матрицы равен наивысшему порядку её отличного от нуля минора.
РАНГ МАТРИЦЫИ ЕГОВЫЧИСЛЕНИЕ.
Рассмотрим произвольную матрицу размером MxN:


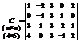
(MxN) (4x5) (1Ј kЈ N, 1Ј k Ј N)
Выделим какие либо K строк и K столбцов, а остальные вычеркнем.
Определитель, лежащий на пересечении оставшихся строк и столбцов называется минором.
У матрицы С 5 миноров высшего порядка. Много миноров 3-го и 2-го порядка и 20 миноров 1-го порядка. Некоторые из них равны 0, некоторые отличны от 0.
Пусть R такое число, что все миноры порядка R+1=0 или их вообще нет, а среди миноров порядка R есть хотя бы один неравный 0, тогда число R называется рангом матрицы, так у матрицы С все миноры 4-го порядка равны 0, а минор 3-го порядка, стоящий в левом верхнем углу не равен 0, значит ранг матрицы С:
Rg C= R= 3.
Опр. Рангом матрицы называется наивысший порядок неравных нулю миноров. Для вычисления ранга имеется 2 метода:
- метод окаймляющих миноров
метод элементарных преобразований.