Перейдём теперь к рассмотрению методов построения шкалы предпочтений, получаемой при экспертном высказывании суждений о мере различия между сравнительными объектами.
В МАИ для этих целей применяются метод парных сравнений. Если для сравнения выбрано n(А1,А2,…,Аn) объектов, то результаты сравнений заносятся в квадратную n – мерную матрицу вида:
| A1 | A2 | … | Aj | … | An | |
| А1 | a11 | a12 | … | a1j | … | a1n |
| А2 | a21 | a22 | … | a2j | … | a2n |
| … | … | … | … | … | … | … |
| Аi | ai1 | ai2 | … | aij | … | ain |
| … | … | … | … | … | … | … |
| Аn | an1 | an2 | … | anj | … | ann |
Элементом этой матрицы аij является мера предпочтения Аi объекта по сравнению с Аj объектом. Таким образом i–я строка матрицы показывает меру предпочтения i–го объекта над другими (n-1) объектами n над самим собой. Мера предпочтения выражается экспертом в шкале Саати и принимает значения от 1 до 9, если объект Аi предпочтительнее или более важен чем объект Аj. В случае, когда i=j, мера предпочтения равна 1, то есть диагональные элементы матрицы парных сравнений всегда равны 1. Следует учитывать, что для матрицы парных сравнений выполняются следующие условия:

Это означает, что если по шкале Саати объект Аi предпочтительнее Aj и аij=5, по мере предпочтения Аj объекта по отношению к Аi т.е.  .
.
Таким образом, экспертом заполняется только верхняя наддиагональная часть матрицы парных сравнений (заштрихованная) и матрица приобретает следующий вид (например для четырёх сравнительных объектов).
| А1 | А2 | А3 | А4 | |
| А1 | а12 | а13 | а14 | |
| А2 | 1/а12 | а23 | а24 | |
| А3 | 1/а13 | 1/а23 | а25 | |
| А4 | 1/а14 | 1/а24 | 1/а34 |
Экспертная оценка сравнительной важности объектов может осуществляться в двух ситуациях. Первая ситуация имеет место, если свойства сравниваемых объектов имеет одну природу и одинаковые единицы измерения. Тогда если мера свойств Аi равна ωi, а мера объекта Аj равна ωj, то мера предпочтения объекта Аi по сравнению с объектом Аj равна 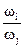 . Матрица предпочтений сформирована для такой ситуации является согласованной.
. Матрица предпочтений сформирована для такой ситуации является согласованной.
В общем случае над согласованностью подразумевается то, что при наличии основного массива необработанных данных, все другие данные могут быть логически получены из них. Если сравнивается n объектов, то достаточно (n-1) суждения, в которых сравниваемые объекты представлены, по крайней мере, один раз.
Рассмотрим для примера матрицу парных сравнений для трёх объектов (А1,А2,А3). Путём измерения было получено, что объект А1 в 3 раза превосходит объект А2  и в 6 раз объект А3,
и в 6 раз объект А3,  .
.
При n=3 достаточное число сравнений равно n-1=3-1=2. Заполняем матрицу и получаем.
| А1 | А2 | А3 | |
| А1 | |||
| А2 | 1/3 | ||
| А3 | 1/6 | ½ |
Неизвестные суждения получим из системы уравнений
А1=3А2 А1=6А3
Откуда 3А2=6А3 или А2=2А3 и А3=1/2А2.
Такая согласованность называется полной, которая включает порядковую согласованность или свойство транзитивности (если Аi предпочтительнее Аj, а Аj предпочтительнее Ак, то Аi предпочтительней Ак), а также кординальную согласованность (аij·аjk=aik).
Вторая ситуация, наиболее распространённая, состоит в том, что свойства сравниваемых объектов могут быть оценены только по шкале Саати. Например влияние капитала и политики на экономику страны.
В этом случае добиться полной согласованности матрицы парных сравнений невозможно.
Естественно после экспертных оценок по методу парных сравнений поставить вопрос о степени согласованности полученных оценок.
В качестве меры согласованности рассматривают два показателя:
- индекс согласованности (ИС);
- относительная согласованность (ОС).
Из теории матриц известно, что согласованность обратно симметричной матрицы эквивалентна требованию равенства её максимального собственного значения λmax и числа сравниваемых объектов n (λmax=n).
Поэтому в качестве меры согласованности рассматривают нормированное отклонение λmax от n, называемое индексом согласованности:
 (1)
(1)
Для того чтобы оценить, является ли полученное согласование приемлемым или нет, его сравнивают со случайным индексом СИ.
Случайным индексом называют индекс согласованности, рассчитанный для квадратной, положительной n-мерной обратно симметричной матрицы, элементы которой сгенерированны случайным образом (датчиком равномерно распределенных случайных чисел в интервале 1-9). Для матрицы с фиксированным значениям n индекс рассчитывается как среднее значение для выборки N=100. Ниже приведена таблица 2. для величин случайного индекса для различных матриц порядка от 1 до 15.
Таблица 2.
| Порядок матрицы | |||||||||||||||
| СИ | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 | 1,51 | 1,54 | 1,56 | 1,57 | 1,59 |
Получив в результате расчёта по формуле (1.) индекс согласованности и выбрав по таблице 2. случайный индекс для заданного порядка матрицы, рассчитывают отношения согласованности (ОС):
 (2.)
(2.)
Если величина ОС < 1, то степень согласованности считается приемлемой.
Если ОС > 0,1 эксперту рекомендуется пересмотреть свои суждения. Для этого необходимо выявить те позиции в матрице суждений, которые вносят максимальный вклад в величину отношения согласованности, и попытаться изменить меру несогласованности в меньшую сторону на основе более глубокого анализа вопроса.
Анализ результатов экспертных оценок заключается в математической обработке матрицы суждений с целью получения вектора приоритетов сравниваемых объектов. С математической точки зрения задача сводится к вычислению компоненты главного собственного вектора, который после нормализации становится вектором приоритетов.
| A1 | A2 | … | An | Главный собственный вектор | Вектор приоритетов | |
| А1 | a11 | a12 | … | a1n | V1 | P1 |
| А2 | a21 | a22 | … | a2n | V2 | P2 |
| … | … | … | … | … | … | … |
| Аn | an1 | an2 | … | ann | Vn | Pn |
Компонента главного собственного вектора вычисляется как среднее геометрическое значение в строке матрицы:
 (7.3)
(7.3)
Компонента вектора приоритетов вычисляется как нормированное значение главного собственного вектора:
