Часть 2. Матрицы
Определение. Матрицей называется прямоугольная таблица чисел.
Понятие матрицы, как и операции над ними, имеет простой практический смысл. Действительно, очень часто производственные и иные показатели своей деятельности люди записывают по столбцам и по строчкам, т.е. используют матрицы.
В общем виде матрицу записывают так:
А = 
,
где 
- 
элемент матрицы А, стоящий на пересечении строки с номером 
и столбца с номером 
. Матрица А имеет 
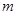строк и
столбцов и в этом случае говорят, что она имеет размер 
.
Если 
, то матрицу называют квадратной.
Нулевая матрица – это матрица, в которой все элементы равны нулю.
Единичная матрица – это квадратная матрица, в которой все элементы главной (правой) диагонали равны единице, а остальные ее элементы равны нулю.
Диагональная матрица – это матрица, в которой все элементы, не принадлежащие главной диагонали, равны нулю.
Треугольная матрица – это матрица, в которой все элементы, расположенные ниже (выше) главной диагонали, равны нулю.
Однотипные матрицы – это матрицы, в которых одинаковое количество строк и количество столбцов, т.е. имеющие одинаковый размер.
Симметрическая матрица – это матрица, в которой элементы, симметричные относительно главной диагонали, равны между собой.
Линейные операции над матрицами и их свойства
Под линейными операциями над матрицами понимают: сложение и вычитание матриц, а также умножение матрицы на число. Первые две операции выполнимы только над однотипными матрицами, третья – всегда.
В дальнейшем мы будем использовать следующие обозначения:
,… – матриц A, B, C, X, Y,…соответственно.
Определение. Суммой матриц А и В называется матрица С такая, что 
. Т.е. при сложении однотипных матриц их элементы, стоящие на одинаковых местах, складываются.
Определение. Разностью матриц А и В называется матрица С такая, что 
. Т.е. при вычитании однотипных матриц их элементы, стоящие на одинаковых местах, вычитаются.
Определение. Произведением числа 
на матрицу А называется матрица В такая, что 
. Т.е. при умножении числа на матрицу надо все ее элементы умножить на это число.
Примеры.
1) 
;
2) 
;
3) 2 
=
= 
.
Свойства линейных операций над матрицами
1) А + В = В+А;
2) (А + В) + С = А + (В + С);
3) А + О = А;
4) А + (-1)А = О;
5) (n + m)A = nA + mA;
6) (nm)A = n(mA);
7) 1 
8) n(A + B) = nA + nB.
Справедливость этих восьми свойств вытекает из того, что линейные операции над матрицами сводятся к соответствующим арифметическим операциям над числами, а они этими свойствами обладают.
Умножение и обращение матриц
Определение. Произведением матрицы А размерности 
на матрицу В размерности 
называется матрица С размерности 
такая, что
,
где 
Таким образом, для получения элемента 
надо умножить -ю строку матрицы А на 
- й столбец матрицы. Изобразим схему вычисления .
Примеры.
;
;
.
Если
A = и E = 
,
то, очевидно, A 
(считаем, что матрицы А и Е однотипные и квадратные).
Определение. Однотипные квадратные матрицы А и В называются взаимно обратными, если A 
В этом случае полагают, что B = A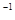 
.
Операции над матрицами удовлетворяют следующим свойствам:
1. 
(кроме случая, когда B есть степень матрицы A).
2.(A 
3. (A 
= A.
4. (A + B) 
.
5. A 
6. k 
.
7. Определитель произведения однотипных квадратных матриц равен произведению их определителей, т.е. 
.
8. (А 
) 
.
9. (A 
) 
.
10. 
.
Проиллюстрируем первое свойство на примере. Пусть
A = 
и B = 
.
Тогда
АВ = 
, ВА = 
, т.е. АВ 
ВА.
В третьем свойстве утверждается, что обратная матрица обратной матрицы есть исходная матрица. Это вполне очевидно.
В восьмом свойстве утверждается что матрица 
является обратной для матрицы 
. Это верно, так как
() 
) = 
= 
= 
= E.
Седьмое свойство справедливо на основании того, что элементы определителя, являющегося результатом произведения двух определителей одинакового размера, вычисляются по той же формуле, что и элементы произведения двух однотипных квадратных матриц. Этот факт принимаем без доказательства и проверим седьмое свойство на частном примере.
= 
=
=(
=
= 
=
= 
.
= (
.
Таким образом, седьмое свойство на этом примере выполняется. Оставшиеся свойства предлагаем читателям доказать самостоятельно.
Теорема 2.1. Обратная матрица имеет вид:
А 
.
Доказательство.
= 
= E,
так как:
Определение. Если определитель квадратной матрицы равен нулю, то она называется вырожденной. Вырожденная матрица не имеет обратную матрицу.
Пример. Для матрицы А = 
найти обратную матрицу.
Решение.
│ A │ =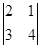 
= 8 - 3 = 5,
A11 = M11 = 4,
A12 = -M12 = -3,
A21 = -M21 =- 1,
A22 = M22 = 2,
A-1 = 
= 
.
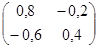Пример. Для матрицы
найти обратную матрицу.
Решение. Для решения этого примера надо найти определитель матрицы и девять алгебраических дополнений.
= 2 +2 +0 – 0 – 0 – 3 = 1. 
, 
, 
, 
, 
, 
, 
= -1, 
. Подставляя эти результаты в формулу обратной матрицы, получим
.
Элементарные преобразования матриц
Определение. Элементарными называются следующие преобразования матриц:
1) перестановка двух любых столбцов (или строк);
2) умножение столбца (строки) на любое число, отличное от нуля;
3) прибавление к столбцу (к строке) линейной комбина-
ции других строк (столбцов).
Определение. Минором k – го порядка матрицы называется определитель k – го порядка, полученный из матрицы удалением нескольких строк и нескольких столбцов.
Определение. Рангом матрицы называется максимум порядков ее миноров, отличных от нуля.
Пример. Найти ранг матрицы:
