Рассмотрим параллелепипед, построенный на трех векторах. Его объем равен:


 в Oē1ē2ē3
в Oē1ē2ē3


 (V)
(V)
Аффинное преобразование в пространстве. Выведем формулы преобразования координат вектора в пространстве. Преобразование координат точек:








Рассмотрим преобразование трех векторов



 в I Oē1ē2ē3
в I Oē1ē2ē3



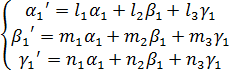
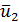



Рассмотрим V параллелепипеда, построенного на 


 - определитель матрицы АП пространства
- определитель матрицы АП пространства
 (V)=
(V)= 

Для двух параллелепипедов


 ;
; 

Мы доказали теорему.
Теорема 2. При АП пространства отношение объемов параллелепипедов сохраняется.
Утверждение. Отношение объемов тел при АП сохраняется.
Представление произвольного АП плоскости
в виде композиции движения и двух сжатий
по взаимно перпендикулярным направлениям.
Теорема. Любое АП плоскости можно представить в виде композиции движения и двух сжатий по взаимно перпендикулярным направлениям.
Лемма. При выполнении произвольного АП плоскости существуют два взаимно перпендикулярных направления плоскости, которое переходит в два взаимно перпендикулярные направления (этой же плоскости).
Доказательство:
Рассмотрим любое АП плоскости А и рассмотрим окружность с центром в т.Р.

Мы знаем, что окружность  эллипс.
эллипс.
Центр окружности т.Р  центр эллипса P’(центр симметрии)
центр эллипса P’(центр симметрии)
Найдем на эллипсе (образе окружности) точку ближайшую к центру Р’, обозначим ее К’
К’Р’ – наименьшее расстояние до точек эллипса.
Пусть при АП А т.К (окр.) → т.К’ (элл.)
Рассмотрим касательную к окружности в т.Р, по свойству касательной она перпендикулярна радиусу РК. Возьмем т.М не принадлежит К на касательной.
При АП А касательная NK→в касательную эллипса.
Доказательство: (от противного)

| Пусть K’N’ не является касательной
К не может перейти в две точки, единственность отображения
У т. N’ нет прообраза => K’N’ – касательная к эллипсу, где K’ – точка касания.
Является ли отрезок K’P’ наименьшим расстоянием до прямой?
Доказательство: (от противного)
Пусть существует L’  | L’P’|<| K’P’|
Но по условию
| L’P’|<| K’P’|
Но по условию  , где Н0 – точка на эллипсе, т.е. по предположению | L’P’|<| Н0P’|, т.е. L’ лежит внутри эллипса => K’N’ – секущая => , где Н0 – точка на эллипсе, т.е. по предположению | L’P’|<| Н0P’|, т.е. L’ лежит внутри эллипса => K’N’ – секущая =>
|

|
=>получаем противоречие => | K’P’| - кратчайшее расстояние от т.P’ до K’N’
Кратчайшее расстояние от P’ до K’N’ измеряется по перпендикуляру =>  => две взаимно перпендикулярных направления найдены.
=> две взаимно перпендикулярных направления найдены.

Доказательство:
Пусть дано АП А плоскости
В качестве начальной СК определяющей данное АП А возьмем ПДСК 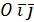 , причем i, j такие векторы, которые при данном АП→ в 2 взаимно
, причем i, j такие векторы, которые при данном АП→ в 2 взаимно  вектора. Такие векторы можно найти в силу леммы.
вектора. Такие векторы можно найти в силу леммы.
Пусть система 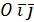


причем  , но
, но  ,
,  ,
, 
Рассмотрим преобразование сжатия ( )
)
 - преобразование, при котором любой вектор
- преобразование, при котором любой вектор  изменяет свою длину в
изменяет свою длину в  раз, соответственно вектор перпендикулярный этому направлению не изменяет свою длину.
раз, соответственно вектор перпендикулярный этому направлению не изменяет свою длину.

 (единичный)
(единичный)


Рассмотрим АП сжатие  , которое переводит
, которое переводит



Рассмотрим композицию АП

 (движение)
(движение)
А преобразование, в котором ПДСК →ПДСК
 (обратное сжатие)
(обратное сжатие)
 - сжатие вдоль вектора
- сжатие вдоль вектора  с коэффициентом
с коэффициентом 
 - сжатие вдоль вектора
- сжатие вдоль вектора  с коэффициентом
с коэффициентом 
А – произведение АП
Теорема. Произвольное АП пространства можно представить в виде композиции некоторого движения пространства и трех сжатий по взаимно перпендикулярны направлениям.
Доказательство: аналогично.