Постановка задачи целочисленного программирования.

По смыслу многих задач требуется, чтобы значения неизвестных в оптимальном плане выражались целыми числами. Это имеет место, когда искомыми величинами являются неделимые объекты: поголовье скота, количество тракторов, тракторных агрегатов, автомашин, комплектов оборудования и т. д.

К обычной формулировке задачи в этих случаях необходимо добавлять условие целочисленности переменных. С таким дополнительным условием получим задачу целочисленного программирования. Она может быть как линейной, так и нелинейной. Рассмотрим решение линейной задачи.

Оптимальный план, найденный обычным симплекс-методом, как правило, не является целочисленным. Простейший выход из положения — округлить полученные результаты до ближайших целых чисел. Однако такое округление во многих случаях дает план, далеко не лучший среди целочисленных планов (т. е. не оптимальный). Иногда простое округление может привести к плану, не удовлетворяющему системе ограничений и, следовательно, вообще непригодному в качестве решения задачи. Особенно часто это бывает, если значения неизвестных выражаются малыми числами. Поэтому для нахождения оптимального целочисленного решения нужен особый алгоритм.

Идея такого алгоритма заключается в следующем. Вначале условие целочисленности не принимается во внимание, и симплекс-методом отыскивается оптимальный план. Если этот план нецелочисленный, составляется дополнительное линейное ограничение, которому удовлетворяет любое целочисленное решение, но заведомо не удовлетворяет найденное. После введения этого ограничения в задачу план становится недопустимым, и решение продолжается опять до получения оптимума. Если новый оптимальный план также окажется нецелочисленным, снова формулируется дополнительное ограничение и для расширенной задачи снова находится оптимум и т. д.

Геометрически дополнительному ограничению соответствует гиперплоскость, которая отсекает от многогранника решений какую-то его часть вместе с полученной нецелочисленной вершиной. При этом все точки с целочисленными координатами остаются в новом многограннике, так что через несколько операций такая точка оказывается на границе и оптимальный план становится целочисленным.

Пусть требуется найти максимум функционала

(1)

при выполнении ограничений:

(2)

Условия неотрицательности переменных могут быть или не быть, но все переменные должны выражаться целыми числами.

Если в системе (2) среди коэффициентов a_i}- и a_t есть дробные числа, то в каждом неравенстве приведем их к общему знаменателю и на этот знаменатель неравенство умножим. От этого смысл неравенства не нарушится, а все коэффициенты станут целыми. Поэтому, не нарушая общности, можно предполагать все коэффициенты системы (2) целыми числами.

Приведем систему ограничений (2) к следующему виду:

(3)

Поскольку в системе (3) все коэффициенты и переменные целочисленны, значения переменных y_i также окажутся целочисленными. Таким образом, целочисленность переменных x_j, независимо от того, будут они исключены из задачи или нет, влечет за собой целочисленность переменных y_t. Преобразованная в случае надобности задача остается задачей целочисленного программирования.

Пусть на переменные x_j наложены условия неотрицательности, т. е. исключения их из задачи не требуется. Составим исходную таблицу и, проделав шагов модифицированных жордановых исключений, найдем оптимальный план (табл. 1). При этом переменных xи у поменяются местами, так что на верху

Таблица 1

	-y1 … -yl -xl+1 … -xn
x1= … xl= yl+1= … ym=	b11 … b1l b1,l+1 … b1n ………………………………………… bl1 … bl bl,l+1 … bln bl+1,1 … bl+1,l bl+1,l+1 … bl+1,n …………………………………………. bm1 … bml bm,l+1 … bmn	b1 ... bl bl+1 ... bm
z=	q1 … ql ql+1 … qn	Q

таблицы и в левом заглавном столбце ее будут стоять переменные обоих видов. По условию оптимальности плана все свободные члены b₁,…,b_m и коэффициенты z-строки q_1,…,q_n будут неотрицательными.

Если в полученной таблице все свободные члены целочисленны, то задача решена. Если же среди них есть хоть один дробный, части решение надо продолжить.

Для удобства, дальнейших рассуждений обозначим все переменные, стоящие в левом заглавном столбце таблицы, символом ( = 1, 2,..., ), а все верхние переменные (j = 1, 2,..., п). Тогда табл. 1 примет несколько иной вид (табл. 2).

Пусть дробным является свободный член b_i. В этой же i-и строке среди коэффициентов b_ij могут быть как целые, так и дробные. Обозначим буквой п с соответствующими индексами наибольшее целое число, не превосходящее данный коэффициент. Так, например, если b_i = 1,7, то n_i = 1; еслиb_i1 = — 1,4, то n_i1 = — 2; если b_i2 = 3, то и n_i2 = 3 и т. д.

Таблица 2

	- 1 … - … - n
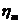= … = … =	b11 … b1j … b1n ………………………………………… bl1 … bij … bin …………………………………………. bm1 … bmj … bmn	b1 ... bi ... bm
z=	q1 … qj … qn	Q

 

Вычтем из каждого коэффициента i-й строки его целую часть, обозначая разность буквой , можем записать

(4)

Если коэффициент b_ijцелый, то n_ij = b_ij и соответствующая разность b_ij равна нулю. Если же b_ij -число дробное, то разность b_ij будет правильной дробью. Поскольку n_ij как для положительных, так и для отрицательных коэффициентов всегда меньше b_ij, разность b_ij-n_ij положительна. Объединяя эти результаты, заключаем, что b_ij будет правильной положительной дробью или нулем. Что же касается разности , то она нулем быть не может, так как b_iне является целым числом:

(5)

В силу условий (5) величина , определяемая формулами (4), называется дробной долей соответствующего числа b. Выпишем из табл. 2 выражение для :

Подставив сюда вместо b_ijи b_i их выражения через целые и дробные части из формул (4), получим

или

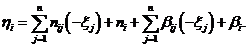(6)

Перепишем равенство (6) в следующем виде:

Обозначим одну из частей буквой s_i:

(7)

Установим, как будет вести себя величина s_i при оговоренных выше условиях.

Если и — целые числа, то в самой правой части выражения (7) будем иметь произведение целых чисел(). Сумма таких произведений есть целое число, к ней алгебраически прибавляется еще два целых числа 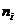и , в итоге получится целое число. Таким образом, величина s_i будет целочисленной.

Поскольку и , в средней части выражения (7) имеем произведения неотрицательных чисел на отрицательные (); отрицательная сумма таких произведений будет положительным числом или нулем. При прибавлении к любому числу (в данном случае к ()) положительного числа результат становится больше:

(от прибавления нулевой суммы результат не изменится, поэтому неравенство нестрогое). Отсюда .

Величина , согласно (5), есть правильная положительная дробь. Точка () на числовой оси расположится между точками (—1) и 0. Исследуемая величина s_i больше, чем (), и в то же время она целочисленна. Но наименьшее целое число, большее (), есть нуль; следовательно, s_i может принимать значения 0, 1, 2, 3 и т. д. Окончательный вывод: при любых целых неотрицательных и величина s_i будет принимать целые неотрицательные значения.

Введем в задачу дополнительное ограничение по первому равенству (7):

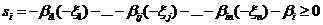(8)

Коэффициентами в этом условии являются взятые с минусом дробные доли соответствующих коэффициентов i-й строки. Расширенную задачу запишем в табл. 3.

Дополнительному ограничению удовлетворяют любые целые неотрицательные и ,т. е. любой целочисленный план задачи.

Таблица 3

	- 1 … - … - n
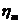= … = … = si=	b11 … b1j … b1n ………………………………………… bl1 … bij … bin …………………………………………. bm1 … bmj … bmn - … - … -	b1 ... bi ... bm
z=	q1 … qj … qn	Q

 

В то же время найденный ранее оптимальный план 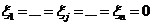для расширенной задачи оказывается недопустимым, так как при этом (иными словами, среди свободных членов появился отрицательный). Этот оптимальный план дополнительным ограничением отсекается, а все целочисленные планы остаются.

Для расширенной задачи обычным путем отыскивается сначала допустимый план, а затем – оптимальный. При использовании на этом этапе двойственного симплекс-метода положительность коэффициентов z-строки не нарушается и объем вычислений сокращается. Если в полученном плане опять окажется дробный свободный член, то по этой строке составляется новое дополнительное ограничение, задача расширяется еще на одно условие и снова находится оптимальный план и т. д.

Так как при целых неотрицательных и будет s_i целое неотрицательное, т. е. ,то существует хотя бы один набор целых , при котором s_i=0. Это говорит о том, что гиперплоскость s_i=0 проходит по крайней мере через одну целочисленную точку. Такая точка может и не принадлежать многограннику. Но целочисленные точки многогранника не отсекаются, и на каком-то этапе сначала одна, а затем и другие дополнительные гиперплоскости пройдут через целочисленную точку, ближайшую к первоначальной оптимальной вершине (рис. 1). Эта точка через конечное число шагов обязательно сама станет оптимальной вершиной. Поэтому можно утверждать, что построенный таким образом алгоритм конечен: через определенное число шагов находится оптимальный целочисленный план, если только такие планы имеются.

Может оказаться, что многогранник решений не будет содержать ни одной целочисленной точки. В этом случае, сколько бы ни вводили дополнительных ограничений, целочисленного допустимого плана получить нельзя. Признаком такого положения, позволяющим избежать ненужных вычислений, является

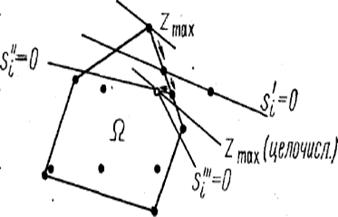
следующий: в какой-либо строке таблицы (кроме, конечно, z-строки) появляется дробный свободный член, а все прочие коэффициенты остаются целыми. Пусть это имеет место для i-й строки табл. 2:

Ясно, что никакими целыми значениями нельзя добиться того, чтобы было целым. Это уравнение в целых числах неразрешимо. Кроме того, если бы захотели по такой строке составить дополнительное ограничение, то все его коэффициенты оказались бы равными нулю. Так как нуль не может быть разрешающим элементом, допустимого плана расширенной задачи отыскать нельзя. Вычисление на этом следует прекратить.

Несовместность исходной системы ограничений устанавливается по обычному критерию на начальной стадии решения задачи.

Теорема:

Целевые функции основной и двойственной задач могут совпадать только для оптимальных планов.

Докажем теорему сначала на примере.

 

§2. Поиск целочисленного решения основной задачи.

Пример.

Доведем до целочисленного решения пример: найти максимум функционала (9) при условиях:

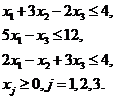(10)

 

(11)

Составляем исходную таблицу и, сделав два шага модифицированных жордановых исключений, приходим к оптимальному плану, записанному в табл. 4.

Таблица 4

	-y3 -y1 -x3
x2= y2= x1=	-1/7 2/7 -1 -15/7 -5/7 -6 3/7 1/7 1	4/7 4/7 16/7
z=	5/7 4/7 4	36/7

 

Полученное оптимальное решение x₁=16/7, x₂=4/7, x₃=0 нецелочисленно,

поэтому приступаем к отысканию целочисленного плана. Проведем его двумя путями: обычным симплекс-методом и двойственным.

Выбираем среди свободных членов дробный. Так как в нашем

примере все они дробные, берем любой из них, например 4/7 из

первой строки. По формулам (4) находим дробные доли коэффициентов b выбранной первой строки:

Дополнительное ограничение будет иметь вид

Вводим это ограничение в задачу и получаем табл.5.

План, записанный в таблице, стал недопустимым. Принимаем за разрешающий элемент число (-2/7), делаем шаг модифицированных жордановых исключений и приходим к таблице 6.

Найденное решение допустимо и целочисленно, но, к сожалению, оно не оптимально. Поэтому выбираем разрешающий элемент (число 3) и делаем следующий шаг (табл.7).

 

 

Таблица 5

	-y3 -y1 -x3
x2= y2= x1= s1=	-1/7 2/7 -1 -15/7 -5/7 -6 3/7 1/7 1 -6/7 -2/7 0	4/7 4/7 16/7 -4/7
z=	5/7 4/7 4	36/7

 

 

Таблица 6

	-y3 -s1 -x3
x2= y2= x1= y1=	-1 1 -1 0 -5/2 -6 0 1/2 1 3 -7/2 0
z=	-1 2 4

 

Теперь решение оптимально, но нарушилась его целочисленность. Берем дробный свободный член 2/3 снова в первой строке и по коэффициентам этой строки формулируем аналогично предыдущему второе дополнительное условие. Практически оно составляется прямо в таблице, поскольку дробные доли коэффициентов легко вычисляются в уме. Записывать их надо со знаком минус (табл.8)

Таблица 7

	-y1 -s1 -x3
x2= y2= x1= y3=	1/3 -1/6 -1 0 -5/2 -6 0 1/2 1 1/3 -7/6 0	2/3 2/3
z=	1/3 5/6 4	14/3

Таблица 8

	-y1 -s1 -x3
x2= y2= x1= y3= s2=	1/3 -1/6 -1 0 -5/2 -6 0 1/2 1 1/3 -7/6 0 -1/3 -5/6 0	2/3 2/3 -2/3
z=	1/3 5/6 4	14/3

 

Чтобы избежать переписывания таблиц, лучше в каждой из них оставлять место под дополнительную строку. Если дополнительное ограничение не потребуется, эта строка останется незаполненной. Зато при необходимости такого условия мы просто впишем его в эту строку таблицы и продолжим решение.

План, записанный в табл. 8, снова является недопустимым.

Выбираем разрешающий элемент (-1/3) и делаем еще один

шаг (табл. 9). План, полученный в табл. 9, является допустимым, оптимальным и целочисленным. Таким образом, нужное решение найдено: x₁=2, x₂=0, x₃=0, z_max=4.

Характерно, что такой план у нас уже был в табл. 6, но там он оказался не оптимальным. Это значит, что с одним дополнительным ограничением в многограннике была еще вершина

Таблица 9

	-s2 -s1 -x3
x2= y2= x1= y3= y1=	1 -1 -1 0 -5/2 -6 0 1/2 1 1 -2 0 -3 5/2 0
z=	1 0 4

 

(2,2/3,0), доставлявшая функционалу большее значение, но

имевшая одну дробную координату. Вторым ограничением эта точка была отсечена, и целочисленная вершина (2, 0, 0) стала оптимальной. Похожий случай представлен на рисунке выше, где движение оптимальной вершины показано стрелками.

Применим теперь для нахождения целочисленного плана двойственный симплекс-метод. Отличия начинаются с табл. 5. Принимаем в ней за разрешающую ту же четвертую строку, но разрешающий элемент в ней определяем двойственными модифицированными отношениями. Они равны

5/7:(-6/7)=-5/6, 4/7:(-2/7)=-2;

меньше по модулю – первое, поэтому за разрешающий принимаем элемент (-6/7). Делая с ним шаг модифицированных исключений, переходим от табл.5 к табл.10.

Таблица 10 тождественна табл. 7, которую мы получили из табл. 5 двумя шагами. Поскольку целочисленный план не найден, составляем по первой строке дополнительное условие и вписываем его в строку s₂ табл. 10. Вычисляем для этой строки двойственные модифицированные отношения

5/6:(-5/6)=-1, 1/3:(-1/3)=-1.

 

Таблица 10

	-s1 -y1 -x3
x2= y2= x1= y3= s2=	-1/6 1/3 -1 -5/2 0 -6 1/2 0 1 -7/6 1/3 0 -5/6 -1/3 0	2/3 2/3 -2/3
z=	5/6 1/3 4	14/3

 

Они равны, но небольшая «прикидка» позволяет установить, что второй столбец за разрешающий принять выгоднее. Делая следующий шаг, получаем табл. 11 (тождественную табл. 9). в которой записан оптимальный целочисленный план. Двойственным симплекс-методом он получен не тремя шагами, а двумя.

Таблица 11

	-s1 -s2 -x3
x2= y2= x1= y3= y1=	-1 -1 -1 -5/2 0 -6 1/2 0 1 -2 1 0 5/2 -3 0
z=	0 1 4